题目
在郊区有 N 座通信基站,P 条 双向 电缆,第 i 条电缆连接基站 Ai 和 Bi。
特别地,1 号基站是通信公司的总站,N 号基站位于一座农场中。
现在,农场主希望对通信线路进行升级,其中升级第 i 条电缆需要花费 Li。
电话公司正在举行优惠活动。
农产主可以指定一条从 1 号基站到 N 号基站的路径,并指定路径上不超过 K 条电缆,由电话公司免费提供升级服务。
农场主只需要支付在该路径上剩余的电缆中,升级价格最贵的那条电缆的花费即可。
求至少用多少钱可以完成升级。
输入格式
第 1 行:三个整数 N,P,K。
第 2..P+1 行:第 i+1 行包含三个整数 Ai,Bi,Li。
输出格式
包含一个整数表示最少花费。
若 1 号基站与 N 号基站之间不存在路径,则输出 −1。
数据范围
0 ≤ K < N ≤ 1000
1 ≤ P ≤ 10000
1 ≤ Li ≤ 1000000
思路
我们可以根据以下样例得到一张图
样例:
5 7 1
1 2 5
3 1 4
2 4 8
3 2 3
5 2 9
3 4 7
4 5 6 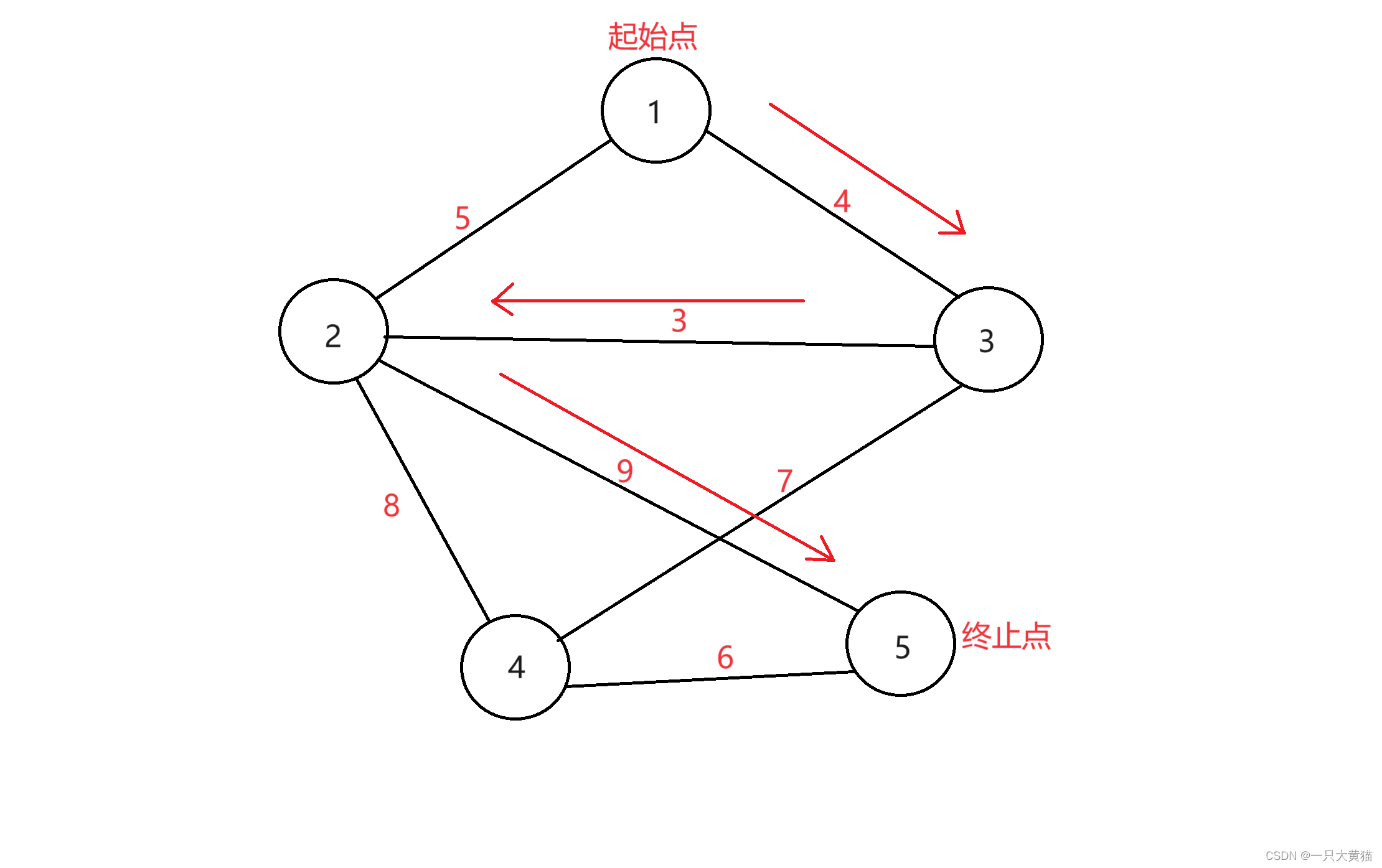
暴力写法,我们可以从0遍历到1000001,找到一个值x:
1、在选择 1 ~ n 的路线中,比这个值x大的边权为 k 个。
2、在满足1条件的 x 集合中,选取最小的那个值。
在寻找最短路的时候,可以将大于 x 的边权当作 1 ,把小于等于 x 的边权当作 0 。
dist数组中储存到当前点经过的大于x的边的个数。
从0~1000001时间复杂度太大,可以使用二分进行优化。
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1010,M = 20010;
typedef pair<int,int> PII;
int n,m,k;// n点数,m边数,k免费电缆数
int h[N],e[M],w[M],ne[M],idx;// 加权邻接表五件套
int dist[N];// 到达第i的点,最少经过多少个超过bound的电缆
bool st[N];// 第i个点的最小值是否已经被确定
void add(int a,int b,int c)
{
e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx ++;
}
bool check(int bound)// 堆优化版dijkstra算法
{
memset(st,0,sizeof(st));// 初始状态,所有点都没有确定最小值
memset(dist,0x3f,sizeof(dist));// 所有点的距离初始为无穷大
dist[1] = 0;// 通信公司的总站为0
priority_queue<PII,vector<PII>,greater<PII>> q;
q.emplace(0,1);
st[1] = true;
while(!q.empty())
{
auto t = q.top();// 取出队头节点,此时该点已经确定为最小值
q.pop();
int x = t.second;
st[x] = false;
for(int i = h[x]; i != -1; i = ne[i])
{
int j = e[i],v = w[i] > bound;// 如果这条边的边权大于bound,则边权为1
if(dist[j] > dist[x] + v)
{
dist[j] = dist[x] + v;
if(!st[j])
{
st[j] = true;
q.emplace(dist[j],j);
}
}
}
}
return dist[n] <= k;
}
int main()
{
cin >> n >> m >> k;// n点数,m边数,k免费电缆数
memset(h,-1,sizeof(h));// 将表头初始化为-1
while(m --)// 输入m条边
{
int a,b,c;
cin >> a >> b >> c;
add(a,b,c),add(b,a,c);// 建立有权值的无向图
}
int l = 0,r = 1e6 + 1;
while(l < r)
{
int mid = (l + r) / 2;
if(check(mid)) r = mid;
else l = mid + 1;
}
if(l == 1e6 + 1) l = -1;
cout << l << endl;
return 0;
}