第四届辽宁省大学生程序设计竞赛（正式赛）（12/13）

news2024/11/26 22:28:34

AC情况

赛中通过赛后通过暂未通过
A√
B√
C√
D○
E○
F√
G√
H√
I○
J√
K—
L√
M√

整体体验

easy：ABFHL

mid：MJGC

hard：IDKE

心得

感觉出了一堆典题，少数题还有些意思，E题确实神仙

题解

A. 欢迎来到辽宁省赛（签到）

输出27

B. 胜率（枚举）

枚举分母到10000

// Problem: 胜率
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/68774/B
// Memory Limit: 524288 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
int t,a,b;
void sol(){
	scanf("%d.%d",&a,&b);
	a=a*100+b;
	//printf("a:%d\n",a);
	//printf("%d\n",30000/7);
	rep(i,1,10000){
		rep(j,0,i){
			int v=j*10000/i,w=(j*100000/i)%10;
			if(w>=5)v++;
			if(v==a){
				pte(i);
				return;
			}
		}
	}
}
int main(){
	t=1;
	while(t--){
		sol();
	}
	return 0;
}
F. 隔板与水槽（枚举）

枚举一下中间的隔板

// Problem: 隔板与水槽
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/68774/F
// Memory Limit: 524288 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
const int N=5e3+10;
int t,n,a[N];
void sol(){
	sci(n);
	rep(i,1,n)sci(a[i]);
	ll ans=0;
	rep(i,2,n-1){
		ll ma=0,mb=0;
		rep(j,1,i-1){
			ma=max(ma,1ll*min(a[i],a[j])*(i-j));
		}
		rep(j,i+1,n){
			mb=max(mb,1ll*min(a[i],a[j])*(j-i));
		}
		ans=max(ans,ma+mb);
	}
	ptlle(ans);
}
int main(){
	t=1;
	while(t--){
		sol();
	}
	return 0;
}
H. 取石子（博弈 性质题）

a^2x^2+ax+1和b^2y^2+by+1都是奇数，所以只和初始局面奇偶性有关

// Problem: 取石子
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/68774/H
// Memory Limit: 524288 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
int t,a,b,n;
void sol(){
	sci(a),sci(b),sci(n);
	puts(n&1?"Alice":"Bob");
}
int main(){
	sci(t); // t=1
	while(t--){
		sol();
	}
	return 0;
}
L. 区间与绝对值（莫队+树状数组）

莫队+树状数组维护增加/删除时对应贡献改变即可

n=q=1e5，4s，O(nsqrt(n)logn)还可以

// Problem: 区间与绝对值
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/68774/L
// Memory Limit: 524288 MB
// Time Limit: 8000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
const int maxn=1e5+10,N=maxn;
int n,m,l,r,a[maxn];
int col[maxn];
int pos[maxn];//pos[i]代表i下标所在的块号
ll now[maxn];//now[i]代表颜色i有几只袜子 
ll res,len,dom,g;
int sz;//块的大小
struct node
{
	int l,r,id;
	ll ans;
}e[maxn];
bool cmp1(node a,node b)
{
	if(pos[a.l]==pos[b.l])
    {
        if(pos[a.l]&1)return a.r>b.r;
        else return a.r<b.r;
    }
	return a.l<b.l;
}
bool cmp2(node a,node b)
{
	return a.id<b.id;
}

struct BitPre{ // 求前缀和(可改为max等)
	int n,tr[N];
	void init(int _n){
		n=_n;
		memset(tr,0,(n+1)*sizeof(*tr));
	}
	void addSum(int x,int v){
		for(int i=x;i<=n;i+=i&-i)
		tr[i]+=v;
	}
	void addMx(int x,int v){
		for(int i=x;i<=n;i+=i&-i)
		tr[i]=max(tr[i],v);
	}
	int askSum(int x){
		int ans=0; 
		for(int i=x;i;i-=i&-i)
		ans+=tr[i];
		return ans;
	}
    int askMx(int x){
		int ans=0; 
		for(int i=x;i;i-=i&-i)
		ans=max(ans,tr[i]);
		return ans;
	}
    // 树状数组求从小到大第k个, 1<=k<=sum(n), 1<=x<=n
    int kth(int k){
        int x=0;
        for(int i=1<<std::__lg(n);i;i>>=1){
            if(x+i<=n && k>tr[x+i]){
                x+=i;
                k-=tr[x];
            }
        }
        return x+1;
    }
}tr,tr2;
void add(int pos,int v){
	res-=tr.askSum(v);
	res+=1ll*tr2.askSum(v)*v;
	res+=tr.askSum(maxn-10)-tr.askSum(v);
	res-=(1ll*tr2.askSum(maxn-10)-tr2.askSum(v))*v;
	tr.addSum(v,v);tr2.addSum(v,1);
}
void del(int pos,int v){
	tr.addSum(v,-v);tr2.addSum(v,-1);
	res+=tr.askSum(v);
	res-=1ll*tr2.askSum(v)*v;
	res-=tr.askSum(maxn-10)-tr.askSum(v);
	res+=(1ll*tr2.askSum(maxn-10)-tr2.askSum(v))*v;
}
signed main(){
	sci(n),sci(m);
	tr.init(maxn-5);
	tr2.init(maxn-5);
	rep(i,1,n)sci(a[i]);
	sz=(int)sqrt(n); 
	for(int i=1;i<=n;++i)
	pos[i]=1+(i-1)/sz;
	for(int i=1;i<=m;++i){
		scanf("%d%d",&e[i].l,&e[i].r);
		e[i].id=i;
	}
	sort(e+1,e+m+1,cmp1);
	l=1;r=0;//[l,r] 初始什么都没有 
	for(int i=1;i<=m;++i){
		for(;r<e[i].r;r++)add(r+1,a[r+1]);
		for(;r>e[i].r;r--)del(r,a[r]);
		for(;l<e[i].l;l++)del(l,a[l]);
		for(;l>e[i].l;l--)add(l-1,a[l-1]);
		e[i].ans=res;
	}
	sort(e+1,e+m+1,cmp2);
	for(int i=1;i<=m;++i){
		printf("%lld\n",2ll*e[i].ans);
	}
	return 0;
}
M. 让二追三（概率期望）

n<5的情况输出0，n>=5的话，统计每个五连位置00111对答案个数的贡献，

有n-4个这样的五连位置，所以是(n-4)*p，其中p为出现00111的概率

// Problem: 让二追三
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/68774/M
// Memory Limit: 524288 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
const int N=1e5+10,mod=1e9+7,inv2=(mod+1)/2;
int t,a,b,n;
int modpow(int x,int n,int mod){
	int res=1;
	for(;n;n>>=1,x=1ll*x*x%mod){
		if(n&1)res=1ll*res*x%mod;
	}
	return res;
}
void sol(){
	sci(a),sci(b),sci(n); 
    if(n<5){
        puts("0");
        return;
    }
	int p=1ll*a*modpow(b,mod-2,mod)%mod;
	int np=(1-p+mod)%mod;
	int w=1ll*p*p%mod*p%mod*np%mod*np%mod;
	pte(1ll*(n-4)*w%mod);
}
int main(){
	sci(t); // t=1
	while(t--){
		sol();
	}
	return 0;
}
J. 齐次递推公约数（反演 gcd fib性质）

类斐波那契数列性质，有f(gcd(i,j))=gcd(f(i),f(j))

所以只需要枚举gcd=d，统计gcd=d的(i,j)对数有多少对，

假设有x对，则对答案的贡献是f(d)*x

可以反演，这里用的是减掉d的倍数的方式，得到恰好等于d的方案数

// Problem: 齐次递推公约数
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/68774/J
// Memory Limit: 524288 MB
// Time Limit: 6000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)]
const int N=3e6+10,mod=1e9+7;
int t,n,f[N],res;
ll cnt[N];
void sol(){
	sci(n);
	f[1]=1;
	rep(i,2,n){
		f[i]=(3ll*f[i-1]%mod+2ll*f[i-2]%mod)%mod;
	}
	per(i,n,1){
		int tot=1;
		for(int j=2*i;j<=n;j+=i){
			cnt[i]-=cnt[j];
			tot++;
		}
		cnt[i]+=1ll*tot*tot;
		res=(res+1ll*cnt[i]%mod*f[i]%mod)%mod;
	}
	pte(res);
	// int res2=0;
	// for(int i=1;i<=n;++i){
		// for(int j=1;j<=n;++j){
			// res2=(res2+__gcd(f[i],f[j]))%mod;
		// }
	// }
	// pte(res2);
}
int main(){
	t=1;
	while(t--){
		sol();
	}
	return 0;
}
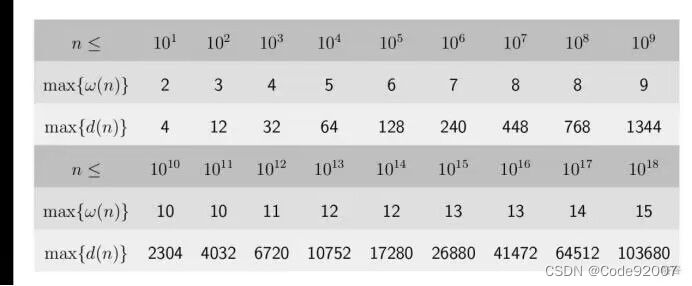
G. 树上公约数（树的直径 ）

枚举gcd=d，将边权是d的倍数的边都连起来，得到对应森林

若森林里存在长度为k的路径，即森林的某棵树上存在长度>=k的直径

对于每棵树两遍搜索求直径，找到符合条件的最大的d，不存在输出-1

复杂度O(n*max(d_{a_{n}}))

// Problem: 树上公约数
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/68774/G
// Memory Limit: 524288 MB
// Time Limit: 10000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
const int N=2e5+10,M=2e5;
int n,k,p[N],w,tmp,to;
vector<int>fac[N],e[N];
vector<int>edg[N];
bool vis[N];
void dfs(int u,int fa,int dis){
	vis[u]=1;
	if(dis>tmp)tmp=dis,to=u;
	for(auto &v:e[u]){
		if(v==fa)continue;
		dfs(v,u,dis+1);
	}
}
int sol(){
	per(i,M,1){
		if(!SZ(edg[i]))continue;
		for(auto &id:edg[i]){
			e[id].clear();
			e[p[id]].clear();
			vis[id]=0;
		}
		for(auto &id:edg[i]){
			e[id].pb(p[id]);
			e[p[id]].pb(id);
		}
		for(auto &id:edg[i]){
			if(vis[id])continue;
			tmp=1;
			dfs(id,0,1);
			tmp=1;
			dfs(to,0,1);
			if(tmp>=k)return i;
		}
	}
	return -1;
}
int main(){
	for(int i=1;i<=M;++i){
		for(int j=i;j<=M;j+=i){
			fac[j].pb(i);
		}
	}
	sci(n),sci(k);
	rep(i,2,n){
		sci(p[i]),sci(w);
		for(auto &d:fac[w]){
			edg[d].pb(i);
		}
	}
	pte(sol());
	return 0;
}
C. 连环爆炸（dp）

题目链接：https://ac.nowcoder.com/acm/contest/68774/C

这个题还挺有意思的，出的挺好的，虽然三个ac的代码都是贪心骗过去的

按怪的先死到后死排序，这样就是无后效性，所以按血量增序排序，

假设我们已经获得了一些预制伤害值就可以顺利触发流程炸死所有怪，

但是不知道这个值具体是多少，所以把这个值存入dp值

按血量增序排序，

dp[i][j]表示前i个怪，手动消灭了j个，令前i个怪全死，还需要在开局预置的伤害数最少是多少

转移就是枚举第i个怪是手动爆的，

还是被前面的崩死的，

还是没崩死，需要开局再补充delta伤害

// Problem: 连环爆炸
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/68774/C
// Memory Limit: 524288 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
const int N=4e3+10;
int n;
P c[N];
ll sum[N],dp[N][N];//dp[i][j]表示前i个手动爆了j个 前i个全死 需要预支的伤害最小值
void ckmin(ll &x,ll y){
	x=min(x,y);
}
int main(){
	sci(n);
	rep(i,1,n)sci(c[i].fi),sci(c[i].se);
	sort(c+1,c+n+1);
	rep(i,1,n){
		rep(j,0,i){
			dp[i][j]=4e18;
		}
	}
	dp[1][0]=c[1].fi;
	dp[1][1]=0;
	sum[1]=c[1].se;
	rep(i,1,n-1){
		sum[i+1]=sum[i]+c[i+1].se;
		rep(j,0,i){
			if(sum[i]<c[i+1].fi){
				ckmin(dp[i+1][j],max(dp[i][j],c[i+1].fi-sum[i]));
			}
			else{
				ckmin(dp[i+1][j],dp[i][j]);
			}
			ckmin(dp[i+1][j+1],max(0ll,dp[i][j]-c[i+1].se));
		}
	}
	// rep(i,1,n){
		// rep(j,0,i){
			// printf("i:%d j:%d dp:%d\n",i,j,dp[i][j]);
		// }
	// }
	rep(i,0,n){
		if(dp[n][i]==0){
			pte(i);
			return 0;
		}
	}
	return 0;
}

补题部分

D. 三角形打野（计算几何 叉积 三分）
题意


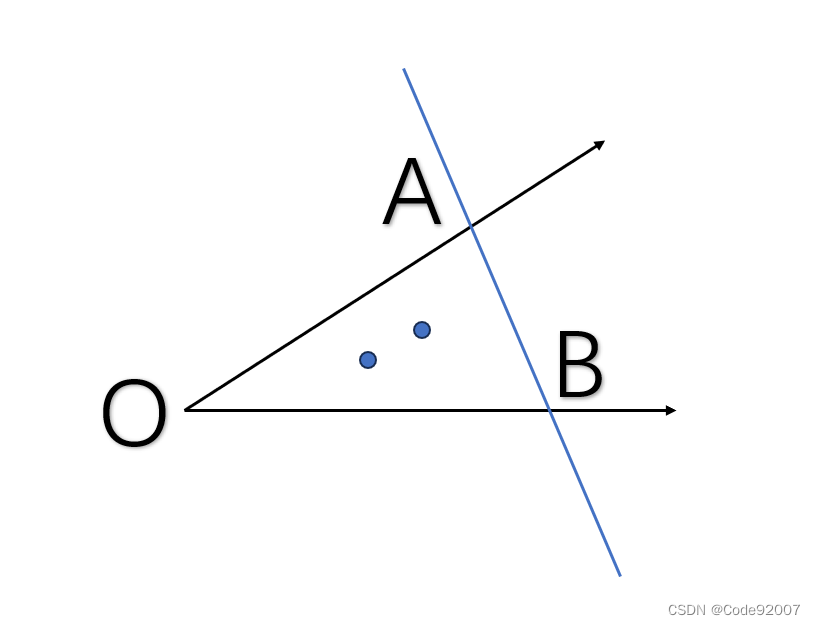
给定x轴正半轴，以及从原点出发的一条射线（在第一象限内），

以及两个点（保证这两个点在给定射线与x正半轴夹角范围内，而不在x轴或给定的射线上），

做一条直线AB，使得这条直线与x正半轴和给定射线组成的三角形将给定的两个点包含在内或边界上。

求满足条件的三角形的最小面积。

两点坐标可能相等，误差小于0.001即为正确

题解

太久不写计算几何感觉基础题都没什么思路，补的话感觉也只能用高中的思路写

手玩一下发现，所求直线AB和x轴的交点是在一个区间内，并且一定过其中至少一个点

记原来给的两个点为P、Q，作PX1平行射线交x轴于X1，作QX2平行射线交x轴于X2

左端点是X1和X2更靠右的那个，右端点可以设成一个很大的值，比如1e18

既然有当前x轴交点坐标，并且能取得最小值，所以凹函数，三分这个x的位置

将当前x轴交点X与P、Q分别连线，XP在XQ顺时针方向说明外侧是XP，否则是XQ

这个也画一下，就很显而易见

然后就是求外侧向量（不妨是XP）与射线的交点，求出交点后用叉积即可求得面积

代码
// Problem: 三角形打野
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/68774/D
// Memory Limit: 524288 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
 
using i64 = long long;
using T = db;
const db eps = 1e-8;
 
struct Point {
    T x;
    T y;
    Point(T x = 0, T y = 0) : x(x), y(y) {}
    
    Point &operator+=(const Point &p) {
        x += p.x, y += p.y;
        return *this;
    }
    Point &operator-=(const Point &p) {
        x -= p.x, y -= p.y;
        return *this;
    }
    Point &operator*=(const T &v) {
        x *= v, y *= v;
        return *this;
    }
    friend Point operator-(const Point &p) {
        return Point(-p.x, -p.y);
    }
    friend Point operator+(Point lhs, const Point &rhs) {
        return lhs += rhs;
    }
    friend Point operator-(Point lhs, const Point &rhs) {
        return lhs -= rhs;
    }
    friend Point operator*(Point lhs, const T &rhs) {
        return lhs *= rhs;
    }
};
 
T dot(const Point &a, const Point &b) {
    return a.x * b.x + a.y * b.y;
}
 
T cross(const Point &a, const Point &b) {
    return a.x * b.y - a.y * b.x;
}
int t;
db k,x,y;
Point a,b;
db pos(db k1,db x,db y){
	db b=y-k1*x;
	return -b/k1;
}
db cal(db z){
	Point p(z,0),o(0,0);
	Point pa=a-p,pb=b-p,pc,po=o-p;
	if(cross(pa,pb)>0)pc=pa;
	else pc=pb;
	if(fabs(pc.x)<eps){
		return 0.5*z*k*z;
	}
	db xs=k*z/(pc.y-k*pc.x);
	Point up(z+xs*pc.x,xs*pc.y);
	pc=up-p;
	db ans=0.5*fabs(cross(pc,po));
	return ans;
}
void sol(){
	scanf("%lf%lf%lf%lf%lf%lf",&y,&x,&a.x,&a.y,&b.x,&b.y);
	db l=0,r=1e18;
	k=y/x;
	l=max(l,pos(k,a.x,a.y));
	l=max(l,pos(k,b.x,b.y));
	while(r-l>eps){
		db m=(l+l+r)/3,m2=(l+r+r)/3;
		if(cal(m)<cal(m2))r=m2;
		else l=m;
	}
	printf("%.10lf\n",cal(l));
}
int main(){
	sci(t); // t=1
	while(t--){
		sol();
	}
	return 0;
}
I. 元-神（单调栈 单调队列）
题意

题解

写到这个题的时间有点不够，感觉再手玩玩就玩出来了，诈骗题

考虑暴力怎么做，最暴力当然是从左往右迭代m^2轮

稍微不那么暴力一点的暴力，是从右到左维护第i个值按时间序都可能是哪些值，是一条链表

但是链表的复杂度也是最坏O(m^2)的，

考虑最右的值只有一种，右数第二的值有两种，以此类推

如果拿第i个值暴力的和第i+1个值的链表上的值一个一个比，自然是O(m^2)的

称第i值为L，第i+1个值的链表上当前要比的值为R

1. 若c[L][R]=1，说明第i个值不会变成这个R，那么第i个值左侧的值有L的阻挡也不会变成R，可以把R从链表里删了

2. 若c[R][L]=1，说明第i个值是L的时候，会在这一轮被同化成R，那么把L加到R的前面，停止操作即可

由于比每次都是从链头比的，并且第i条链是从第i+1条链删掉若干次头结点后塞入元素L，

所以，实际是一个栈结构，单调栈维护即可，就是一个弹栈的过程，

弹到为空或出现第二种情况后，把L放入栈顶，此时栈底的元素就是经过若干轮后最终变成的元素

因为还要访问栈底，所以写的实际是个双端队列

代码
// Problem: 元-神
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/68774/I
// Memory Limit: 524288 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
const int N=1e3+10,M=1e6+10;
int n,t,c[N][N],m,a[M];
int sol(){
	deque<int>q;
	sci(m);
	rep(i,1,m){
		sci(a[i]);
    }
    int ans=0;
    per(i,m,1){
    	while(!q.empty() && !c[q.front()][a[i]])q.pop_front();
    	q.push_front(a[i]);
    	ans^=q.back();
        //printf("%d ",q.back());
    }
	return ans;
}
int main(){
	sci(n);sci(t); // t=1
	rep(i,1,n){
		rep(j,1,n){
			sci(c[i][j]);
		}
	}
	while(t--){
		pte(sol());
	}
	return 0;
}
E. 神-原（lucas定理 递归 极值点）
题目

思路来源

2023辽宁省赛E-CSDN博客

题解

纯纯神仙题，完全根据思路来源补的代码

虽然lucas的部分是暴力展开的，但是我极值取到的[l,r]就没求出来

虽然理论复杂度在p=2这是1e7左右，但是写的时候是瓶颈，实际提交的过程中一度TLE

最后想起来，p=2的时候，lucas定理的推论，n&m=m时C(n,m)%p=1，

加上之后就AC了，那一刻，真香！

代码
// Problem: 神-原
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/68774/E
// Memory Limit: 524288 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef unsigned long long ull;
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
const int N=1e6+10,M=1e6,H=2e7+10;
int n,m,p,mod;
int Finv[N],fib[N],fac[N],inv[N];
int f(int a,int n);
int g(int a,int n);
int modpow(int x,int n,int mod){
	int res=1;
	for(;n;x=1ll*x*x%mod,n>>=1)
	if(n&1)res=1ll*res*x%mod;
	return res;
}
void init(int n){ //n<N
    inv[0]=inv[1]=1;
    fib[0]=0;fib[1]=1;
    rep(i,2,n)fib[i]=(fib[i-1]+fib[i-2])%mod;
    for(int i=2;i<=n;++i)inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
	fac[0]=Finv[0]=1;
	for(int i=1;i<=n;++i)fac[i]=1ll*fac[i-1]*i%mod,Finv[i]=1ll*Finv[i-1]*inv[i]%mod;
}
int C(int n,int m){
	if(m<0||m>n)return 0;
    if(p==2)return (n&m)==m?1:0;
	int ans=1ll*fac[n]*Finv[n-m]%mod*Finv[m]%mod;
	//printf("n:%d m:%d c:%d\n",n,m,ans);
	return ans;
}
int Lucas(int n, int m){
  if(m<0||m>n)return 0;
  if(p==2)return (n&m)==m?1:0;
  return m==0?1:1ll*C(n%p,m%p)*Lucas(n/p,m/p)%p;
}
int g(int a,int n){
    //if(a<0 || n<0)return 0;
    int x=n%p,y=n/p,z=a/p;
	int v=1ll*f(x,x)*f(z-1,y)%p;
	if(p-1==x)return v;
	int w=(f(p-1,x+p)-f(x,x+p)+p)%p;
    if(w){
        int u=f(z-1,y-1);
	    v=(v+1ll*w*u%p)%p;
    }
	return v;
}
int ch(int a,int n){
	int up=a%p,ans=0;
	rep(i,0,up){
		int l=C((n-i)%p,i),r=Lucas((n-i)/p-a/p,a/p);
		ans=(ans+1ll*l*r%p)%p;
	}
	return ans;
}
int f(int a,int n){
    if(a<0 || n<0)return 0;
    if(a==n && n<M)return fib[n+1];
	a=min(a,n);
    if(n<=p){
        int ans=0;
		rep(i,0,a){
			ans=(ans+C(n-i,i))%mod;
		}
		//printf("a:%d n:%d ans:%d\n",a,n,ans);
		return ans;
    }
	if(a<=M){
		int ans=0;
		rep(i,0,a){
			ans=(ans+Lucas(n-i,i))%mod;
		}
		//printf("a:%d n:%d ans:%d\n",a,n,ans);
		return ans;
	}
	return (g(a,n)+ch(a,n))%p;
}
int sol(){
	if(!m)return f(n-1,n-1);
    if(m==n)return 0;
	int l=(n-2*m+2)/3+1,r=l+m-1;
	if(l<1)l=1,r=m;
	//printf("l:%d r:%d f(n-1,n-1):%d\n",l,r,f(n-1,n-1));
	int v=(f(n-1,n-1)-f(r-1,n-1)+p)%p;
	if(l>1)v=(v+f(l-2,n-m-1))%p;
	return v;
}
int main(){
	sci(n),sci(m),sci(p);
	mod=p;
	init(M);
	pte(sol());
	return 0;
}
K. 稻妻扑克（大模拟）

大模拟，咕咕咕

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1175651.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

bff层解决了什么痛点

bff层解决了什么痛点

bff层 -- 服务于前端的后端 什么是bff&#xff1f; Backend For Frontend&#xff08;服务于前端的后端&#xff09;&#xff0c;也就是服务器设计API的时候会考虑前端的使用&#xff0c;并在服务端直接进行业务逻辑的处理&#xff0c;又称为用户体验适配器。BFF只是一种逻辑…
阅读更多...
基于爬行动物算法的无人机航迹规划-附代码

基于爬行动物算法的无人机航迹规划-附代码

基于爬行动物算法的无人机航迹规划 文章目录 基于爬行动物算法的无人机航迹规划1.爬行动物搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要&#xff1a;本文主要介绍利用爬行动物算法来优化无人机航迹规划。 …
阅读更多...
Python|OpenCV-图像的添加和混合操作(8)

Python|OpenCV-图像的添加和混合操作(8)

前言 本文是该专栏的第8篇，后面将持续分享OpenCV计算机视觉的干货知识，记得关注。 在使用OpenCV库对图像操作的时候，有时需要对图像进行运算操作，类似于加法，减法，位操作等处理。而本文，笔者将针对OpenCV对图像的添加，混合以及位操作进行详细的介绍说明和使用。 下面，…
阅读更多...
03、SpringBoot + 微信支付 ---- 创建订单、保存二维码url、显示订单列表

03、SpringBoot + 微信支付 ---- 创建订单、保存二维码url、显示订单列表

目录 Native 下单1、创建课程订单保存到数据库1-1&#xff1a;需求&#xff1a;1-2&#xff1a;代码&#xff1a;1-3&#xff1a;测试结果&#xff1a; 2、保存支付二维码的url2-1&#xff1a;需求&#xff1a;2-2&#xff1a;代码&#xff1a;2-3&#xff1a;测试&#xff1a;…
阅读更多...
python 之 sorted 函数

python 之 sorted 函数

文章目录 sorted() 函数的语法返回值使用示例&#xff1a;示例 1&#xff1a;基本使用示例 2&#xff1a;指定降序排序示例 3&#xff1a;使用 key 参数进行自定义排序 注意事项&#xff1a; sorted() 是 Python 中的一个内置函数&#xff0c;用于对可迭代对象进行排序&#xf…
阅读更多...
jquery之checkbox全选反选提交参数

jquery之checkbox全选反选提交参数

实现效果 <!DOCTYPE html> <html> <head><meta charset"UTF-8"><title>Checkbox操作示例</title><script src"https://code.jquery.com/jquery-3.5.1.min.js"></script><script>$(document).ready(…
阅读更多...
FPGA高端项目：图像缩放+GTP+UDP架构，高速接口以太网视频传输，提供2套工程源码加QT上位机源码和技术支持

FPGA高端项目：图像缩放+GTP+UDP架构，高速接口以太网视频传输，提供2套工程源码加QT上位机源码和技术支持

目录 1、前言免责声明本项目特点 2、相关方案推荐我这里已有的 GT 高速接口解决方案我这里已有的以太网方案我这里已有的图像处理方案 3、设计思路框架设计框图视频源选择ADV7611 解码芯片配置及采集动态彩条跨时钟FIFO图像缩放模块详解设计框图代码框图2种插值算法的整合与选择…
阅读更多...
【数据结构与算法】JavaScript实现哈希表

【数据结构与算法】JavaScript实现哈希表

文章目录 一、哈希表简介1.1.认识哈希表1.2.哈希化的方式1.3.解决冲突的方法1.4.寻找空白单元格的方式线性探测二次探测再哈希化 1.5.不同探测方式性能的比较1.6.优秀的哈希函数快速计算均匀分布 二、初步封装哈希表2.1.哈希函数的简单实现2.2.创建哈希表2.3.put(key,value)2.4…
阅读更多...
时间序列预测模型实战案例(七)(TPA-LSTM)结合TPA注意力机制的LSTM实现多元预测

时间序列预测模型实战案例(七)(TPA-LSTM)结合TPA注意力机制的LSTM实现多元预测

论文地址->TPA-LSTM论文地址 项目地址-> TPA-LSTM时间序列预测实战案例 本文介绍 本文通过实战案例讲解TPA-LSTM实现多元时间序列预测&#xff0c;在本文中所提到的TPA和LSTM分别是注意力机制和深度学习模型,通过将其结合到一起实现时间序列的预测&#xff0c;本文利用…
阅读更多...
Google发布移动终端对象检测模型——mediapipe，无GPU依然飞快

Google发布移动终端对象检测模型——mediapipe，无GPU依然飞快

对象检测模型最出名的当选YOLO系列，其YOLO系列已经更新到V8系列，但是现有的YOLO模型面临限制，如量化支持不足和准确性延迟权衡不足。 YOLO-NAS模型在包括COCO、Objects365和Roboflow 100在内的知名数据集上进行了预训练，使其非常适合生产环境中的下游对象检测任务。YOLO-NA…
阅读更多...
unity【动画】脚本_角色动画控制器 c#

unity【动画】脚本_角色动画控制器 c#

首先创建一个代码文件夹Scripts 从人物角色Player的基类开始 创建IPlayer类 首先我们考虑到如果不挂载MonoBehaviour需要将角色设置成预制体实例化到场景上十分麻烦&#xff0c; 所以我们采用继承MonoBehaviour类的角色基类方法写代码 也就是说这个脚本直接绑定在角色物体…
阅读更多...
Quartz之JDBC-JobStoreTX配置

Quartz之JDBC-JobStoreTX配置

一、前言 上篇 《Quartz介绍》中使用的是RAMJobStored存储调度信息&#xff0c;当进程终止调度信息会丢失&#xff0c;本篇我们介绍使用JDBCJobStore来存储调度信息&#xff08;jobs、Triggers和日历&#xff09;。 二、Quartz 表结构 可以从官网&#xff08;http://www.qua…
阅读更多...
康耐视深度学习ViDi-ViDi四大工具介绍与主要用途

康耐视深度学习ViDi-ViDi四大工具介绍与主要用途

Cognex ViDi 工具是一系列机器视觉工具&#xff0c;通过深度学习解决各种难以解决的挑战。虽然这些工具共享一个引擎&#xff0c;但它们在图像中寻找的内容不同。更具体地说&#xff0c;在分析单个点、单个区域或完整图像时&#xff0c;每个工具都有不同的侧重点。 Locate&…
阅读更多...
JUC并发编程系列(一)：Java线程

JUC并发编程系列(一)：Java线程

前言 JUC并发编程是Java程序猿必备的知识技能&#xff0c;只有深入理解并发过程中的一些原则、概念以及相应源码原理才能更好的理解软件开发的流程。在这篇文章中荔枝会梳理并发编程的基础&#xff0c;整理有关Java线程以及线程死锁的知识&#xff0c;希望能够帮助到有需要的小…
阅读更多...
30、JAVA进阶——Socket编程

30、JAVA进阶——Socket编程

✅作者简介：热爱国学的Java后端开发者，修心和技术同步精进。 🍎个人主页：乐趣国学的博客 🍊个人信条：不迁怒，不贰过。小知识，大智慧。 💞当前专栏：JAVA开发者成长之路 ✨特色专栏：国学周更-心性养成之路 🥭本文内容：JAVA进阶——Socket编程 更多内容点击👇 …
阅读更多...
idea2023 PoJie以后无法修改内存无效

idea2023 PoJie以后无法修改内存无效

1. 打开电脑环境变量 2. 找到对应pojie文件 vmoptions目录 3. 修改这个文件 添加或者修改配置 -Xms128m -Xmx8192m4. 重启idea 修改成功
阅读更多...
flutter开发报错The instance member ‘widget‘ can‘t be accessed in an initializer

flutter开发报错The instance member ‘widget‘ can‘t be accessed in an initializer

文章目录 问题描述问题原因解决方法 问题描述 The instance member ‘widget’ can’t be accessed in an initializer. 问题原因 “The instance member ‘widget’ can’t be accessed in an initializer” 错误是因为在初始化器列表中&#xff08;constructor initializer…
阅读更多...
JavaScript使用正则表达式

JavaScript使用正则表达式

正则表达式(RegExp)也称规则表达式(regular expression)&#xff0c;是非常强大的字符串操作工具&#xff0c;语法格式为一组特殊字符构成的匹配模式&#xff0c;用来匹配字符串。ECMAScript 3以Perl为基础规范JavaScript正则表达式&#xff0c;实现Perl 5正则表达式的子集。Ja…
阅读更多...
Linux常用命令——cdrecord命令

Linux常用命令——cdrecord命令

在线Linux命令查询工具 cdrecord Linux系统下光盘刻录功能命令 补充说明 cdrecord命令用于Linux系统下光盘刻录&#xff0c;它支持cd和DVD格式。linux下一般都带有cdrecord软件。 语法 cdrecord(选项)(参数)选项 -v&#xff1a;显示刻录光盘的详细过程&#xff1b; -eje…
阅读更多...
基于社交网络算法的无人机航迹规划-附代码

基于社交网络算法的无人机航迹规划-附代码

基于社交网络算法的无人机航迹规划 文章目录 基于社交网络算法的无人机航迹规划1.社交网络搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要&#xff1a;本文主要介绍利用社交网络算法来优化无人机航迹规划。 …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023