给出一个非负的整数x，返回x的平方根向下取整的结果，这个被返回的数也应该是一个非负的值。
对我们的要求是不能使用任何内置的指数函数与操作，官方还给了我们例子：
在C++种不能使用pow(x, 0.5) 在python不能使用 x**0.5
既然官方已经这样要求了，那么我们就不使用这些操作了.
我最先的思路是这样的从0开始进行枚举，00与x进行比较，如果00小于x，就向后比较11与x的关系，当依次增大直到不符合条件，因为我们设置的是mm<x 则继续进行比较，但是现在mm>=x，所以我们还需要进行判断mm是大于x还是等于x，当大于x时，说明m-1是答案，当等于x时说明m是答案。

int mySqrt(int x){
    int i = 0;
    for(;i<=x/2;i++){
        if(i*i>=x){
            break;
        }
    }
    if(i*i==x){
        return i;
    }
    return i-1;
}

但是这一种方式太过于耗费时间了，因为它从0开始进行枚举，这样就太过多了其实如果能建立二叉树就能以O(logn)的时间复杂度进行平方根的查找。我们这一次不用二叉树进行查找，我是用两个变量记录查询的上下界，这样不断的进行将查询区间进行二分，最终也能实现O(logn)时间复杂度。这一个问题其实是一个二分查找的问题。

int sqrt(int x){
    int left = 0;
    int right = x;
    int middle = (left+right)/2;
    while(left<right){
        if(middle*middle<x){
            left = middle+1;
        }else if(middle*middle>x){
            right = middle - 1;
        }else{
            return middle;  // 如果是整数之一，就会直接返回，而不会跳出循环，如果跳出循环，说明只有一个近似的根，无整数平方根
        }
        middle = (right + left)/2; 
    }
    return right; // 从循环跳出这一种情况，数x的平方根取整后一定是right，这一个可以自行验证
}

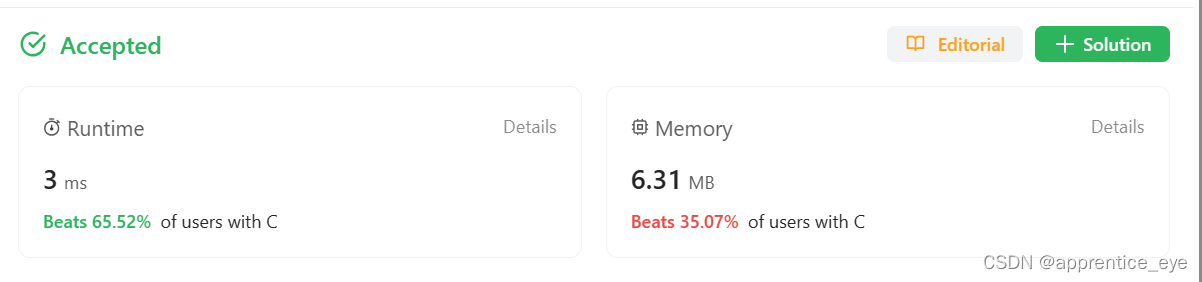
运行结果截图：