大家好我是苏麟 , 今天说说数的层序遍历 .

层次遍历简介

广度优先在面试里出现的频率非常高，整体属于简单题，但是很多人面试遇到时就直接放弃了，实在可惜。我们本章就集中研究一下到底难在哪里。

广度优先又叫层次遍历，基本过程如下 :

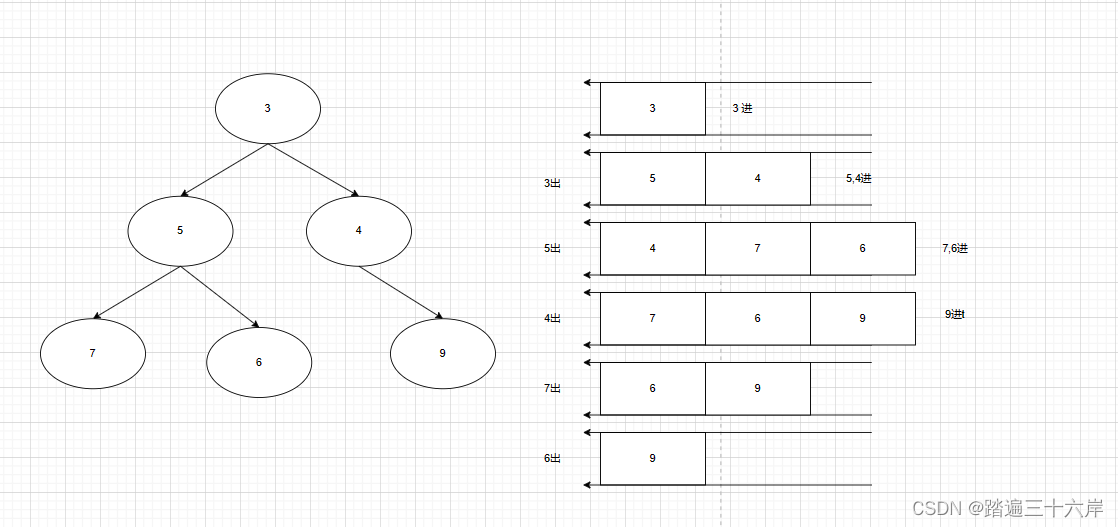
层次遍历就是从根节点开始，先访问根节点下面一层全部元素，再访问之后的层次，类似金字塔一样一层层访问。我们可以看到这里就是从左到右一层一层的去遍历二叉树，先访问3，之后访问3的左右子孩子5和4，之后分别访问5 和4的左右子孩子[7,6]和[9]，最后得到结果[3,5,4,7,6,9]。

这里的问题是怎么将遍历过的元素的子孩子保存一下呢，使用队列来存储能完美解决上述问题，例如上面的图中:

首先3入队。
然后3出队，之后将3的左右子孩子5和4 保存到队列中。
之后5出队，将5的左右子孩子7和6入队
之后4出队，将4的右子孩子9入队。
之后 7,6,9分别出队，此时都是叶子结点，只出队就行了

该过程不复杂 . 

基本的层次遍历

最简单的层次遍历

我们先看最简单的情况，仅仅遍历并输出全部元素，如下 : 

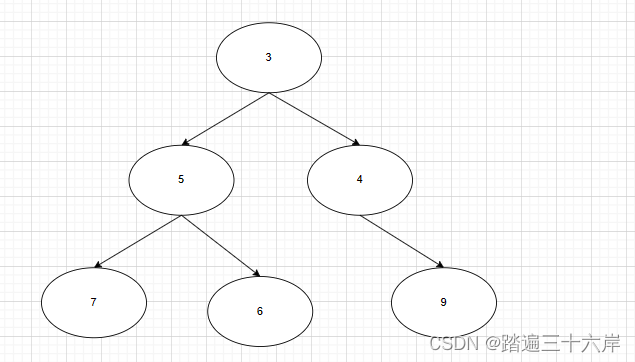
上面的二叉树应输出结果 [3,5,4,7,6,9]，方法上面已经图示了，这里看一下怎么代码实现 ?

List<Integer> simpleTree(TreeNode treeNode){
    //空则返回
    if(treeNode == null){
        return new ArrayList<>();
    }

    //存放数字
    List<Ineteger> list = new ArrayList<>();

    //存放节点
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(treeNode);

    while(queue.size() > 0){
        TreeNode temp = queue.remove();
        list.add(temp.val);
        
        if(temp.left != null){
            queue.add(temp.left);
        }
        if(temp.left != null){
            queue.add(temp.right);
        }
    }

    return list;
}

根据树的结构可以看到，一个结点在一层访问之后，其子孩子都是在下层按照FIFO的顺序处理的，因此队列就是一个缓存的作用。

这期就到这里 , 下一关见!