引入平衡树
假设我们有两个节点：
当我们插入第三个节点，就失衡了：
此刻我们就要把它平衡一下。
为什么要变平衡
为什么说它失衡了呢，又为什么要把它变平衡？
如图a，假设我们要查找30这个节点就要查3次才能找到
但是如果平衡之后(图b）就只需要2次就可以找到了，这样可以提高效率，这两个图不够明显，如果是100个节点的图就够明显了。
怎么判断是否需要变平衡
我们引入 平衡因子的概念
平衡因子 = 根节点的 左孩子高度 - 右孩子高度
当 平衡因子的绝对值 > 1 时，我们认为这个树是失衡的，需要变为平衡。
如图(c-1）：
根节点( 10 ) 的左孩子高度（0） - 右孩子高度（2）= 平衡因子 （-2）
| -2 | > 1，即该数树为失衡的树。
怎么变平衡
首先，假如有这样一个二叉搜索树：
LL型失衡
我们应该怎么平衡呢？
首先，因为根节点最小，所以把根节点变到2的右边，这也符合二叉搜索的特性，即：小了往左走
这个时候20就成了新的根节点，而原先的根节点10就成了现在根节点（20）的左孩子节点。
因此对于这种一边倒的二叉搜索树，并且是向左倒的：
也就是要往左边分点节点，我们才能保持它的平衡，
对于LL型失衡，我们可以总结有如下 左旋定理:
RR型失衡
同理，有往左边倒的就有往右边倒的，如下图:
因为40比30大的缘故，我们可以让40到30的右边去，这样就平衡了，并且符合二叉搜索树的特性，即:大了就往右边走:
此时30就是新节点，40就为30的右孩子。
这种往右边一边倒的失衡，我们称之为RR型失衡。
对此，我们可以总结如下右旋定理:
LR型失衡
因为root节点的左孩子的右节点造成的失衡就叫LR型失衡，如图 (b-1)：
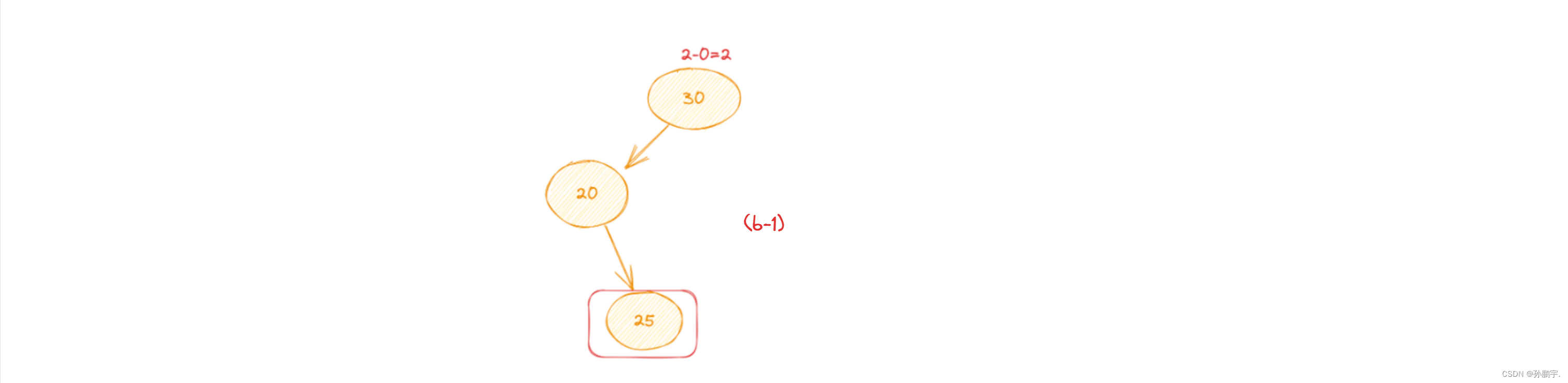
因为是由于右节点造成的失衡，所以我们就让右节点到左节点去，可以用左旋定理：
变为图 （b-2）: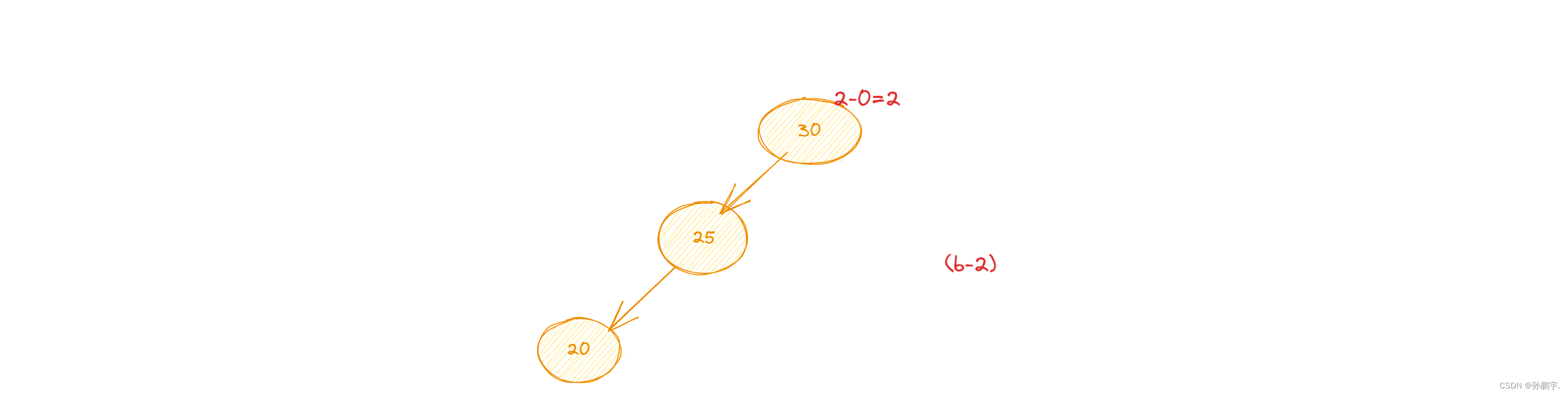
图(b-2)我们看它的平衡因子，大于1，所以还要再变。
又因为图(b-2）是RR型失衡，所以套用 右旋定理：
变为图（b-3）:
此时平衡因子<1，是AVL树，因此不再变。
流程图：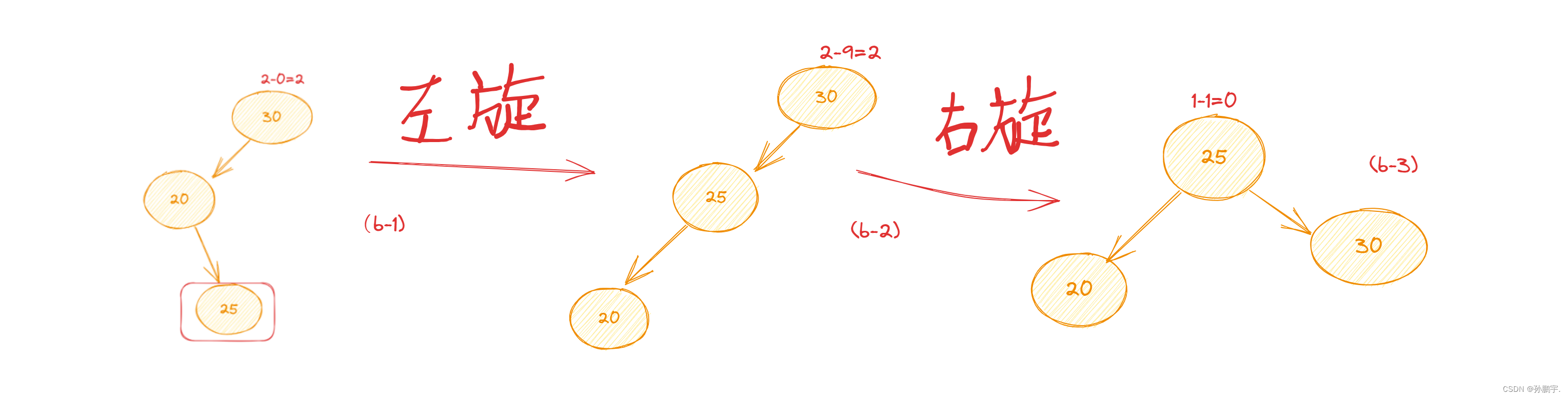
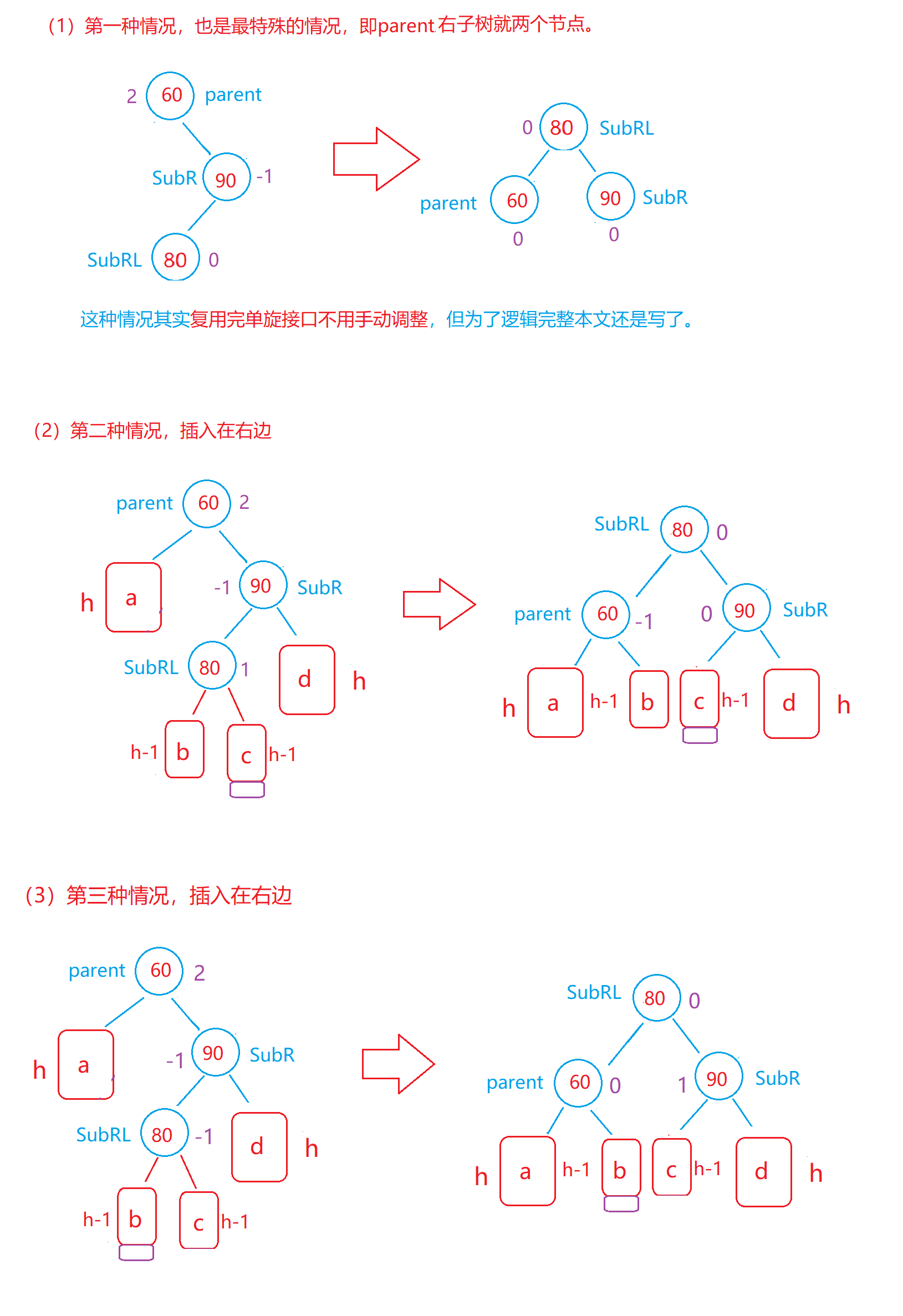
RL型失衡
如图（a-1），因为root节点的右孩子的左节点造成的失衡就叫RL型失衡：
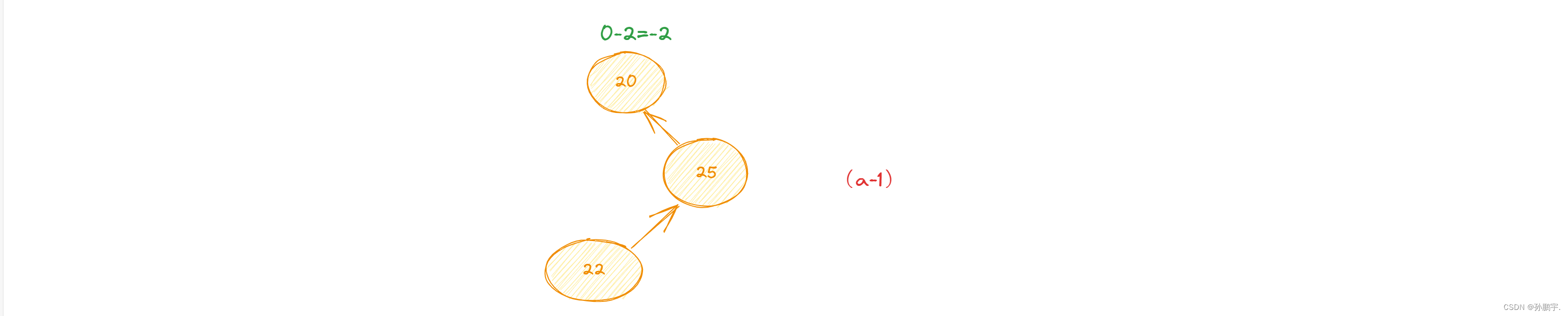对于LR型失衡，因为是左节点造成的失衡，所以要先采用右旋定理把右节点变到左边去：
变为图（a-2）：
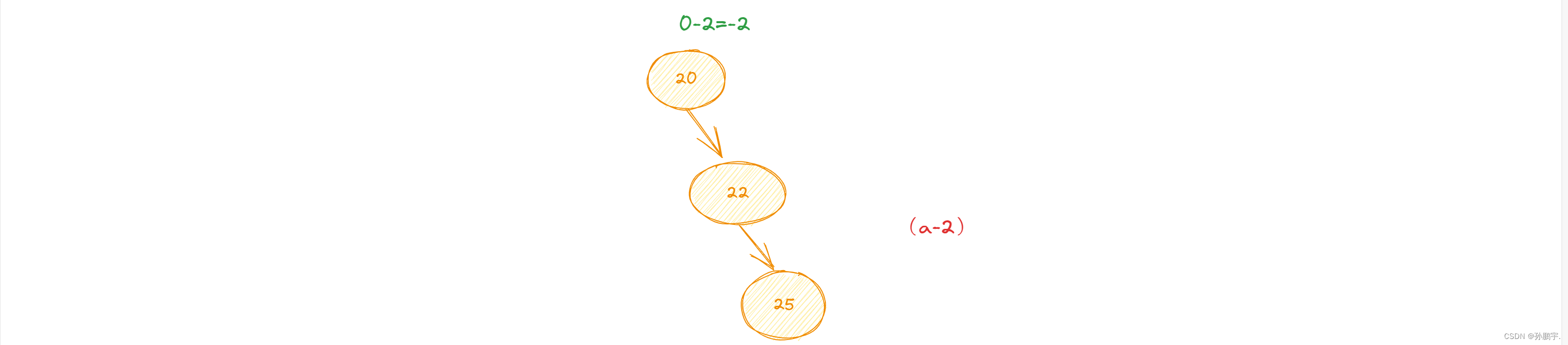此时平衡因子为 -2 ，仍然不平衡还需要再变
此时因为向左倾斜，即要向左部分分点，这样才平衡要调用 左旋定理 ：
变为图 （a-3）：
此时平衡因子 <1,即不用再变。
流程图: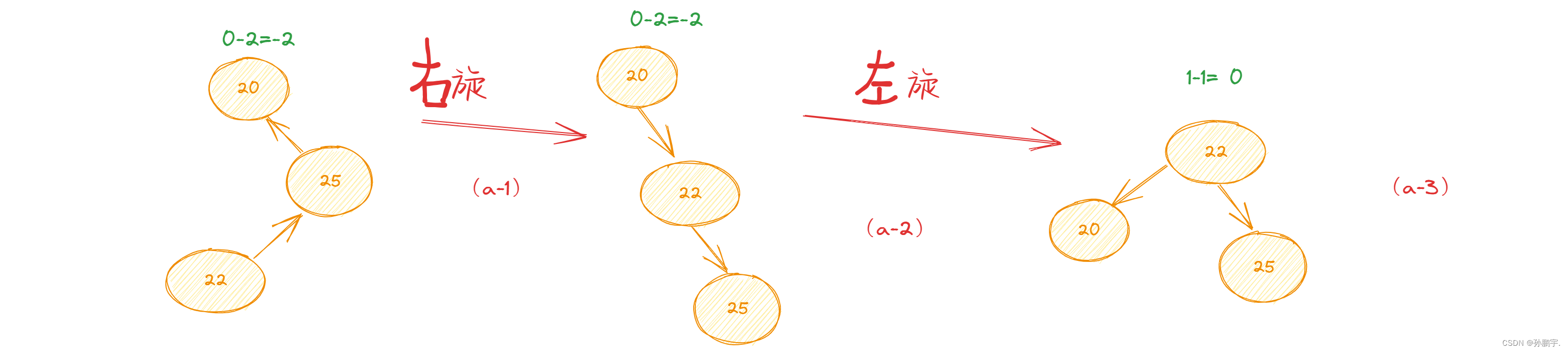
Code
首先写一下树的结构
val left right是必须的，又新加了一个height，用来求平衡因子用:
typedef struct Node
{
int val;//数据域
int height; //树高
struct Node* left;
struct Node* right;
}Node;开辟一个新节点:
Node* newnode = (Node*)malloc(sizeof(Node));初始化：
node->val=val;
node->height = 1;
node->left = NULL;
node->right = NULL;开辟和初始化我们都封装起来:
Node* Init(int val)
{
Node* node = (Node*)malloc(sizeof(Node));
node->val=val;
node->height = 1;
node->left = NULL;
node->right = NULL;
}
