文章目录
- 5.1 树的基本概念
- 5.1.1 树的定义
- 5.1.2 森林的定义
- 5.1.3 树的术语
- 5.1.4 树的表示
- 1.树形表示法
- 2.嵌套集合表示法
- 结构体
- 创建树
- 主函数
- 3.嵌套括号表示法
- 结构体
- 创建树
- 嵌套括号表示法
- 主函数
- 4.凹入表示法
- 结构体
- 创建树
- 凹入表示法
- 主函数
5.1 树的基本概念
5.1.1 树的定义
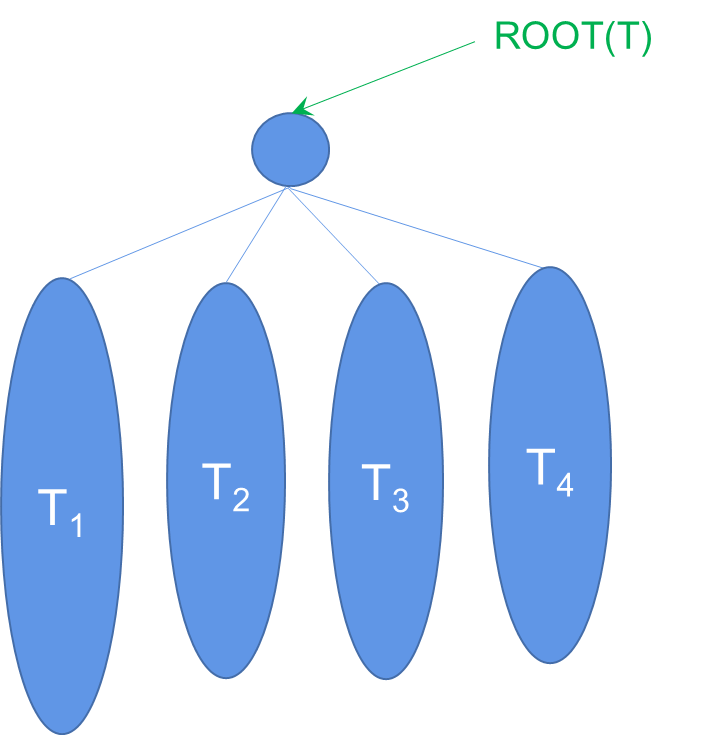
- 一棵树是结点的有限集合T:
- 若T非空,则:
- 有一个特别标出的结点,称作该树的根,记为root(T);
- 其余结点分成若干个不相交的非空集合T1, T2, …, Tm (m>0),其中T1, T2, …, Tm又都是树,称作root(T)的子树。
- T 空时为空树,记作root(T)=NULL。
- 若T非空,则:
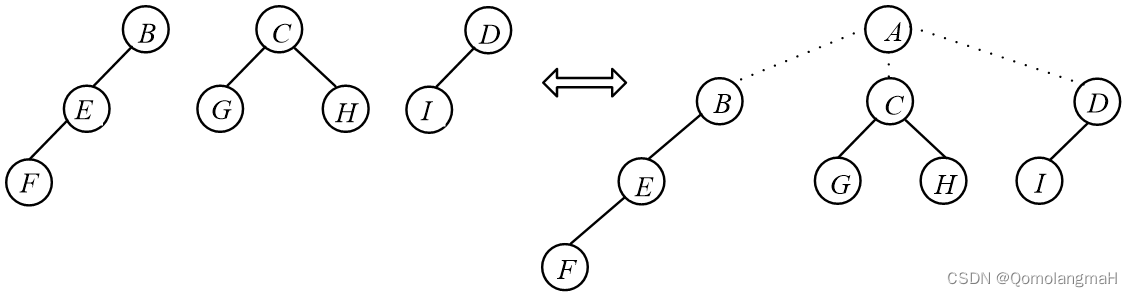
5.1.2 森林的定义
一个森林是0棵或多棵不相交(非空)树的集合,通常是一个有序的集合。换句话说,森林由多个树组成,这些树之间没有交集,且可以按照一定的次序排列。在森林中,每棵树都是独立的,具有根节点和子树,树与树之间没有直接的连接关系。
森林是树的扩展概念,它是由多个树组成的集合。在计算机科学中,森林也被广泛应用于数据结构和算法设计中,特别是在图论和网络分析等领域。
5.1.3 树的术语
- 父亲(parent)、儿子(child)、兄弟(sibling)、后裔(descendant)、祖先(ancestor)
- 度(degree)、叶子节点(leaf node)、分支节点(internal node)
- 结点的层数
- 路径、路径长度、结点的深度、树的深度
参照前文:【数据结构】树与二叉树(一):树(森林)的基本概念:父亲、儿子、兄弟、后裔、祖先、度、叶子结点、分支结点、结点的层数、路径、路径长度、结点的深度、树的深度
5.1.4 树的表示
1.树形表示法
树形表示法是一种图形化的表示方法,使用节点和边来表示树的结构。每个节点代表树中的一个元素,而边表示节点之间的关系。这种表示方法可以直观地展示树的层次结构和节点之间的连接关系。
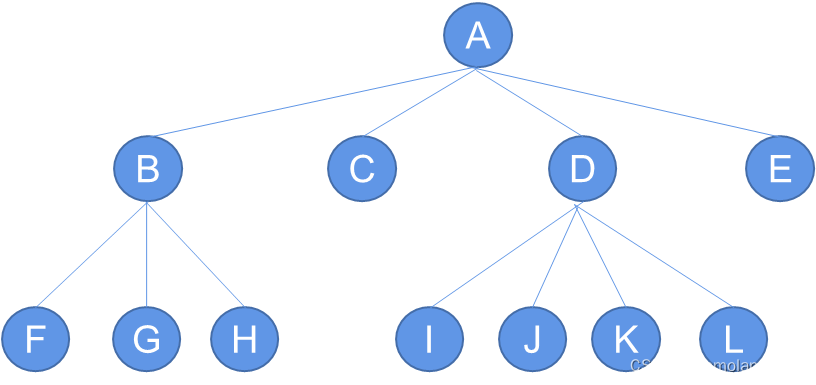
2.嵌套集合表示法
嵌套集合表示法使用集合的嵌套结构来表示树:每个集合代表一个节点,而集合中的元素表示该节点的子节点。通过嵌套的方式,可以表示出树的层次结构。
tree = {
'value': 'A',
'children': [
{
'value': 'B',
'children': []
},
{
'value': 'C',
'children': [
{
'value': 'D',
'children': []
}
]
}
]
}
结构体
#include <stdio.h>
#include <stdlib.h>
struct TreeNode {
int value;
struct TreeNode** children;
int numChildren;
};
创建树
struct TreeNode* createTreeNode(int value, int numChildren) {
struct TreeNode* node = (struct TreeNode*)malloc(sizeof(struct TreeNode));
node->value = value;
node->numChildren = numChildren;
node->children = (struct TreeNode**)malloc(numChildren * sizeof(struct TreeNode*));
for (int i = 0; i < numChildren; i++) {
node->children[i] = NULL;
}
return node;
}
主函数
int main() {
struct TreeNode* root = createTreeNode(1, 2);
struct TreeNode* node1 = createTreeNode(2, 0);
struct TreeNode* node2 = createTreeNode(3, 1);
struct TreeNode* node3 = createTreeNode(4, 0);
root->children[0] = node1;
root->children[1] = node2;
node2->children[0] = node3;
// 其他操作...
return 0;
}
3.嵌套括号表示法
嵌套括号表示法使用括号来表示树的结构:每对括号代表一个节点,而括号内的内容表示该节点的子节点。通过嵌套括号的方式,可以清晰地表示树的层次结构和节点之间的关系。
tree_str = '((A (B C)) D)'
结构体
#include <stdio.h>
#include <stdlib.h>
struct TreeNode {
int value;
struct TreeNode* left;
struct TreeNode* right;
};
创建树
struct TreeNode* createTreeNode(int value) {
struct TreeNode* node = (struct TreeNode*)malloc(sizeof(struct TreeNode));
node->value = value;
node->left = NULL;
node->right = NULL;
return node;
}
嵌套括号表示法
// 根据嵌套括号表示法构建树
struct TreeNode* buildTreeFromParenthesis(char* treeStr, int* index) {
struct TreeNode* node = NULL;
int value = 0;
int sign = 1;
while (treeStr[*index] != '\0') {
char c = treeStr[*index];
(*index)++;
if (c == '(') {
if (node == NULL) {
node = (struct TreeNode*)malloc(sizeof(struct TreeNode));
node->left = NULL;
node->right = NULL;
}
node->left = buildTreeFromParenthesis(treeStr, index);
} else if (c == ')') {
return node;
} else if (c == '-') {
sign = -1;
} else if (c >= '0' && c <= '9') {
value = value * 10 + (c - '0');
} else if (c == ' ') {
value *= sign;
node->value = value;
value = 0;
sign = 1;
}
}
return node;
}
主函数
int main() {
char* treeStr = "(1 (2 (4) (5)) (3 (6)))";
int index = 0;
struct TreeNode* root = buildTreeFromParenthesis(treeStr, &index);
// 其他操作...
return 0;
}
4.凹入表示法
凹入表示法使用缩进来表示树的结构:每个节点都在上一级节点的下方,并且比上一级节点缩进一定的距离。通过缩进的方式,可以清晰地展示树的层次结构和节点之间的嵌套关系。
结构体
#include <stdio.h>
#include <stdlib.h>
struct TreeNode {
int value;
struct TreeNode* firstChild;
struct TreeNode* nextSibling;
};
创建树
struct TreeNode* createTreeNode(int value) {
struct TreeNode* node = (struct TreeNode*)malloc(sizeof(struct TreeNode));
node->value = value;
node->firstChild = NULL;
node->nextSibling = NULL;
return node;
}
凹入表示法
struct TreeNode* buildTreeFromIndented(char* treeStr, int* index, int level) {
struct TreeNode* node = NULL;
while (treeStr[*index] != '\0') {
char c = treeStr[*index];
(*index)++;
if (c == '\n') {
continue;
}
if (c == ' ') {
continue;
}
if (c == '-') {
level++;
continue;
}
int value = c - '0';
if (node == NULL) {
node = createTreeNode(value);
} else {
struct TreeNode* child = createTreeNode(value);
if (node->firstChild == NULL) {
node->firstChild = child;
} else {
struct TreeNode* sibling = node->firstChild;
while (sibling->nextSibling != NULL) {
sibling = sibling->nextSibling;
}
sibling->nextSibling = child;
}
}
int nextChar = treeStr[*index];
if (nextChar == '\n') {
level--;
} else if (nextChar == '-') {
continue;
} else {
break;
}
}
return node;
}
主函数
int main() {
char* treeStr = "1\n-2\n--4\n--5\n-3\n--6\n";
int index = 0;
struct TreeNode* root = buildTreeFromIndented(treeStr, &index, 0);
// 其他操作...
return 0;
}