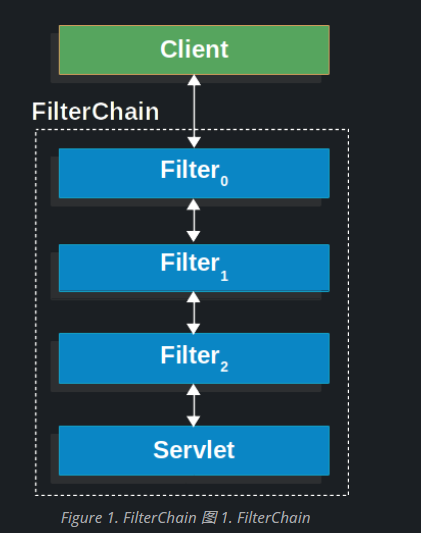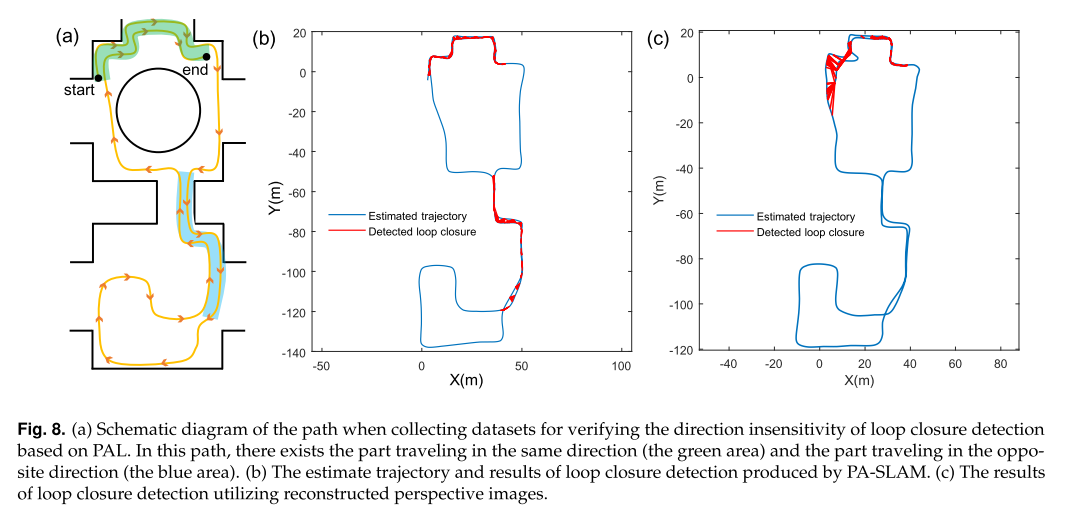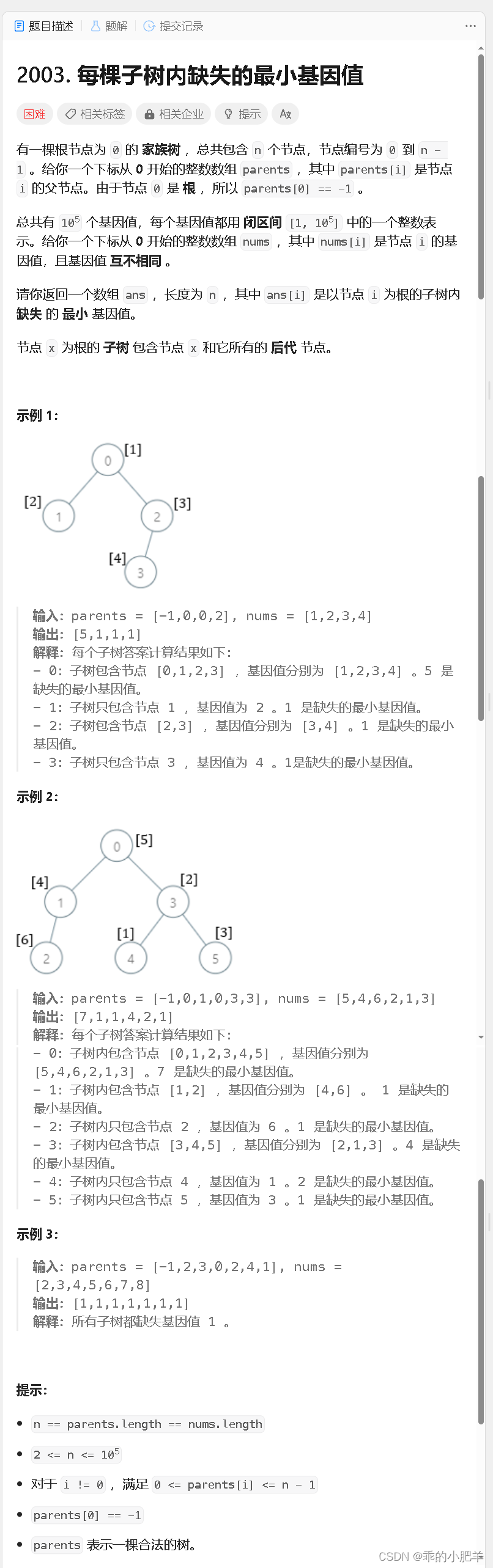
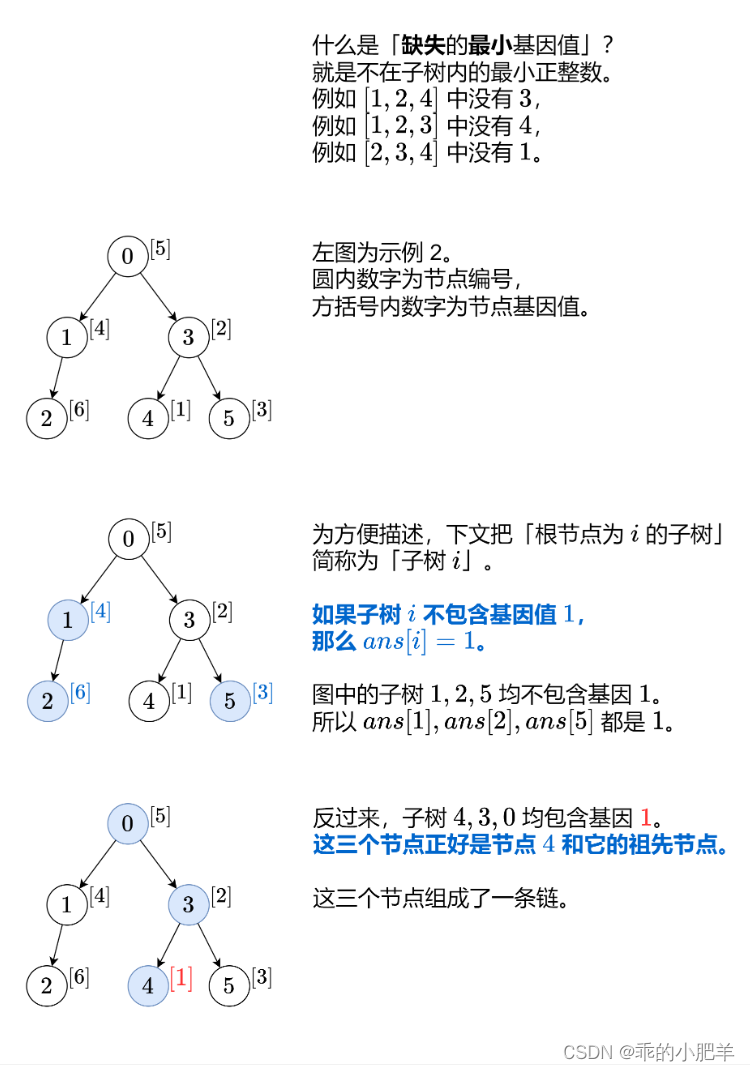
图片借用B站灵茶山文艾府


打卡代码(记得看,有注释):
class Solution {
public:
vector<int> smallestMissingValueSubtree(vector<int> &parents, vector<int> &nums) {
int n = parents.size();
vector<int> ans(n,1);
auto it = find(nums.begin(),nums.end(),1);//寻找基因值为1的编号,然后向上合并
if(it == nums.end()) return ans;//未找到基因值为1的编号就返回
unordered_set<int> vist;//存放基因值
stack<int> stk;
int node = it - nums.begin();//找到基因值为1的节点编号,第一次是基因值为1的编号,下次就是从下往上的顺序的节点编号了
//node编号定义为当前子树根节点的编号
//从基因值为1的节点编号开始可以保证以O(N)的复杂度遍历完并判断完成
//建树,建一个存子树节点的数组
//为什么这么建树呢,因为我们遍历当前子树的时候,一定要遍历完下面的子树才能
//去遍历上面的子树,这样才能确保我们从下往上时我们的基因值是正确的
//假设不这样遍历的话,那么就导致,再往上遍历的时候,最小基因值的判断就不包括下面的子树了
//而我们从基因值为1的节点编号的子树开始,在遍历子树的时候能确保我们在计算基因值的的时候,能包含上次最小的基因值
vector<vector<int>> g(n + 100);
for(int i = 1;i < n;i++) g[parents[i]].push_back(i);//建一棵下标为父节点的,内部元素为邻近子节点的编号,就是相当于该节点的
//直连的子节点
int min_val = 2;//最小基因值
int pre = -1;//pre定义为当前node根节点的树的一棵子树的编号,
while(node >= 0)
{
vist.insert(nums[node]);//插入到基因值序列中
//插入完之后进行遍历该节点的子树,确保我们是从下往上遍历的
for(auto son:g[node])
{
if(son != pre)//如果该子节点没有被遍历,加入到栈中
{
stk.push(son);
}
}
//遍历当前node根节点的子节点
while(!stk.empty())
{
int root = stk.top();
stk.pop();
vist.insert(nums[root]);
for(auto son:g[root]) stk.push(son);
}
while(vist.count(min_val)) min_val++;//如果没有当前最小基因值,那当前node子树的的最小基因值就是min_val
ans[node] = min_val;
pre = node;
node = parents[node];
}
return ans;
}
};