一、两种基本模型
1.加密模型

A要给B发信息,那就拿B的公钥加密,传给B,B收到后会拿他自己的私钥解密得到明文。
2.认证模型(数字签名)
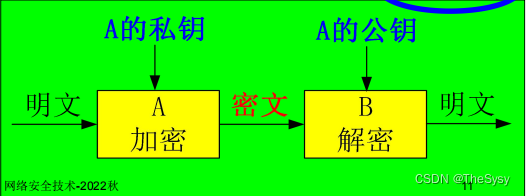
A用自己的私钥加密,传输之后,别人拿A的公钥解密,如果解密成功,那就可以说明这条信息是A发的。
二、公钥密码体制数学基础
1.单向函数
1)给定x,正着计算是容易的
2)给定y,逆着计算是不可行的
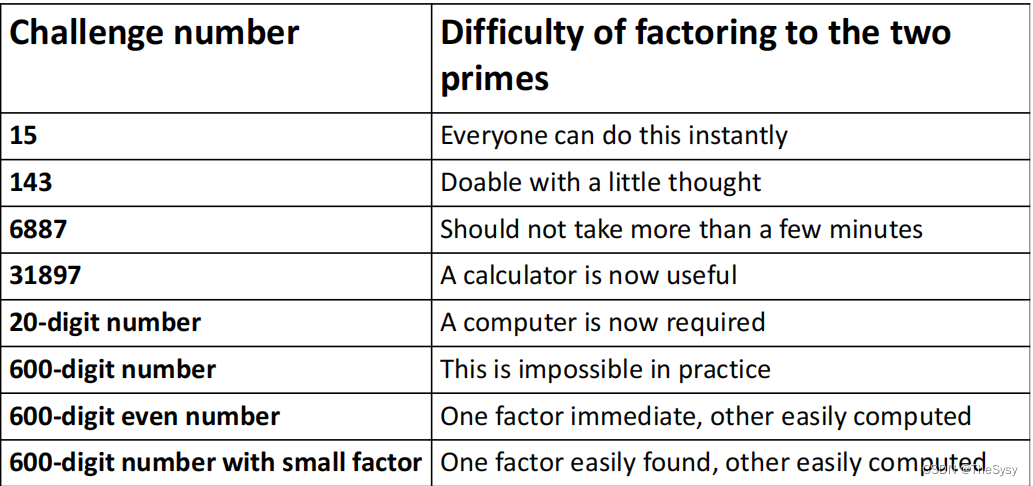
就比如说大整数分解,在数很大的时候,要遍历所有所有比它小的素数,这被认为是困难的。
三、Diffie-Hellman
这个和上面提到的标准的公钥模型有区别,这个算法简单来说,就是双方通过一个公共的信息(q,a),计算得到一个只有他们两人知道的共享密钥k。

1.首先a和b共享两个全局参数q和a,q是个素数,a是q的本原根。
本原根:a是q的本原根,那么a的1到q-1次方分别模q,分别得到不同的数。
2.然后a和b分别各自选一个数,
,都小于q,作为各自的私钥。
3.他们分别用,
算各自的公钥,公钥=a的密次幂模q
,
,并发送给对方,这个计算就相当于单向函数中的正着算,被认为是容易的。
4.a和b收到对方的发来的公钥后,计算共享密钥,共享密钥=公共的密次幂模q
对于a来说,
对于b来说,
这两个算出来的k是相等的,双方就有了共享密钥,这个密钥可以用来例如作为AES的密钥。
四、中间人攻击Man in the Middle attack
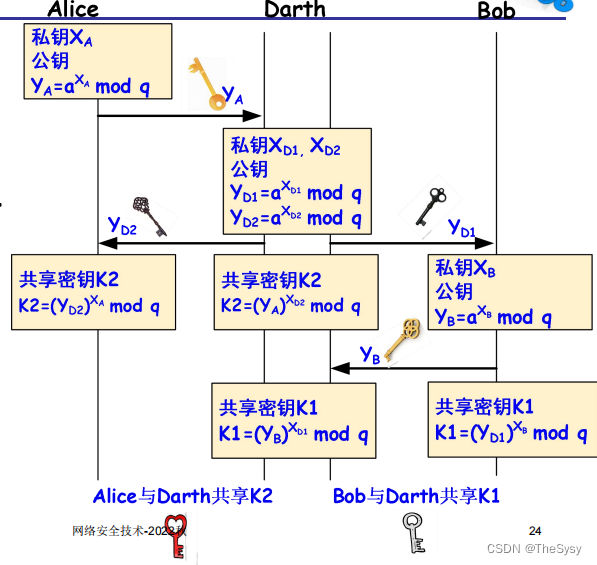
先看左半边,a选定私钥之后,计算自己的公钥发给b,这个信息被大司截获,大司选定一个私钥,用这个私钥计算公钥,还给a。a用大司给他的公钥计算出k2来,之后就用k2来加密例如AES了。
然后右半边,b选定私钥之后,计算自己的公钥发给a,大司也把他截获了,自己选定另一个私钥,计算公钥还给b。b拿大司给他的公钥算出来k1,之后就用k1来加密了。
这样,大司要计算k1=b的公钥的密次幂,k2=a的公钥的密次幂,所以它是有k1和k2的,之后a和b所有的数据通信对大司来说都是透明的了。
这个问题的根本在于,a和b分别不能知道收到的公钥是否是对方发来的,如果a能验证收到的公钥是b发来的,b反之也可以,那么就不会被大司截胡了,因为大司发来的一验证就直接露馅了。
五、RSA算法
这个算法是生成自己的私钥和公钥的算法,就像一开始提到的标准的公钥密码体制,生成自己的私钥和公钥后,别人要给自己发消息,就拿自己的公钥加密,自己收到后拿自己的私钥解密。

1.密钥产生流程
1)选p,q两个不相等的素数。
2)算n=p*q。
3)算phi(n)=(p-1)*(q-1)。
4)选一个和phi(n)互质的数e,1<e<phi(n)
5)拿phi(n)和e算d,de和1模phi(n)同余,简单来说就是d*e模phi(n)=1。这样能算出很多个d,取最小的那个。
6)这样就有了公钥PK={e, n}, 私钥SK={d, n}
别人有了公钥,e和n是算不出来d的,因为d是拿e和phi(n)算的,要求phi(n)就得分解n,这被认为是不可能的。
2.加密:
1)将明文转换为一个数M,M<n
2)密文
3.解密:
明文
4.与对称加密结合
RSA加密速度比DES慢1000倍,那么加密大量明文就不适用。
考虑用RSA加密密钥,再用对称加密例如AES加密。
考虑以下场景,a要和b通信,那么a就通过RSA生成自己的公私钥,b生成AES加密用的密钥。b将密钥用a的公钥加密,发送给a,a用自己的私钥解密,拿到密钥。
之后双方通信就有共享密钥了。