在2023年4月29日的力扣103夜喵双周赛上，我被第四题所困扰，又于2023年5月4日早上的Linux系统基础课上，我初次接触到了树状数组。从那时候我就想写一篇博客记录一下，鸽到了现在…
参考视频

树状数组的作用

• 维护一个序列
• 修改某一个数，并且快速求得前缀和 $O(logn)$

前置知识

lowbit() 运算：非负整数x在二进制表示下最低位1及其后面的0构成的数值。
示例：
$lowbit(2)=lowbit({[10]}_2)=2$
$lowbit(12)=lowbit({[1100]}_2)=lowbit({[100]}_2)=4$

代码

int lowbit(int x)
{
    return x & -x;
}

基本思想

使用树结构维护”前缀和”
我们令原数组为a[i] ,树状数组为t[i]

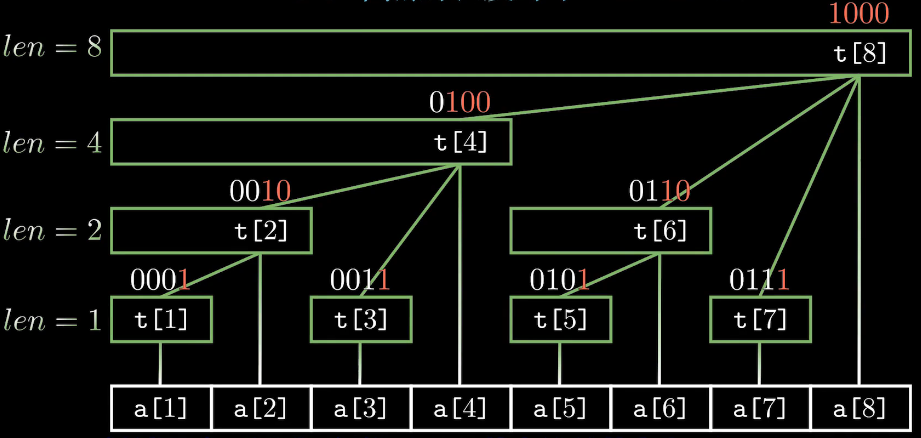
• 每个结点$t[x]$保存以$x$为根的子树中叶结点值的和
• 每个结点覆盖的长度为$lowbit(x)$， 如t[2]长度为2，t[12]长度为4
• t[x]结点的父结点为$t[x+lowbit(x)]$
• 树的深度为$log2n+1$

两个操作

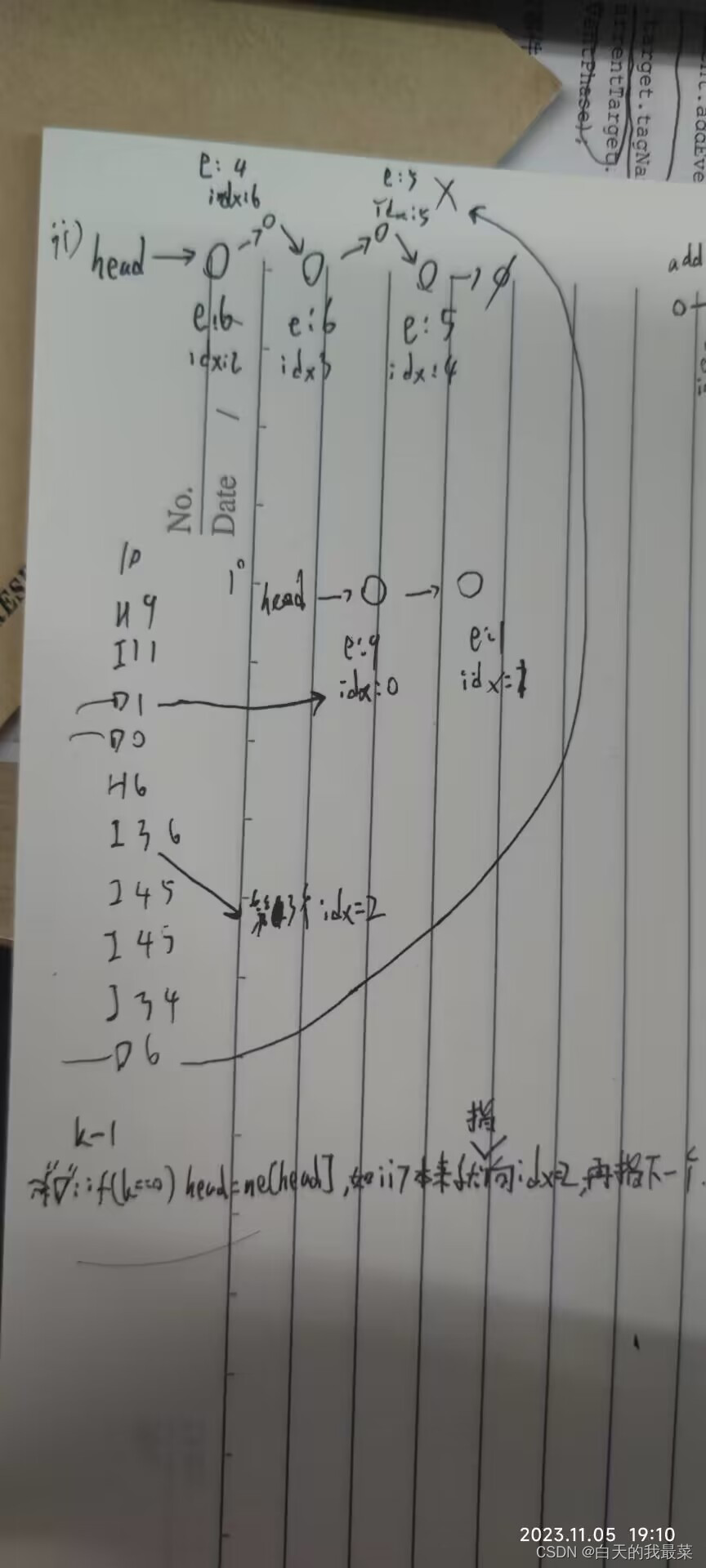
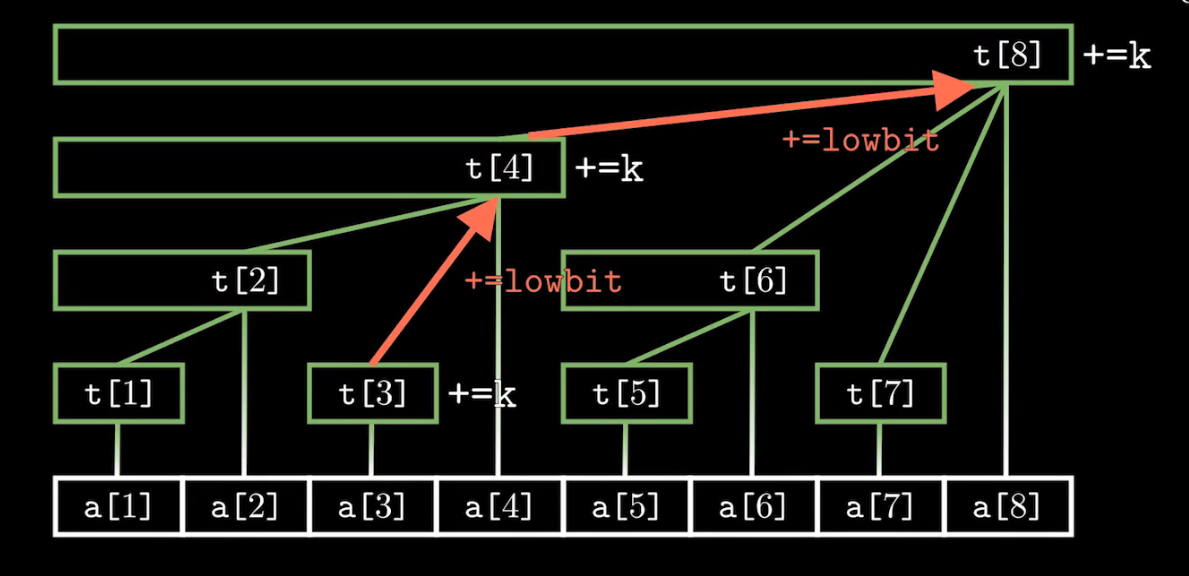
1. void add(int x, int c)：a[x]的值加c

以add(3,k)为例，如图所示

代码

void add(int x, int c)
{
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}

也可以这样

void update(int x, int c) {
	while (x <= n){
		tree[x] += c;
        x += lowbit(x);
	}
}

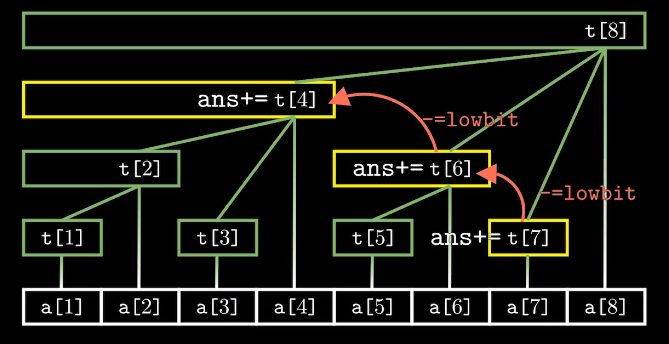
2. query(int x) ：查询前x个数的和

LL query(int x)
{
    LL res = 0;
    for (int i = x; i; i -= lowbit(i))
        res = max(res, tr[i]);
    return res;
}

or

ll getsum(int x) {
    ll ans = 0;
    while (x > 0) {
        ans += tree[x];
        x -= lowbit(x);
    }
    return ans;
}

代码

#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int n, m;
int tr[N];

int lowbit(int x) {
    return x & -x;
}

void add(int x, int v) {
    for (int i = x; i <= n; i += lowbit(i))
        tr[i] += v;
}

int query(int x) {
    int res = 0;
    for (int i = x; i; i -= lowbit(i))
        res += tr[i];
    return res;
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) {
        int v;
        cin >> v;
        add(i, v);
    }
    while (m --) {
        int x, a, b;
        cin >> x >> a >> b;
        if (x == 1)
            add(a, b);
        else
            cout << query(b) - query(a - 1) << endl;
    }

    return 0;
}