题目链接：Educational Codeforces Round 2 D




 

题目 

给你两个圆。求它们相交处的面积。

输入

第一行包含三个整数 x1, y1, r1 (  - 109 ≤ x1, y1 ≤ 109, 1 ≤ r1 ≤ 109 ) - 第一个圆的圆心位置和半径。

第二行包含三个整数 x2, y2, r2 (  - 109 ≤ x2, y2 ≤ 109, 1 ≤ r2 ≤ 109 ) - 圆心位置和第二个圆的半径。

输出

打印圆的交点面积。如果绝对误差或相对误差不超过 10 - 6 ，答案将被视为正确。

 

题解

如果两个圆不相交，答案是0。我们可以只用整数计算来检查这种情况(只需比较中心之间距离的平方与半径和的平方)。如果其中一个圆完全在另一个圆里，那么答案就是小圆的平方。我们也可以只用整数计算来检查这种情况(只需比较中心之间距离的平方与半径差的平方)。

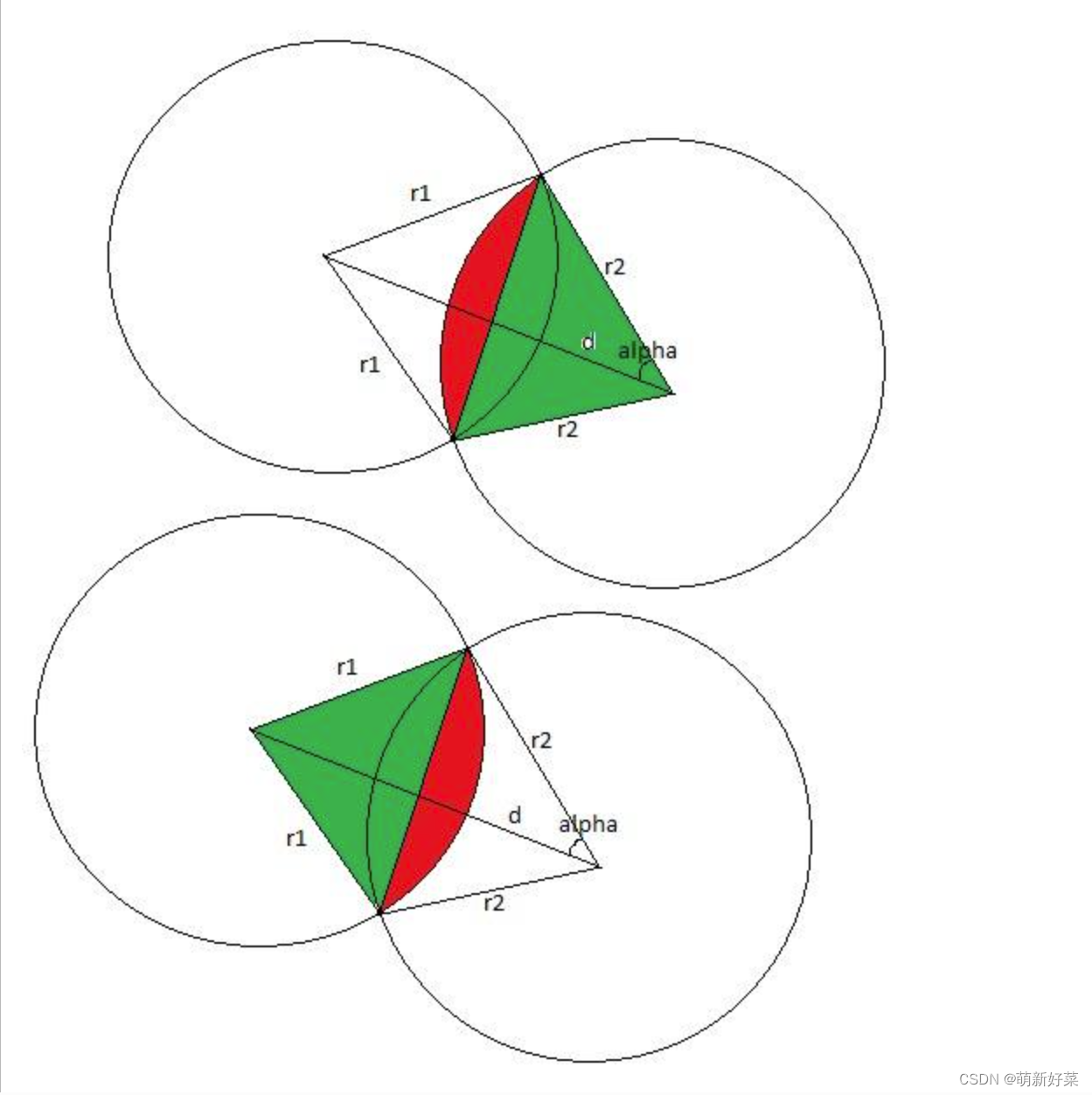
现在我们考虑一般情况。答案等于两个圆段的和。让我们考虑一个三角形的顶点在圆的中心和圆的交点上。在这个三角形中，我们知道所有的三条边，所以我们可以计算圆段的角度。我们可以计算扇形的平方。现在我们唯一要做的就是减去三角形的正方形顶点在圆心和圆的交点处。我们可以通过计算外积绝对值的一半来求。所以我们有以下公式:

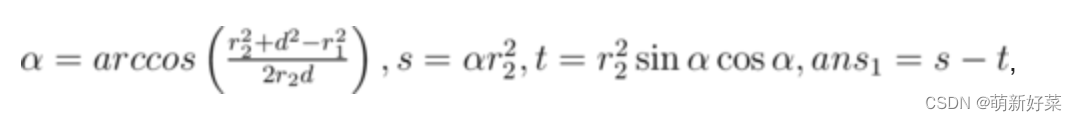
d是圆心之间的距离。我们也应该对第二圈做同样的事情通过替换指标1≤√2。

 

代码

 

// Problem: D. Area of Two Circles' Intersection
// Contest: Codeforces - Educational Codeforces Round 2
// URL: https://codeforces.com/contest/600/problem/D
// Memory Limit: 256 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef long double ld;

const int N = 2e5+5;

ld cal(ld r1,ld r2,ld d){
	ld t=2*acos((r1*r1+d*d-r2*r2)/2/r1/d);
	ld s1=r1*r1/2*t;
	ld s2=r1*r1/2*sin(t);
	return s1-s2;
}

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	
	ld pi=acos(-1);
	ld x1,x2,y1,y2,r1,r2,d,ans;
	cin>>x1>>y1>>r1>>x2>>y2>>r2;
	d=sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
	if(d>=r1+r2){
		ans=0;
	}
	else if(d<=fabs(r1-r2)){
		ans=min(r1,r2)*min(r1,r2)*pi;
	}
	else{
		ans=cal(r1,r2,d)+cal(r2,r1,d);
	}
	//printf("%.20llf\n",ans);
	cout<<fixed<<setprecision(20)<<ans<<"\n";
	
	
	return 0;	

}