一、策略的改进
假设新的贪婪策略π0与旧的策略π效果相当,但并不优于π。由此得出vπ=vπ0,且根据之前的推导可以得出:对于所有的s∈S
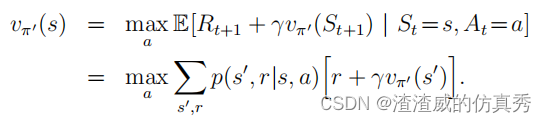
这与贝尔曼最优方程相同,因此,vπ0是v∗,π和π0是最佳策略。因此,策略改进给我们一个更好的策略,除非原始策略已经是最佳的。迄今为止考虑的是确定性策略的特殊情况。在一般情况下,随机策略π规定了每个状态s下采取每个行动a的概率,即π(a|s)。这些思想都很容易扩展到随机策略。特别是,策略改进定理可以按照定义适用于随机情况。
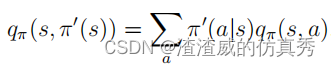
如果在策略改进步骤中存在并列的情况,即存在多个行动能够达到最大值,那么在随机情况下,我们并不需要从它们中选择一个单一的行动。相反,每个最大化的行动可以在新的贪婪策略中被分配一部分被选择的可能性。只要所有次优的行动都被赋予零概率,任何分配方案都是允许的。
二、典型示例
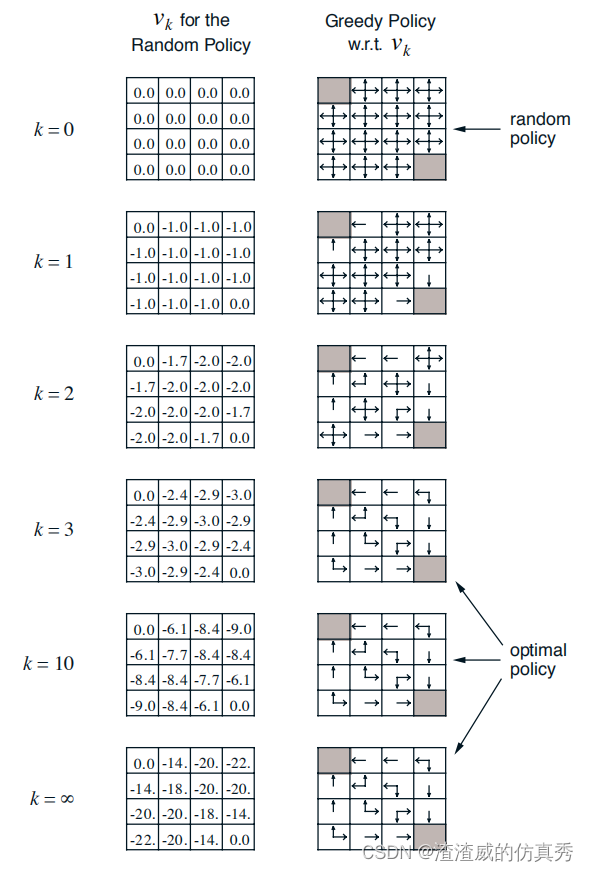
图1
图1是小型网格世界中迭代策略评估的收敛过程的例子。左列是随机策略(所有行动均等)的状态值函数的近似序列。右列是与值函数估计相对应的贪婪策略的序列(箭头表示所有实现最大值的行动)。最后一项政策只保证比随机政策有所改进,但在这种情况下,以及在第三次迭代后的所有政策中,它们都是最优的。上图最后一行展示了随机策略的策略改进示例。在这里,原始策略π是等概率的随机策略,而新策略π0是相对于vπ的贪婪策略。底部左边的图显示了vπ的值函数,底部右边的图显示了可能的π0集合。π0图中箭头较多的状态是那些在多个行动达到最大值的状态;这些行动之间的任何概率分配都是允许的。通过观察任何此类政策的值函数vπ0(s),可以看出在所有状态s∈S下,vπ0(s)可以是∇1、⍶2或∇3,而vπ(s)最多为-14。因此,对于所有s∈S,vπ0(s)≥vπ(s),这说明了策略改进。尽管在这种情况下新政策π0碰巧是最优的,但通常情况下只能保证有所改进。