1. 题目链接:129. 求根节点到叶节点数字之和
2. 题目描述:
给你一个二叉树的根节点
root,树中每个节点都存放有一个0到9之间的数字。每条从根节点到叶节点的路径都代表一个数字:
- 例如,从根节点到叶节点的路径
1 -> 2 -> 3表示数字123。计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
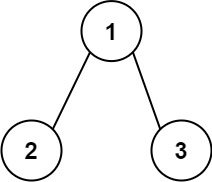
示例 1:
输入:root = [1,2,3] 输出:25 解释: 从根到叶子节点路径 1->2 代表数字 12 从根到叶子节点路径 1->3 代表数字 13 因此,数字总和 = 12 + 13 = 25示例 2:
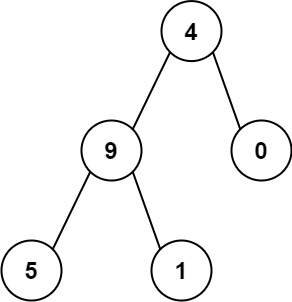
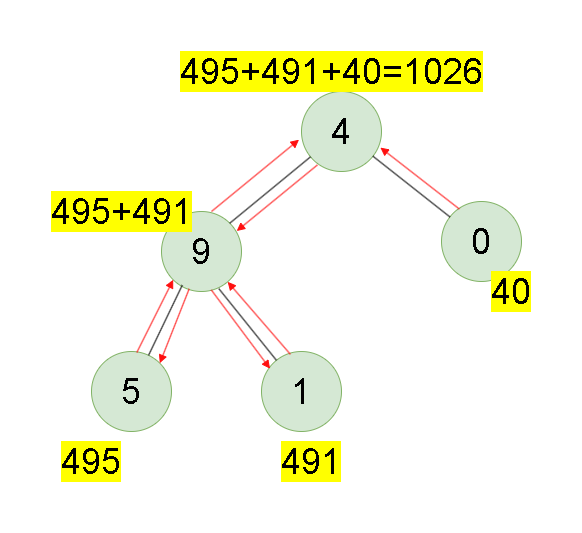
输入:root = [4,9,0,5,1] 输出:1026 解释: 从根到叶子节点路径 4->9->5 代表数字 495 从根到叶子节点路径 4->9->1 代表数字 491 从根到叶子节点路径 4->0 代表数字 40 因此,数字总和 = 495 + 491 + 40 = 1026提示:
- 树中节点的数目在范围
[1, 1000]内0 <= Node.val <= 9- 树的深度不超过
10
3. 解法(前序遍历)
前序遍历的顺序为根结点->左子树->右子树
3.1 算法思路:
在前序遍历的过程中,我们可以往左右子树传递信息,并且在回溯时得到左右子树的返回值。递归函数可以帮助我们完成两件事情:
- 将父节点的数字与当前节点的信息整合到一起,计算出当前节点的数字,然后传递到下一层进行递归
- 当遇到叶子节点的时候,就不再向下传递信息,而是将整合的结果向上一种回溯到根节点
在递归结束时,根节点需要返回的值也就被更新为了整棵树的数字之和
3.2 算法流程:
递归函数设计:int dfs(TreeNode* root,int num)
- 返回值:当前子树计算的结果(数字和)
- 参数num:递归过程中往下传递的信息(父节点的数字)
- 函数作用:整合父节点的信息与当前节点的信息计算当前节点数字,并向下传递,在回溯时返回当前子树(当前节点作为子树根节点)数字和。
递归函数流程:
- 当遇到空节点的时候,说明这条路从根节点开始没有分支,返回
0 - 结合父节点传下的信息以及当前节点的
val,计算出当前节点数字num - 如果当前节点是叶子节点,直接返回整合后的结果
num - 如果当前节点不是叶子节点,将
num传到左右子树中去,得到左右子树节点路径的数字和,然后相加后返回结果
3.3 C++算法代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int sumNumbers(TreeNode* root) {
return dfs(root,0);
}
int dfs(TreeNode*root,int num)
{
num=num*10+root->val;
//如果左右子树为空,说明是没有左右子树,返回num
if(root->left==nullptr&&root->right==nullptr)
return num;
int ret=0;
if(root->left)
ret+=dfs(root->left,num);
if(root->right)
ret+=dfs(root->right,num);
return ret;
}
};