503.下一个更大元素II
题目链接:https://leetcode.com/problems/next-greater-element-ii/
解法:
由于是循环数组,可以直接把两个数组拼接在一起,然后使用单调栈求下一个最大值。
写法上,可以巧妙一些,循环的长度为2*len(nums),通过 i%len(nums)来实现两次遍历数组。
边界条件:无
时间复杂度:O(n)
空间复杂度:O(n)
class Solution(object):
def nextGreaterElements(self, nums):
dp = [-1] * len(nums)
stack = []
for i in range(len(nums)*2):
while stack and nums[i%len(nums)] > nums[stack[-1]]:
dp[stack[-1]] = nums[i%len(nums)]
stack.pop()
stack.append(i%len(nums))
return dp 42. 接雨水
题目链接:https://leetcode.com/problems/trapping-rain-water/
解法:
按照列来计算的话,宽度一定是1了,我们再把每一列的雨水的高度求出来就可以了。
每一列雨水的高度,取决于,该列 左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度。
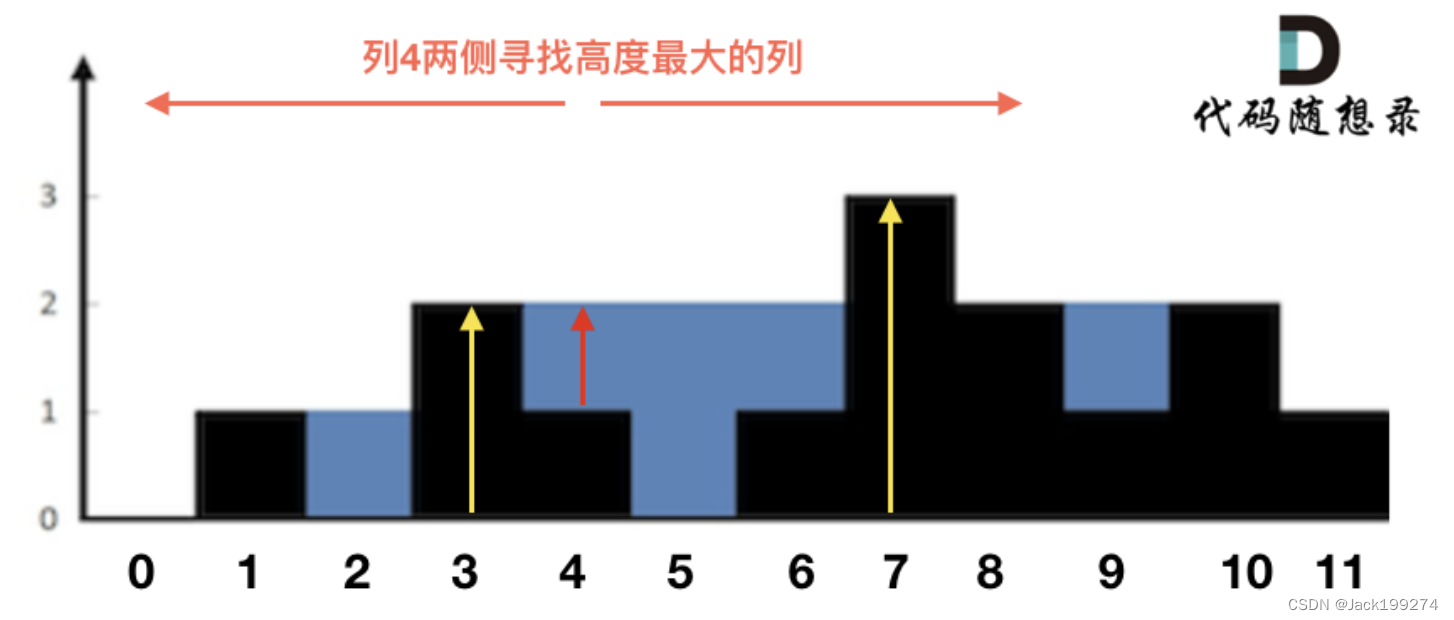
使用双指针来计算。
为了得到两边的最高高度,使用了双指针来遍历,每到一个柱子都向两边遍历一遍,这其实是有重复计算的。我们把每一个位置的左边最高高度记录在一个数组上(maxLeft),右边最高高度记录在一个数组上(maxRight),这样就避免了重复计算。
单调栈的做法,代码随想录的解法写得巨复杂,直接不想看了。其实没那么复杂,但是还是很巧妙,主要出来的柱子的顺序不是从左到右的。
这个和每日温度的题目思路很像,只要找到右边第一个更大的元素,就可以把栈头pop,计算雨水面积,因为是从栈头到栈尾递增,那么左边的元素大于等于栈头,就可以储水了。
雨水高度是 min(凹槽左侧高度, 凹槽右侧高度) - 凹槽底部高度。
雨水宽度是 凹槽右侧的下标 - 凹槽左侧的下标 - 1。
题解看leetcode中文区的比较好懂:

边界条件:无
时间复杂度:O(n)
空间复杂度:O(n)
# 单调栈
class Solution(object):
def trap(self, height):
stack = [0]
result = 0
for i in range(1, len(height)):
while stack and height[i] > height[stack[-1]]:
idx = stack.pop()
if stack:
# 如果 stack[-1] 和 idx 对应的值相同,那就面试为0
h = min(height[stack[-1]], height[i]) - height[idx]
w = i - stack[-1] - 1
result += h * w
stack.append(i)
return result# 双指针
class Solution(object):
def trap(self, height):
max_left, max_right = [0] * len(height), [0] * len(height)
max_left[0] = height[0]
max_right[-1] = height[-1]
# 求i左边的最大值
for i in range(1, len(height)):
max_left[i] = max(height[i], max_left[i-1])
# 求i右边的最大值
for i in range(len(height)-2, -1, -1):
max_right[i] = max(height[i], max_right[i+1])
result = 0
for i in range(len(height)):
# 取决于左遍最大值和右边最大值之间的较小值
count = min(max_left[i], max_right[i]) - height[i]
if count > 0:
result += count
return result84. 柱状图中的最大矩形
题目链接:
解法:
这道题,代码随想录连怎能计算矩形的面积都没写,就直接给了代码,默认大家懂了...
这题看leetcode的中文区解法比较好。
计算矩形的最大面积,可以枚举以每个柱形为高度的最大矩形的面积。
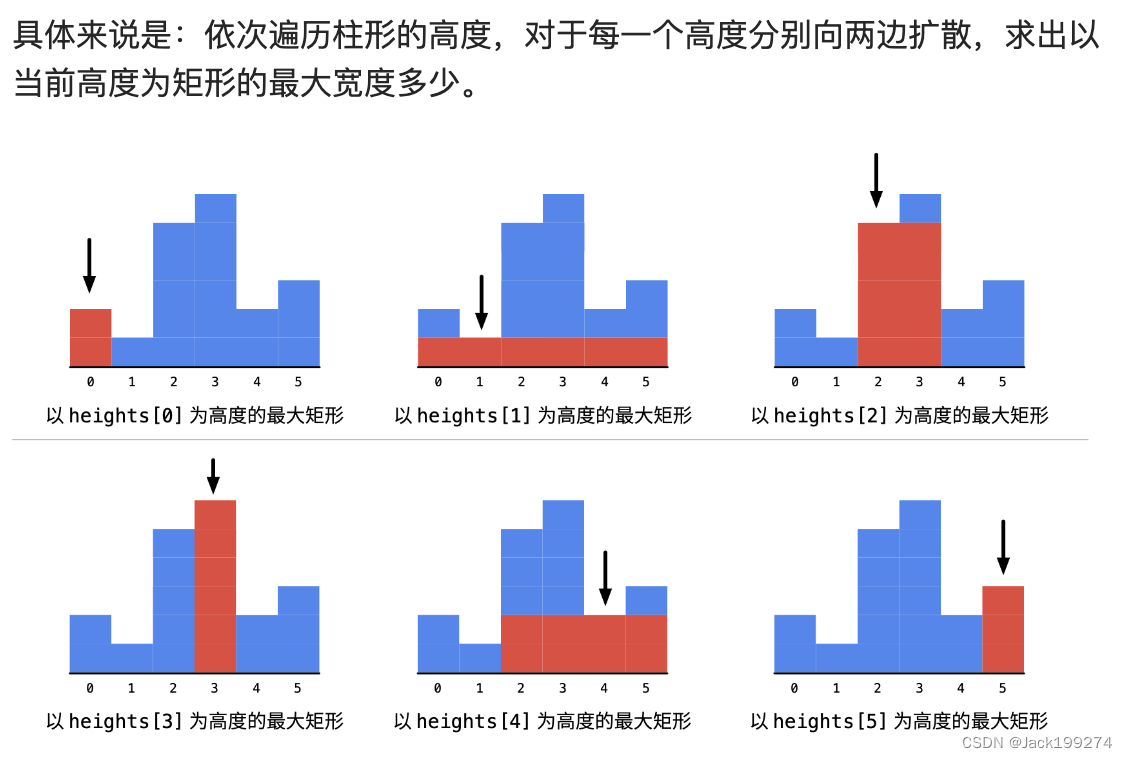
为此,我们需要:
左边看一下,看最多能向左延伸多长,找到大于等于当前柱形高度的最左边元素的下标;
右边看一下,看最多能向右延伸多长;找到大于等于当前柱形高度的最右边元素的下标。
对于每一个位置,我们都这样操作,得到一个矩形面积,求出它们的最大值。
所以,双指针的写法,可以记录每个元素的左边第一个更小元素的下标和右边第一个更小元素的下标,那么面积等于 (right_min - left_min - 1) * height[i].
相比之下,单调栈的写法简洁多了。这里用的单调减栈,也就是栈头到栈尾是递减的(列表表现为从左到右递增)。
42. 接雨水 (opens new window)是找每个柱子左右两边第一个大于该柱子高度的柱子,而本题是找每个柱子左右两边第一个小于该柱子的柱子。不同的是,接雨水第一个柱子和最后一个柱子没法储水,但这里第一个柱子和最后一个都要计算以他们为高度的面积,所以heights的前后要插入0。
边界条件:无
时间复杂度:双指针O(n)
空间复杂度:双指针O(n)
# 双指针
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
size = len(heights)
# 两个DP数列储存的均是下标index
min_left_index = [0] * size
min_right_index = [0] * size
result = 0
# 记录每个柱子的左侧第一个矮一级的柱子的下标
min_left_index[0] = -1 # 初始化防止while死循环
for i in range(1, size):
# 以当前柱子为主心骨,向左迭代寻找次级柱子
temp = i - 1
while temp >= 0 and heights[temp] >= heights[i]:
# 当左侧的柱子持续较高时,尝试这个高柱子自己的次级柱子(DP
temp = min_left_index[temp]
# 当找到左侧矮一级的目标柱子时
min_left_index[i] = temp
# 记录每个柱子的右侧第一个矮一级的柱子的下标
min_right_index[size-1] = size # 初始化防止while死循环
for i in range(size-2, -1, -1):
# 以当前柱子为主心骨,向右迭代寻找次级柱子
temp = i + 1
while temp < size and heights[temp] >= heights[i]:
# 当右侧的柱子持续较高时,尝试这个高柱子自己的次级柱子(DP
temp = min_right_index[temp]
# 当找到右侧矮一级的目标柱子时
min_right_index[i] = temp
for i in range(size):
area = heights[i] * (min_right_index[i] - min_left_index[i] - 1)
result = max(area, result)
return resultclass Solution(object):
def largestRectangleArea(self, heights):
heights.insert(0, 0)
heights.append(0)
stack = [0]
result = 0
for i in range(1, len(heights)):
# 维持的单调减栈,左边元素肯定更小,右边遇到更小的就计算面积
while stack and heights[i] < heights[stack[-1]]:
mid_idx = stack.pop()
if stack:
h = heights[mid_idx]
w = i - stack[-1] - 1
result = max(result, h * w)
stack.append(i)
return result