leetCode 322.零钱兑换完全背包 + 动态规划 + 记忆化搜索 + 递推 + 空间优化 + 画递归树

news2024/12/24 8:52:45

关于此题我的往期文章：LeetCode 322.零钱兑换完全背包 + 动态规划_呵呵哒(￣▽￣)"的博客-CSDN博客https://heheda.blog.csdn.net/article/details/133386579看本期文章时，可以先回顾一下动态规划入门知识和完全背包理论和实战：

0-1背包完全背包 + 至多/恰好/至少 + 空间优化 + 常见变形题（实战力扣题）-CSDN博客https://blog.csdn.net/weixin_41987016/article/details/134210521?spm=1001.2014.3001.5501leetCode 198.打家劫舍动态规划入门:从记忆化搜索到递推-CSDN博客https://blog.csdn.net/weixin_41987016/article/details/134179583?spm=1001.2014.3001.5501给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。你可以认为每种硬币的数量是无限的。

最优的子结构性质，这是解决动态规划问题的关键。最优解可以从其子问题的最优解构造出来。如何将问题分解成子问题？

（1）递归

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        int n = coins.size();
        function<int(int,int)> dfs=[&](int i,int c) -> int {
            if(i < 0) {
                if(c == 0) return 0;
                else return INT_MAX/2;// 除 2 是防止下面 + 1 溢出
            }
            if(c < coins[i]) return dfs(i-1,c);
            return min(dfs(i-1,c),dfs(i,c-coins[i])+1);     
        };
        int ans = dfs(n-1,amount);
        return ans<INT_MAX/2?ans:-1;
    }
};

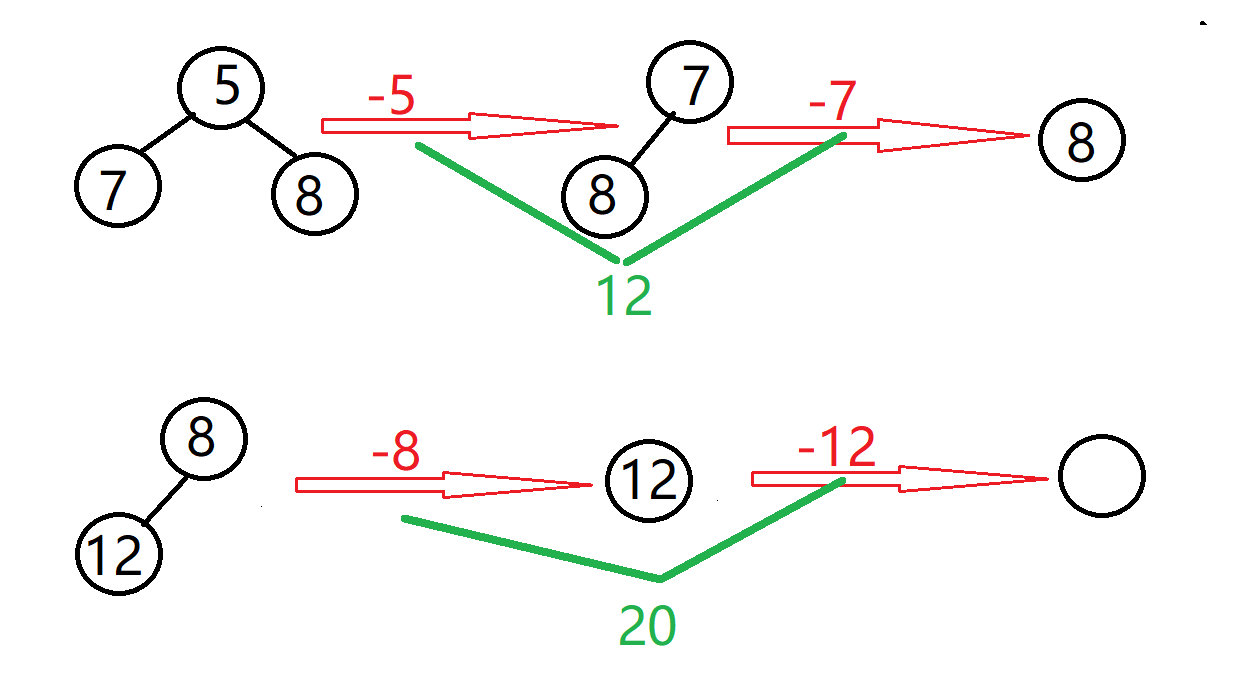
在上面的递归树中，可以看到有许多子问题被多次计算。例如，F(1)被计算了13次。为了避免重复的计算，可以将每个子问题的答案存在一个数组中进行记忆化，如果下次还要计算这个问题的值直接从数组中取出返回即可，这样能保证每个子问题最多只被计算一次。我们接着往下看~

（2）递归搜索 + 保存计算结果 = 记忆化搜索

class Solution {
public:
    // 记忆化搜索
    int coinChange(vector<int>& coins, int amount) {
        int n = coins.size(),memo[n+1][amount+1];
        memset(memo,-1,sizeof(memo));
        function<int(int,int)> dfs=[&](int i,int c) -> int {
            if(i < 0) {
                if(c == 0) return 0;
                else return INT_MAX/2;// 除 2 是防止下面 + 1 溢出
            }
            int& res = memo[i][c];
            if(res != -1) return res;
            if(c < coins[i]) return res=dfs(i-1,c);
            return res=min(dfs(i-1,c),dfs(i,c-coins[i])+1);     
        };
        int ans = dfs(n-1,amount);
        return ans<INT_MAX/2?ans:-1;
    }
};

时间复杂度：O(n * amount)
空间复杂度：O(n * amount)

（3）1:1 翻译成递推

class Solution {
public:
    // 1:1 翻译成递推
    int coinChange(vector<int>& coins, int amount) {
        int n = coins.size(),f[n+1][amount+1];
        memset(f,0x3f,sizeof(f));
        f[0][0]=0;
        for(int i=0;i<n;i++) {
            for(int c=0;c<=amount;c++) {
                if(c<coins[i]) f[i+1][c] = f[i][c];
                else f[i+1][c] = min(f[i][c],f[i+1][c-coins[i]]+1); 
            }
        }
        int ans = f[n][amount];
        return ans<0x3f3f3f3f?ans:-1;
    }
};

时间复杂度：O(n * amount)
空间复杂度：O(n * amount)

（4）空间优化：两个数组（滚动数组）

class Solution {
public:
    // 空间优化：两个数组（滚动数组）
    int coinChange(vector<int>& coins, int amount) {
        int n = coins.size(),f[2][amount+1];
        memset(f,0x3f,sizeof(f));
        f[0][0]=0;
        for(int i=0;i<n;i++) {
            for(int c=0;c<=amount;c++) {
                if(c<coins[i]) f[(i+1)%2][c] = f[i%2][c];
                else f[(i+1)%2][c] = min(f[i%2][c],f[(i+1)%2][c-coins[i]]+1); 
            }
        }
        int ans = f[n%2][amount];
        return ans<0x3f3f3f3f?ans:-1;
    }
};

时间复杂度：O(n * amount)
空间复杂度：O(amount)

（5）空间优化：一个数组

class Solution {
public:
    // 空间优化：两个数组（滚动数组）
    int coinChange(vector<int>& coins, int amount) {
        int n = coins.size(),f[amount+1];
        memset(f,0x3f,sizeof(f));
        f[0]=0;
        for(int i=0;i<n;i++) {
            for(int c=coins[i];c<=amount;c++) {
                f[c] = min(f[c],f[c-coins[i]]+1); 
            }
        }
        int ans = f[amount];
        return ans<0x3f3f3f3f?ans:-1;
    }
};