隐私保护多领域推荐的紧密度共聚类联邦概率偏好分布模型

论文链接

Federated Probabilistic Preference Distribution Modelling with Compactness Co-Clustering for Privacy-Preserving Multi-Domain Recommendation

引言

这篇论文提出的概率偏好分布是通过使用高斯分布来表示用户和项目的偏好。在论文中，作者提出了一种名为Federated Probabilistic Preference Distribution Modelling（联邦概率偏好分布建模）的新方法，该方法旨在解决隐私保护的多领域推荐问题。该方法在局部领域中建模用户/项目的概率偏好分布，并通过全局服务器聚合这些用户偏好分布。此外，作者还提出了一种紧凑性共聚类方法，用于在FPPDM++中利用用户的相似性关系。这种方法可以聚集具有相似口味或特征的用户。

方法论

这部分主要内容描述了Federated Probabilistic Preference Distribution Modelling（FPPDM）框架的设计以及如何解决Privacy-Preserving Multi-Domain Recommendation（PP-MDR）问题。FPPDM框架包括两个主要组件：1）本地领域建模组件，用于基于用户-项目评分交互来建模用户/项目的概率偏好分布；2）全局服务器聚合组件，负责聚合用户的偏好分布并将它们发送回到本地领域。
在FPPDM++中，作者提出了一种紧凑性共聚类方法，通过聚类用户的偏好分布来进一步提高推荐结果的准确性。这种方法可以聚集具有类似偏好或特征的用户，从而在保护用户隐私的同时提供更满意的推荐结果。
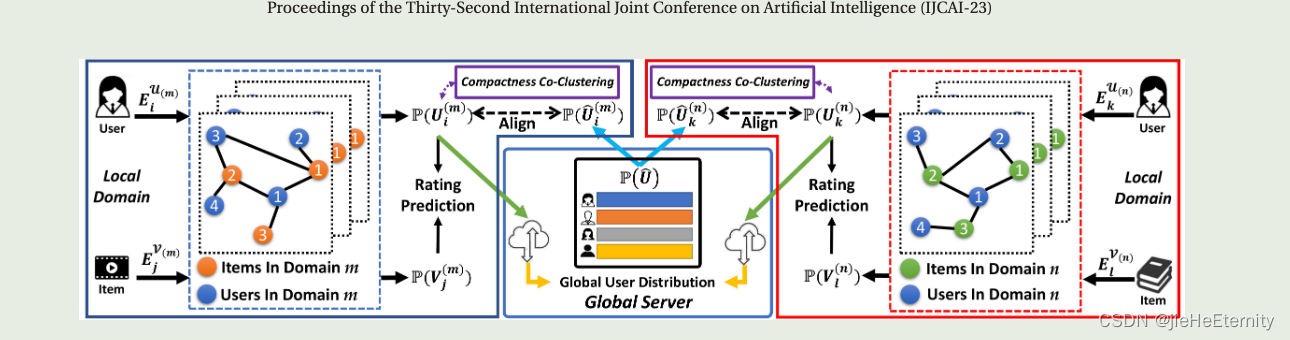
在这里插入图片描述

联邦概率偏好分布(FPPDM)

客户端领域建模组件

FPPDM涉及两个主要的组件：本地领域建模组件和全局服务器聚合组件。本地领域建模组件用于基于用户-项目评分交互来建模用户/项目的概率偏好分布。

定义用户和项目的一热编码向量；
利用图卷积神经网络（GCNN）建模用户/项目的偏好分布；
利用用户和项目交互的信息建立用户-项目交互图；
通过引入用户嵌入和项目嵌入来更好地聚合有用信息；
利用分布基于的度量学习损失函数训练模型来预测用户对项目的评分；
提出一个正则化项以减小相应的本地用户分布与全局用户分布之间的距离；
将训练好的本地用户分布发送到全局服务器。

为减小相应的本地用户分布与全局用户分布之间的距离，我们提出了以下正则化项：
$L_P = ∑_k (µ_k - µ)^2 + ∑_k (σ_k^2 - σ^2)^2$
其中， $D_k = diag(A_k 1)$ 表示 $k - t h$ 领域的度矩阵， $A_k$ 表示 $k - t h$ 领域的用户和项目的交互关系矩阵，I 是单位矩阵。
这个正则化项通过计算 $µ_k$ （k-th 领域的用户均值）与全局用户均值µ之间的平方差和 $σ_k^2$
（k-th 领域的用户协方差）与全局用户协方差 $σ^2$ 之间的平方差，来约束本地用户分布与全局用户分布的差异。通过优化这个正则化项，我们可以使本地用户分布与全局用户分布更接近，从而提高推荐效果。
使得本地用户和全局用户分布更加接近的作用如下：

改善用户偏好建模：本地用户分布与全局用户分布更接近可以更准确地建模用户偏好，特别是在数据稀疏性问题下。这有助于提高推荐系统的准确性和性能。
知识聚合和共享：通过使本地用户分布与全局用户分布更接近，可以更好地聚合和共享不同领域的用户信息，从而提高跨领域推荐的性能。
私保推荐：在保护用户隐私的前提下，使本地用户分布与全局用户分布更接近有助于实现高质量的跨领域推荐，同时避免了直接在不同领域上共享用户-项目评分信息的问题。
用户归类：通过使本地用户分布与全局用户分布更接近，可以更好地归类用户，从而在推荐过程中提供更个性化和准确的推荐结果。

全局服务器聚合组件

这部分的内容关于全局服务器聚合组件，主要讨论了在多个不同的领域之间聚合和更新用户分布。全局服务器聚合组件的主要任务是处理来自多个不同领域的用户分布，并将它们聚合到一个全局用户分布中，以便在多个领域之间共享知识。通过这种聚合和更新，全局服务器聚合组件可以在数据稀疏性问题下提高用户-项目建模的准确性。
全局服务器聚合组件的关键工作是：
聚合和更新全局用户分布：全局服务器聚合组件利用用户-项目评分交互来建模用户的偏好分布。在训练过程中，本地领域会将用户分布发送到全局服务器，并在全局服务器中聚合和更新全局用户分布。
保护用户隐私：全局服务器聚合组件只需输送用户偏好分布的均值和协方差，而不是原始用户-项目评分交互。这样做可以防止恢复原始用户-项目评分交互，同时还可以通过加密方法（如同态加密）来进一步增强安全性。
总之，全局服务器聚合组件的主要功能是聚合和更新用户偏好分布，以解决隐私保护多领域推荐（PPMDR）问题。通过这种聚合和更新，全局服务器聚合组件可以在数据稀疏性问题下提高用户-项目建模的准确性。

用户偏好分布的均值和协方差

均值（Mean）表示用户在不同项目上的平均偏好。均值为向量形式，其中每个元素表示用户对某个项目的偏好。
协方差（Covariance）表示用户在不同项目上的偏好关系。协方差为矩阵形式，其中每个元素表示用户在两个项目上的偏好关系。

(FPPDM++)

++相比普通版本提出了紧凑型聚类的策略。
在论文中，紧凑性聚类的策略是通过两个主要组件实现的：局部领域建模组件和全局服务器聚合组件。局部领域建模组件用于基于用户与物品之间的评分交互来建模用户/物品的概率偏好分布。全局服务器聚合组件旨在收集重叠用户信息以进行知识共享。
为了更好地实现推荐结果，研究人员在FPPDM++中提出了紧凑性聚类方法。该方法旨在利用具有相似喜好和特征的用户进行聚类。同时，利用紧凑性聚类策略还可以进一步减少数据稀疏性问题。
具体来说，紧凑性聚类方法通过以下步骤来实现：

首先，根据领域内用户的相似性，计算用户之间的相似度。
然后，将用户分成M个组，以获得更紧凑的用户表示。
接下来，利用熵-based K-Means方法来确定每个数据与相应聚类之间的关系。
最后，通过最小化局部用户分布与这些聚类分布之间的距离，缩小局部用户分布与聚类分布之间的距离。
通过紧凑性聚类，具有相似喜好或特征的用户将具有更紧凑的表示。这种策略可以提高模型性能，并提供更准确的推荐结果。
这篇论文使用基于熵的Kmeans聚类方法，这是本文与其他论文看到的一个不一样的地方。
基于熵的聚类方比比普通聚类方法相比，不仅要求聚类中的各个元素相似度尽可能的高，还要求聚类中的点域其他聚类中的点尽可能的相似度低。

实验

实验设置

数据集：介绍了Douban和Amazon两个数据集的详细信息。
基线：列举了比较的最先进模型，包括DARec、DOML、CDRIB、FedMF和PriCDR。
实验设置：描述了实验中的不同任务，如Douban的多领域推荐和Amazon的跨领域推荐任务。
评估指标：用于评估推荐性能的指标，如Top@5和Top@10。
实验过程：描述了实验过程中的五个随机实验并计算平均结果。

分析

本部分主要探讨了FPPDM（联邦概率偏好分布建模）与其几个变体（FPPDM++）在Douban和Amazon数据集上的性能比较。FPPDM++揭示了如何通过利用用户的偏好分布和使用紧凑型共聚簇策略来提高模型性能。
实验结果表明，FPPDM++在两个数据集上均取得了较好的性能，尤其是在保护用户隐私的多领域推荐设置下。此外，FPPDM++与其几个变体的性能进行了比较，以了解每个组件如何对最终性能做出贡献。通过比较不同的实验结果，可以得出FPPDM++在保护用户隐私的同时，能够更好地捕捉用户的偏好，并在多领域推荐挑战中取得较好的性能。

结论

在本文中，提出了一种名为联邦概率偏好分布建模（FPPDM）的方法，用于解决多领域推荐问题。该方法通过将用户和项目的分布建模为高斯分布，并使用联邦学习策略在多个领域之间共享用户的偏好信息。此外，我们还提出了一种具有紧凑性的协同聚类方法，以进一步提高模型性能。通过在Douban和Amazon数据集上的实证研究，我们证明了所提出的方法在保护隐私的同时，能够显著提高推荐效果。