一：Self Consistency

题目: SELF-CONSISTENCY IMPROVES CHAIN OF THOUGHT REASONING IN LANGUAGE MODELS
机构：Google Brain, ICLR 2023
论文: https://arxiv.org/pdf/2203.11171.pdf
任务: 对于复杂问题而言，往往可以从多条推理路径得到最终的答案，因此将原来的CoT贪心解码进行优化，提出一种Self Consistency的解码算法
特点: sample-and-marginalize，投票，能够避免CoT的解码的局部最优以及输出重复，可以视作一种“self-ensemble”，无需训练/标注/微调，很容易与现存的采样算法，比如 temperature sampling， top-k sampling，nucleus sampling即插即用。
前置相关工作：CoT

1.1 方法简介

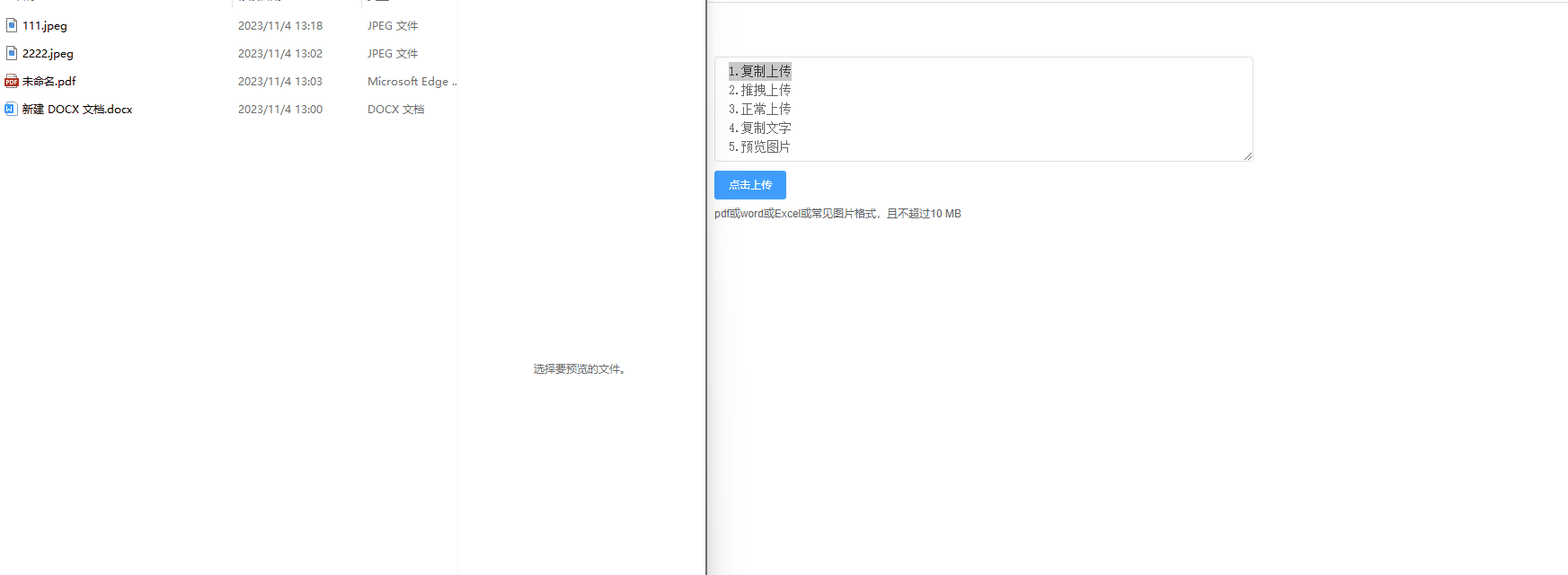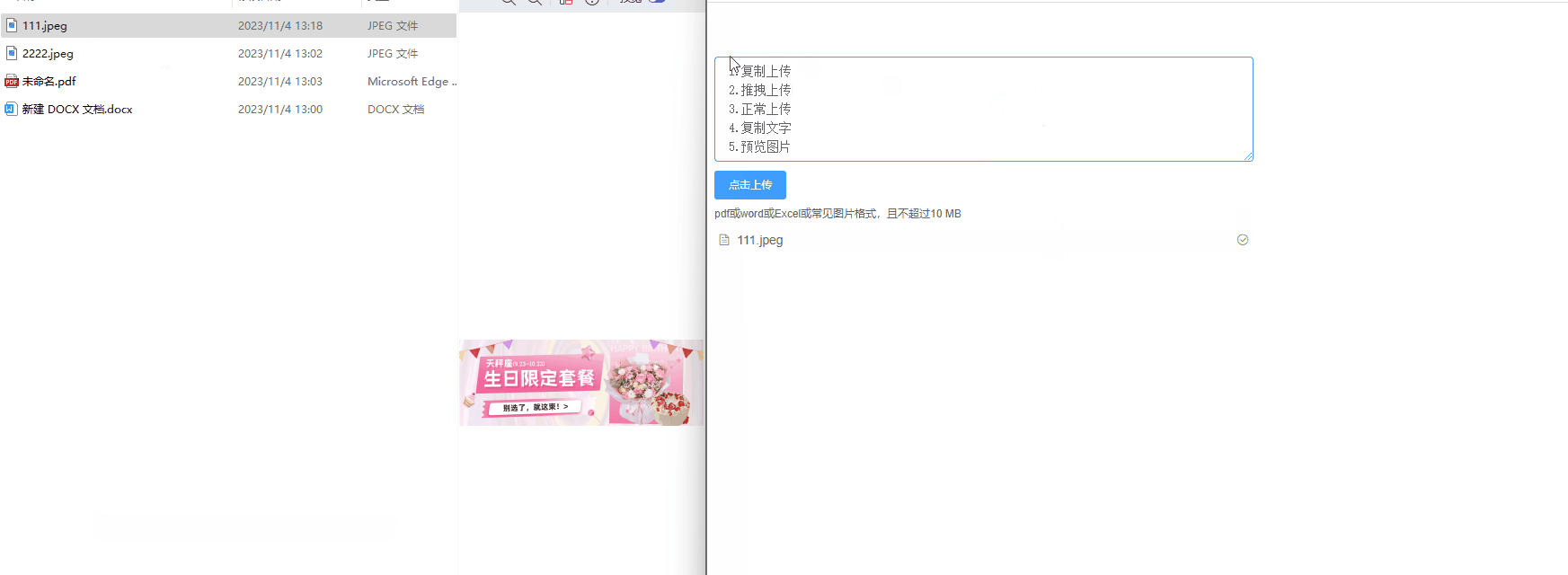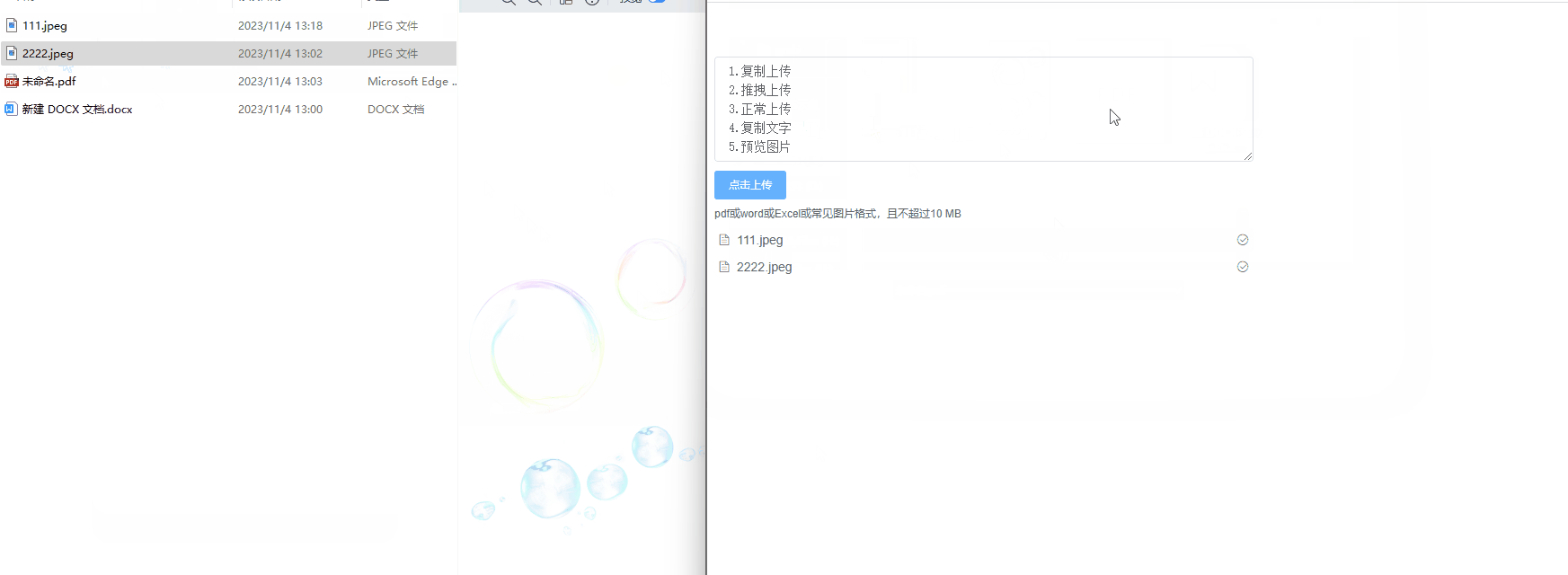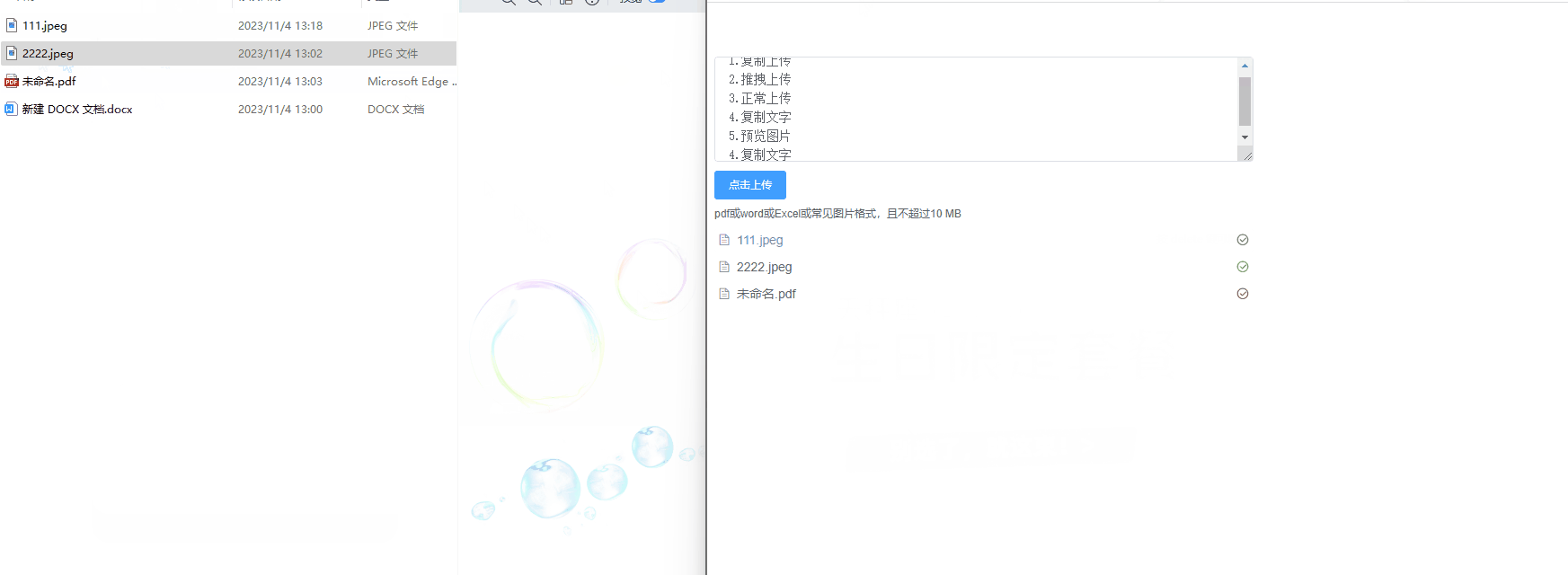
1. 利用CoT prompting大模型
2. 将CoT中的贪心解码替换为采样生成一组推理路径
3. 答案一致性投票

关于NLG的各种采样算法：Greedy Search (Maximization)，Beam Search，Temperature Sampling，Top-K Sampling，Top-P Sampling (Nucleus sampling)，可以参见：

1. https://www.cnblogs.com/miners/p/14950681.html
2. THE CURIOUS CASE OF NEURAL TEXT DeGENERATION

1.2 实验

• Arithmetic Reasoning
• Commonsense and Symbolic Reasoning
• SELF-CONSISTENCY HELPS WHEN CHAIN-OF-THOUGHT HURTS PERFORMANCE
• Comparison to Sample-and-Rank
• Comparison to Beam Search
• Comparison to Ensemble-based Approaches
• Self-Consistency is Robust to Sampling Strategies and Scaling
• Self-Consistency Improves Robustness to Imperfect Prompts
• Self-Consistency Works for Non-Natural-Language Reasoning Paths and Zero-shot CoT

1.3 结果

二：Least-to-most

题目: LEAST-TO-MOST PROMPTING ENABLES COMPLEX REASONING IN LARGE LANGUAGE MODELS
机构：Google Brain, ICLR 2023
论文: https://arxiv.org/pdf/2205.10625.pdf
任务: 为了克服CoT在easy-to-hard示例学习中的泛化性
方法：将复杂的问题分解为一系列的更简单的子问题，然后一个接一个解决，每一个待解决的子问题，都会被上一个已经解决好的子问题的答案促进
特点: 方法中的两个阶段都是通过几次提示（few-shot prompting）来实现的，因此在任何阶段都不需要训练或微调
前置相关工作：CoT，self consistency

2.1 方法简介

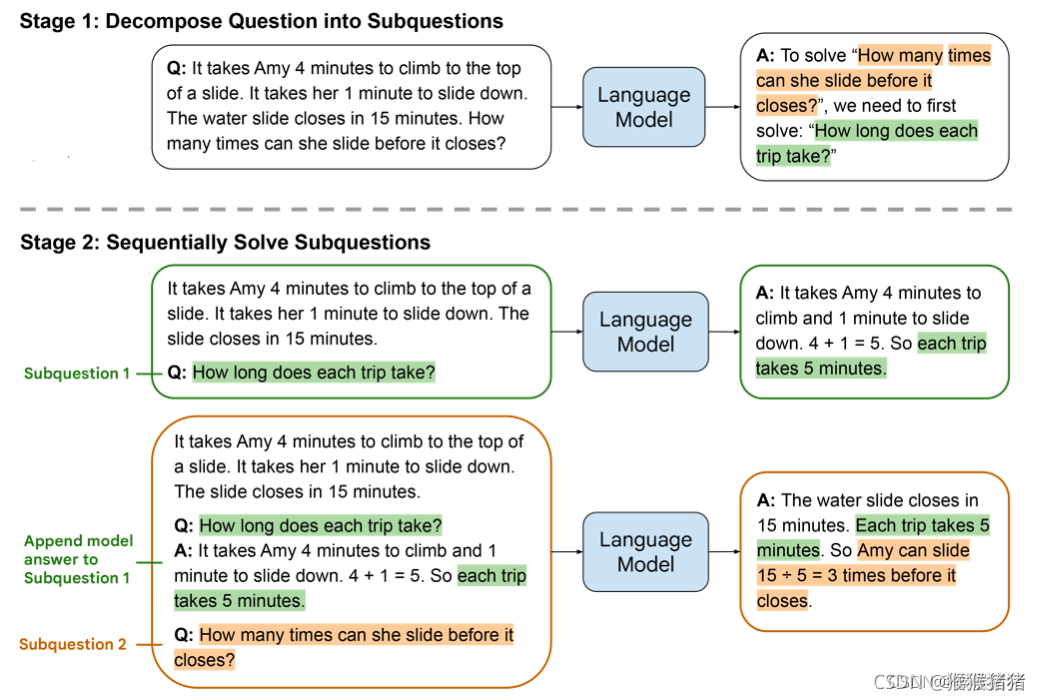
为了解决easy-to-hard的泛化性问题，提出Least-to-most prompting方法，它包含两个阶段：

1. 将一个复杂的问题，分解为一序列简单的子问题
2. 依次解决这些子问题，每一个待解决的子问题，都需要历史已经解决的子问题的答案来促进
   

2.2 示例

该论文在SYMBOLIC MANIPULATION，COMPOSITIONAL GENERALIZATION，MATH REASONING进行了实验，这儿展示MATH REASONING的示例以及结果
Least-to-most样例：

CoT样例：

2.3 结果