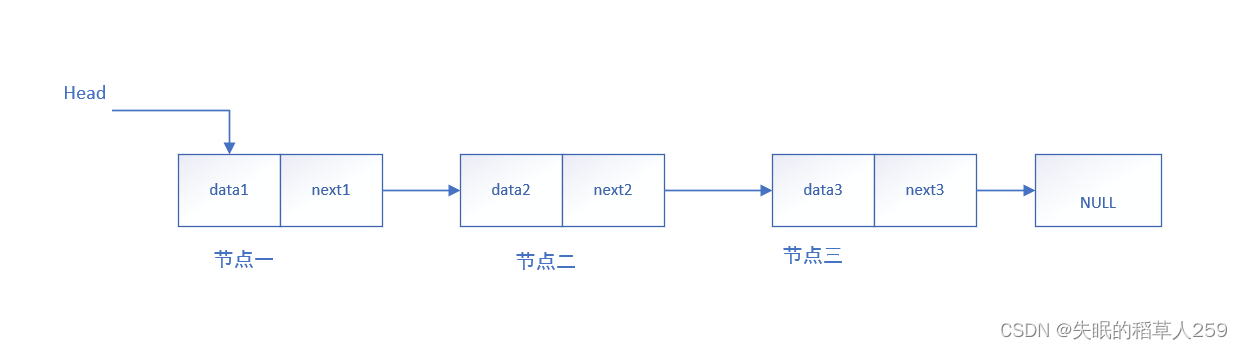
完全二叉树：就是每层横着划过去是连起来的，中间不会断开
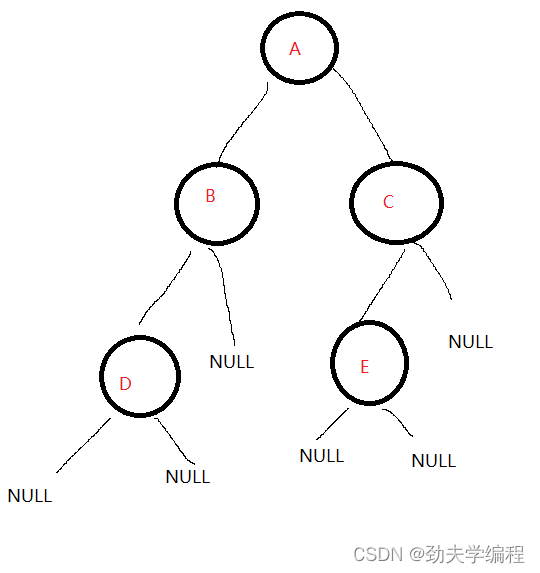
比如下面的左图就是完全二叉树
再比如下面的右图就是非完全二叉树

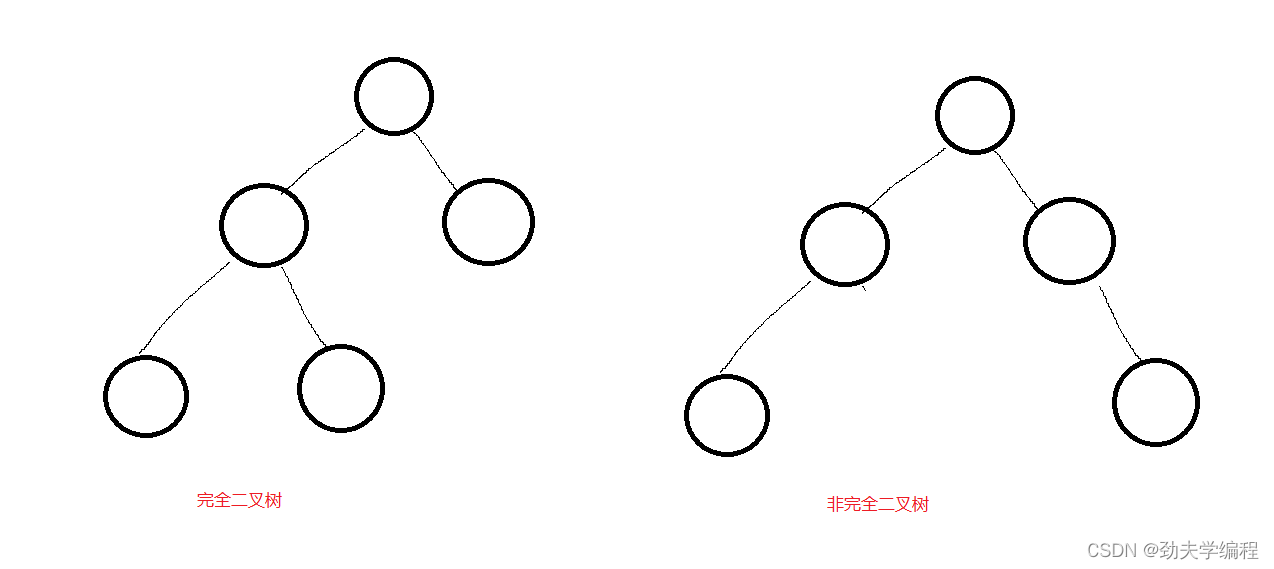
那我们可以采用层序遍历的方法，借助一个辅助队列

当辅助队列不空的时候，出队头元素，入队头元素的左右孩子

这里不同于层序遍历的是，我们这里入左右孩子，如果左右孩子是NULL，我们也入队

当我们在重复执行上面的操作时，我们会有一刻出队列的时候遇到NULL的情况
这时，再对队列的剩余元素进行判断，如果全是NULL则是完全二叉树，否则是非完全二叉树

举例如下

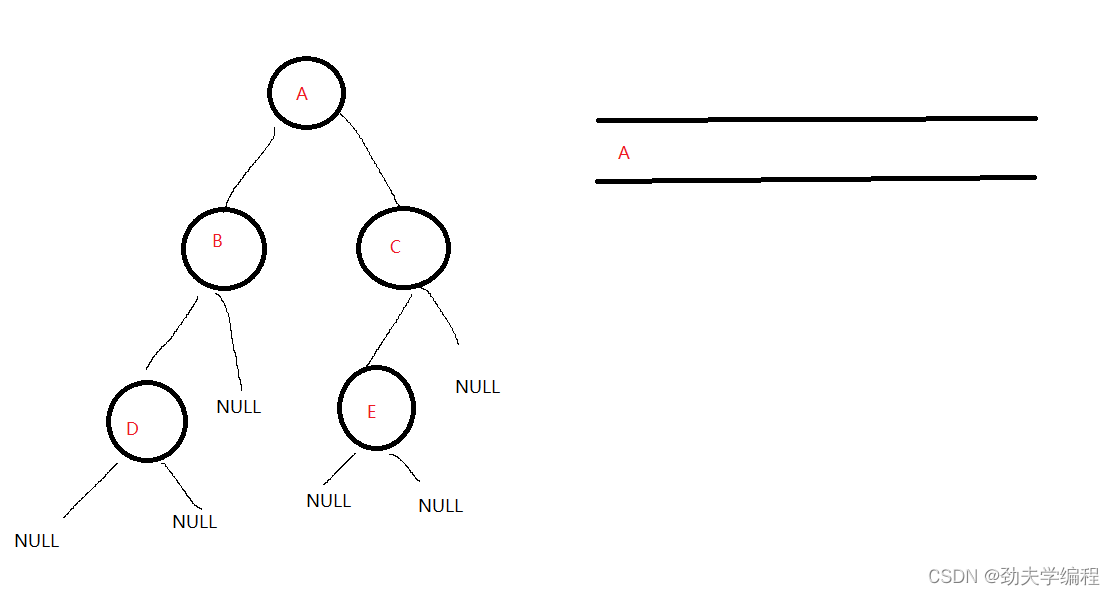
先把根节点A入队

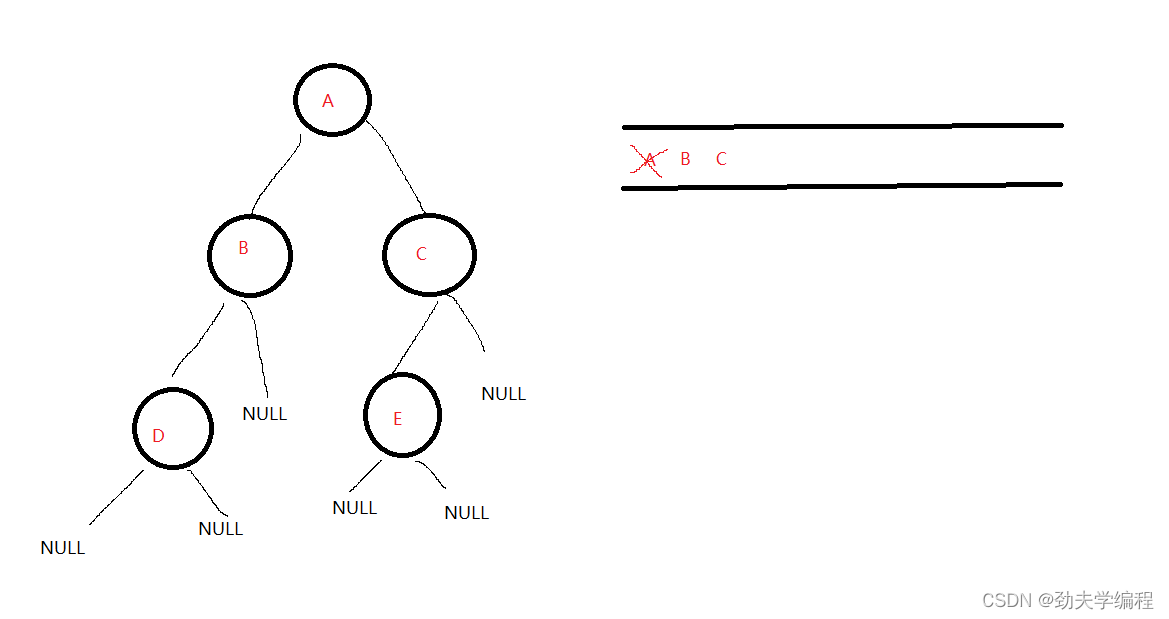
然后队列不空，队头A出队，A的左右孩子BC入队

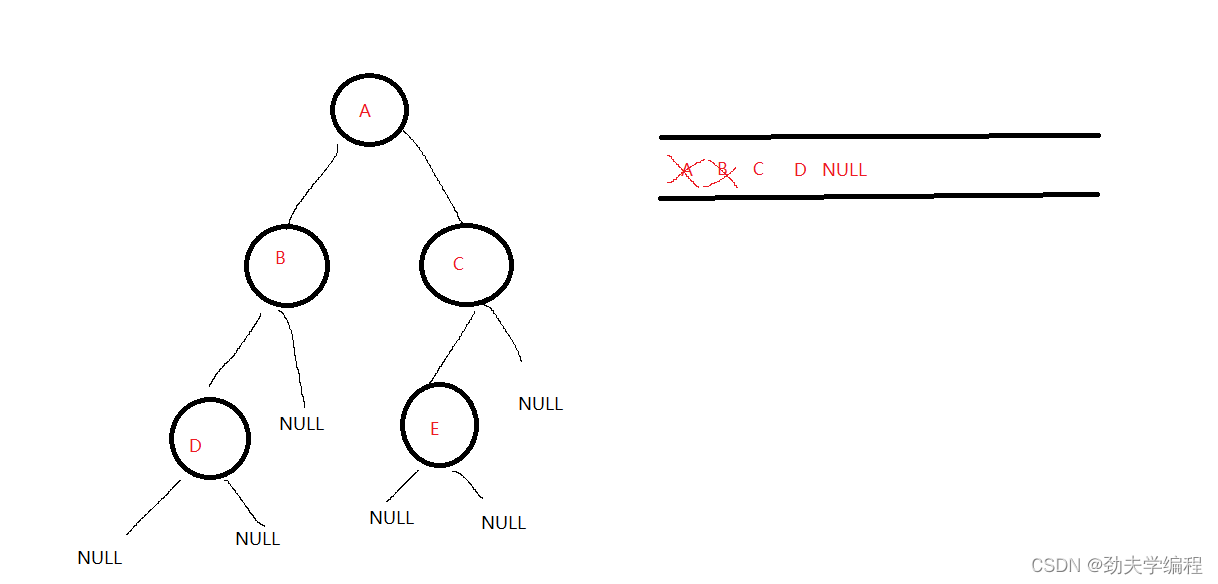
然后队列不空，队头B出队，B的左孩子D 和NULL入队

然后队列不空，队头C出队，C的左右孩子E 和NULL入队

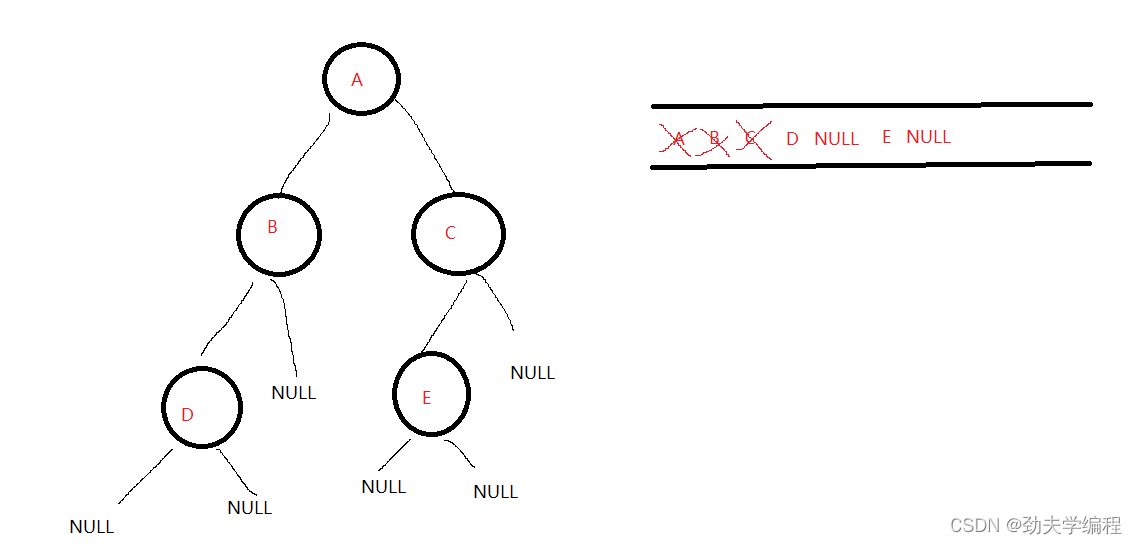
然后队列不空，队头D出队，D的左右孩子NULL入队

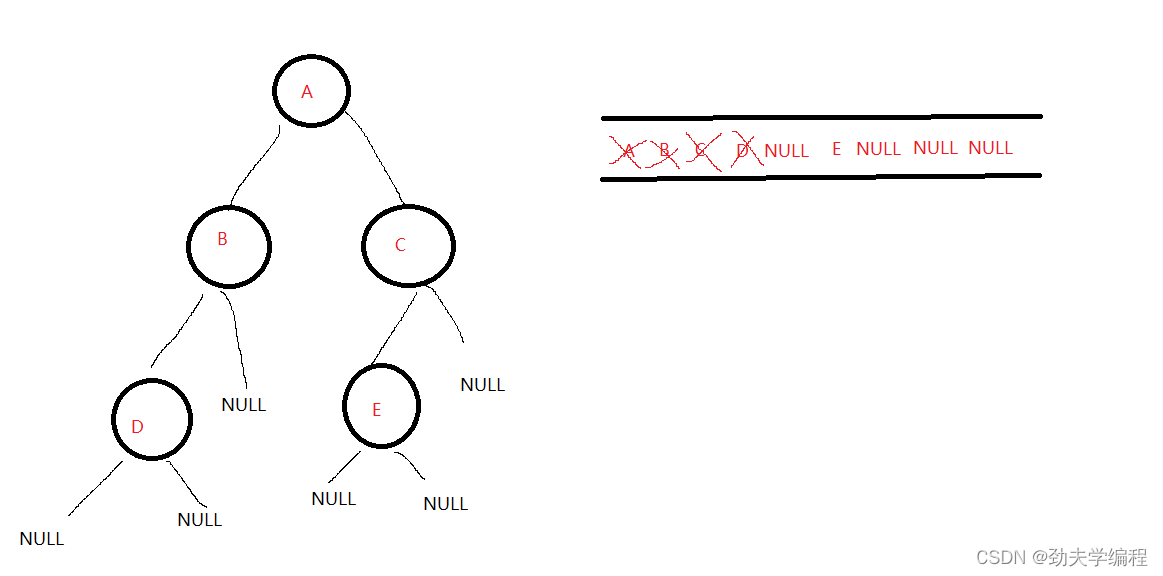
接下来，队不空，出队的元素是NULL
对于这种情况，我们就需要把队列剩余元素看一下了，如果队列剩余元素中有非NULL元素，
那么该树就不是完全二叉树

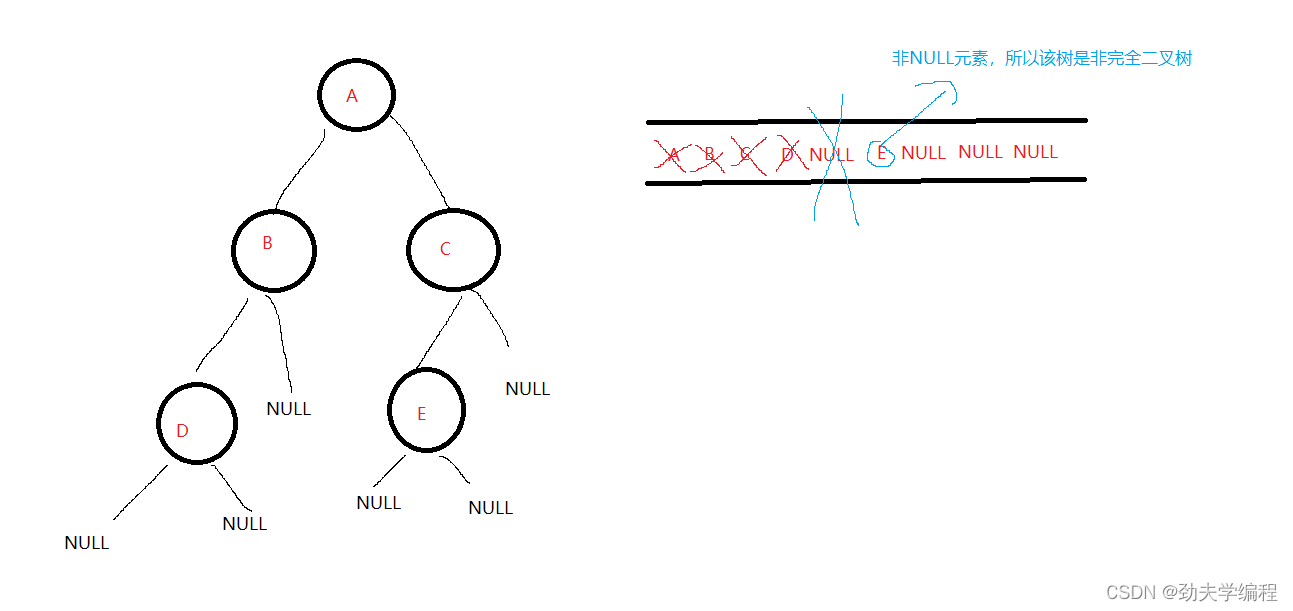
代码如下：

//队列相关操作
void InitQueue(SqQueue* Q);//初始化队列
void EnQueue(SqQueue* Q,BiTree T);//入队
void DeQueue(SqQueue* Q,BiTree* T)//出队头元素，用T带回出队元素
int QueueEmpty(SqQueue Q);//判断队列是否为空

//判断是否是完全二叉树
int IsComplete(BiTree T){
	if(T==NULL){//空树是一种特殊的完全二叉树
		return 1;
	}
	SqQueue Q;//初始化一个辅助队列
	InitQueue(&Q);
	EnQueue(&Q,T);//根节点入队
	while(!QueueEmpty(Q)){//层序遍历
		BiTree p;
		DeQueue(&Q,&p);
		if(p!=NULL){//出的队头元素非空
			//左右孩子入队
			EnQueue(&Q,p->lchild);
			EnQueue(&Q,p->rchild);
		}
		else{//出的队头元素是NULL
			//判断队列中剩余元素是否全是NULL
			//全是NULL——完全二叉树
			//不全是NULL——非完全二叉树
			while(!QueueEmpty(Q)){
				DeQueue(&Q,&p);
				if(p!=NULL){
					return 0;
				}
			}
		}
	}
	return 1;
}