博主主页：Yu·仙笙

专栏地址：洛谷千题详解

 

目录

题目描述

输入格式

输出格式

输入输出样例

解析：

0.0.题意:

1.1.建图

2.2.最短路

C++源码：

C++源码2：

C++源码3：

---

-------------------------------------------------------------------------------------------------------------------------------- 

 

-------------------------------------------------------------------------------------------------------------------------------- 

题目描述

又到暑假了，住在城市 A 的 Car 想和朋友一起去城市旅游。
她知道每个城市都有 44 个飞机场，分别位于一个矩形的 44 个顶点上，同一个城市中两个机场之间有一条笔直的高速铁路，第 ii 个城市中高速铁路了的单位里程价格为 T_iTi​，任意两个不同城市的机场之间均有航线，所有航线单位里程的价格均为 tt。

图例（从上而下）

机场
高速铁路
飞机航线

注意：图中并没有标出所有的铁路与航线。

那么 Car 应如何安排到城市B的路线才能尽可能的节省花费呢?她发现这并不是一个简单的问题，于是她来向你请教。

找出一条从城市 A 到 B 的旅游路线，出发和到达城市中的机场可以任意选取，要求总的花费最少。

-------------------------------------------------------------------------------------------------------------------------------- 

输入格式

第一行为一个正整数 nn，表示有 nn 组测试数据。

每组的第一行有 44 个正整数 s,t,A,Bs,t,A,B。

SS 表示城市的个数，tt 表示飞机单位里程的价格，AA，BB 分别为城市A，B 的序号。

接下来有 SS 行，其中第 ii 行均有 77 个正整数x_{i1},y_{i1},x_{i2},y_{i2},x_{i3},y_{i3},T_ixi1​,yi1​,xi2​,yi2​,xi3​,yi3​,Ti​ ，这当中的 (x_{i1},y_{i1}xi1​,yi1​)，(x_{i2},y_{i2}xi2​,yi2​)，(x_{i3},y_{i3}xi3​,yi3​)分别是第 ii 个城市中任意 33 个机场的坐标，T_iTi​ 为第 ii 个城市高速铁路单位里程的价格。

-------------------------------------------------------------------------------------------------------------------------------- 

输出格式

共有 nn 行，每行 11 个数据对应测试数据。
保留一位小数。

-------------------------------------------------------------------------------------------------------------------------------- 

输入输出样例

输入 #1复制

1
3 10 1 3
1 1 1 3 3 1 30
2 5 7 4 5 2 1
8 6 8 8 11 6 3

输出 #1复制

47.5

-------------------------------------------------------------------------------------------------------------------------------- 

解析：

这个题啊，真是好写，也不好写。

好写呢，在于建个图，再跑一遍FloydFloyd，比较最小值，就没了

不好写呢，就在于：

1.每个矩形只给了3个点.....

2.代码长（可能不是），相近的变量多（这是我）等等

来一步一步分析吧。。。

0.0.题意:

（略）

1.1.建图

(1).(1).找到矩形的另外11个点

这个东西咋找呢？用亿点初中几何知识知道矩形是平行四边形，而平行四边形是对角线互相平分的。

如图所示：

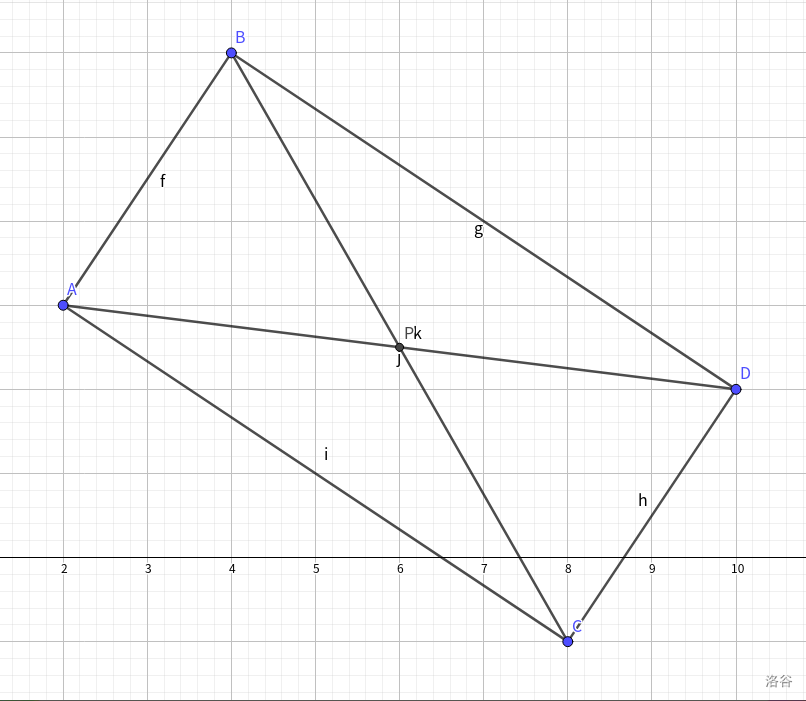
其中，点A,B,CA,B,C为输入的点，DD是所求的点，对角线交点为PP

这个例子中，BCBC是一条对角线，ADAD是另一条。根据中点公式，可以得到

\begin{cases}x_P=\dfrac{x_B+x_C}{2}\\x_P=\dfrac{x_A+x_D}{2}\end{cases}⎩⎪⎨⎪⎧​xP​=2xB​+xC​​xP​=2xA​+xD​​​

\begin{cases}y_P=\dfrac{y_B+y_C}{2}\\y_P=\dfrac{y_A+y_D}{2}\end{cases}⎩⎪⎨⎪⎧​yP​=2yB​+yC​​yP​=2yA​+yD​​​

所以可得

\begin{cases}x_D=x_B+x_C-x_A\\y_D=y_B+y_C-y_A\end{cases}{xD​=xB​+xC​−xA​yD​=yB​+yC​−yA​​

于是， 我们再用勾股定理判断一下哪两个点构成对角线，然后就能求出这个点啦！

(2).(2).建图

这里我们发现题目给了两种路线，一种是城市之间的航空路线，一种是城市内部的公路。

所以建图的主要问题就在于判断两个点是否在同一城市内。

这个问题，要靠你标点的方式确定，此处就举本人的例子来说明。

我的想法是第11个城市标号1,2,3,41,2,3,4,第22个城市标号5,6,7,85,6,7,8,以此类推。

那么这些点的标号与对应的城市号有什么关系呢？

经过研究发现，若点的编号为ii,则它对应的城市编号即为(i-1)/4(i−1)/4（下取整）

于是这样就行了。

2.2.最短路

emmmemmm，一看数据范围，s \leq 100s≤100

所以最多只有400400个点，O(n^3)O(n3)都能过。

那么O(n^3)O(n3)的最短路是啥？FloydFloyd啊~

跑一遍FloydFloyd，然后求一下AA的每个机场到BB的每个机场的最小值就过了~

-------------------------------------------------------------------------------------------------------------------------------- 

C++源码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define f(i,a,b) for(int i=a;i<=b;i++)
const ll inf=0x7f7f7f7f;
ll s,A,B,TTT;
double ans=inf,t,dis[410][410];
double x[410],y[410],T[110];
double diss(double x1,double y1,double x2,double y2){return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));}
double ds(double x1,double y1,double x2,double y2){return (x1-x2)*(x1-x2)+(y1-y2)*(y1-y2);}
int main() {
    scanf("%lld",&TTT);
    while(TTT--){
        memset(dis,0,sizeof(dis)),ans=inf;
        scanf("%lld%lf%lld%lld",&s,&t,&A,&B);
        f(i,1,s){
            scanf("%lf%lf%lf%lf%lf%lf%lf",&x[(i-1)*4+1],&y[(i-1)*4+1],&x[(i-1)*4+2],&y[(i-1)*4+2],&x[(i-1)*4+3],&y[(i-1)*4+3],&T[i]);
            double dab=ds(x[(i-1)*4+1],y[(i-1)*4+1],x[(i-1)*4+2],y[(i-1)*4+2]);
            double dac=ds(x[(i-1)*4+1],y[(i-1)*4+1],x[(i-1)*4+3],y[(i-1)*4+3]);
            double dbc=ds(x[(i-1)*4+2],y[(i-1)*4+2],x[(i-1)*4+3],y[(i-1)*4+3]);
            if(dab+dac==dbc)x[i*4]=x[(i-1)*4+2]+x[(i-1)*4+3]-x[(i-1)*4+1],y[i*4]=y[(i-1)*4+2]+y[(i-1)*4+3]-y[(i-1)*4+1];else
            if(dab+dbc==dac)x[i*4]=x[(i-1)*4+1]+x[(i-1)*4+3]-x[(i-1)*4+2],y[i*4]=y[(i-1)*4+1]+y[(i-1)*4+3]-y[(i-1)*4+2];else
            if(dbc+dac==dab)x[i*4]=x[(i-1)*4+2]+x[(i-1)*4+1]-x[(i-1)*4+3],y[i*4]=y[(i-1)*4+2]+y[(i-1)*4+1]-y[(i-1)*4+3];
        }
        f(i,1,s*4)f(j,1,s*4)if(i!=j){
                if((i-1)/4!=(j-1)/4)dis[i][j]=t*diss(x[i],y[i],x[j],y[j]);
                else dis[i][j]=T[(i-1)/4+1]*diss(x[i],y[i],x[j],y[j]);
            }
        f(k,1,s*4)f(i,1,s*4)f(j,1,s*4)dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
        f(i,1,4)f(j,1,4)ans=min(ans,dis[(A-1)*4+i][(B-1)*4+j]);
        printf("%.1lf\n",ans);
    }
	return 0;
}

-------------------------------------------------------------------------------------------------------------------------------- 

C++源码2：

#include<cstdio>
#include<cmath>
#include<cstring>
#define maxn 200002
#define I return
#define LIKE 0
#define luogu ;
using namespace std;
struct tnode{
    int x,y;
    int city;//x代表城市横坐标，y代表纵坐标，city代表它所属的城市 
}edge[maxn];
int s,t,A,B;
double f[20002];//存火车费用（注意存的是城市里的） 
double fll[1001][1001];//等会儿建图 
double fac(int x) { 
    return x*x; 
}
double distan(int x1, int y1, int x2, int y2) { 
       return 1.0*sqrt(1.0*fac(x1-x2)+1.0*fac(y1-y2)); 
}
void universe(int x1,int y1,int x2,int y2,int x3,int y3,int i) {
    int ab=fac(x1-x2)+fac(y1-y2);
    int bc=fac(x2-x3)+fac(y2-y3);
	int ac=fac(x1-x3)+fac(y1-y3);
    int x4,y4; //求第四个点的坐标，先判断出直角，然后就好办了 
    if (ab+ac==bc) x4=x2+x3-x1, y4=y2+y3-y1;
    if (ab+bc==ac) x4=x1+x3-x2, y4=y1+y3-y2;
    if (bc+ac==ab) x4=x1+x2-x3, y4=y1+y2-y3;
    edge[i+3].x=x4;//存入第四个点里 
    edge[i+3].y=y4;
}
double mon(tnode x1,tnode x2){//读入试先已经准备好微操，所以调用很简单 
	double juli=distan(x1.x,x1.y,x2.x,x2.y);
	if(x1.city==x2.city) return 1.0*juli*f[x1.city];
	return 1.0*juli*t;
}
int main() {
    int n;
	double ans=29292992.0;
    scanf("%d",&n);
    while(n--){
    	memset(fll,98,sizeof(fll));//注意一定是98,(好像没有也没问题） 
        memset(edge,0,sizeof(edge));
        scanf("%d%d%d%d",&s,&t,&A,&B);
        for (int i=1; i<=4*s; i=i+4) {//读入微操，扩展点后，city存储原来的点 
            scanf("%d%d%d%d%d%d%lf",&edge[i].x,&edge[i].y,&edge[i+1].x,&edge[i+1].y,&edge[i+2].x,&edge[i+2].y,&f[i/4+1]);
            edge[i].city=edge[i+1].city=edge[i+2].city=edge[i+3].city=i/4+1;
            universe(edge[i].x,edge[i].y,edge[i+1].x,edge[i+1].y,edge[i+2].x,edge[i+2].y,i);
        }
        for(int i=1;i<=s*4;i++)//建图初始化 
           for(int j=1;j<=s*4;j++)
           	    fll[i][j]=1.0*mon(edge[i],edge[j]);
        for(int k=1;k<=s*4;k++)//标准弗洛伊德 
           for(int i=1;i<=s*4;i++)
              if(i!=k)
              for(int j=1;j<=s*4;j++)
                 if(i!=j&&j!=k){
                 	if(fll[i][j]>fll[i][k]+fll[k][j])
                 	   fll[i][j]=fll[i][k]+fll[k][j];
				}
				//在起点和终点四个点中寻找最小值 
		for(int i=A*4-3;i<=A*4;i++)
		   for(int j=B*4-3;j<=B*4;j++){
		   	  if(fll[i][j]<ans) ans=fll[i][j];
		   }
		printf("%.1lf",ans);
    }
    I LIKE luogu
}

 --------------------------------------------------------------------------------------------------------------------------------

C++源码3：

#include<bits/stdc++.h>
using namespace std;
const int maxn=100005,maxm=500005,inf=0x3f3f3f3f;
double e[1005][1005];
int wz[1005][11];
int n,tf;
double dist(int a,int b,int c,int d){
	return sqrt((a-b)*(a-b)*1.0+1.0*(c-d)*(c-d));
}
double dist1(int a,int b,int c,int d){
	return (a-b)*(a-b)*1.0+1.0*(c-d)*(c-d);
}
int main()
{
	int t;
	cin>>t;
	while(t--)
	{
		int a,b;
		scanf("%d%d%d%d",&n,&tf,&a,&b);
		for(int i=1;i<=4*n;i++)
		  for(int j=1;j<=4*n;j++)
		    e[i][j]=inf;
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=6;j++)
			  scanf("%d",wz[i]+j);
			for(int j=1;j<=5;j+=2)
			{
				wz[i][7]+=wz[i][j];
				wz[i][8]+=wz[i][j+1];
			}
			scanf("%d",wz[i]+9);
			double tp[3];
			int tp2=inf,tp3;
			tp[0]=dist1(wz[i][4],wz[i][6],wz[i][3],wz[i][5]);
			tp[1]=dist1(wz[i][2],wz[i][6],wz[i][1],wz[i][5]);
			tp[2]=dist1(wz[i][2],wz[i][4],wz[i][1],wz[i][3]);
			if(tp[0]+tp[1]==tp[2]){
				wz[i][7]-=2*wz[i][5];wz[i][8]-=2*wz[i][6];
			}
			else if(tp[1]+tp[2]==tp[0]){
				wz[i][7]-=2*wz[i][1];wz[i][8]-=2*wz[i][2];
			}
			else if(tp[0]+tp[2]==tp[1]){
				wz[i][7]-=2*wz[i][3];wz[i][8]-=2*wz[i][4];
			}
		}
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=4;j++)
			  for(int k=j;k<=4;k++)
				{
					int u=(i-1)*4+j,v=(i-1)*4+k;
					double dis=dist(wz[i][j*2-1],wz[i][k*2-1],wz[i][j*2],wz[i][k*2]);
					e[u][v]=e[v][u]=dis*wz[i][9];
				}
		}
		for(int i=1;i<=n;i++)
		  for(int j=1;j<=n;j++)
		    if(i!=j){
		  	for(int k=1;k<=4;k++)
		  	  for(int l=1;l<=4;l++)
		  	    {
		  	    	int u=(i-1)*4+k,v=(j-1)*4+l;
					double dis=dist(wz[i][k*2-1],wz[j][l*2-1],wz[i][k*2],wz[j][l*2]);
					e[u][v]=dis*tf;
				  }
		  }
		for(int k=1;k<=n*4;k++)
		  for(int i=1;i<=n*k;i++)
		    for(int j=1;j<=n*4;j++)
		      if(e[i][j]>e[i][k]+e[k][j])
		          e[i][j]=e[i][k]+e[k][j];
		double ans=inf;
		for(int i=(a-1)*4+1;i<=a*4;i++)
		  for(int j=(b-1)*4+1;j<=b*4;j++)
		    ans=min(ans,e[i][j]);
		printf("%.1lf",ans);
	}
	return 0;
}

  -------------------------------------------------------------------------------------------------------------------------------