【Python】沃罗诺伊图 | KNN 最邻近算法

猛戳！跟哥们一起玩蛇啊 👉 《一起玩蛇》🐍

写在前面：上一章我们介绍了介计算几何领域的德劳内三角剖分，我们提到过关于点集的很多种几何图都与德劳内三角剖分密切相关，其中最具代表的就是我们本章要介绍的 Voronoi 图 (即沃罗诺伊图) 。沃罗诺伊图有许多应用，包括计算机图形学、地理信息系统、计算机视觉等领域。

Ⅰ. 前置知识（Antecedent）

0x00 引入：什么是沃罗诺伊图？

介绍：沃罗诺伊图 (Voronoi Diagram) ，又称 "狄利克雷镶嵌" (Dirichlettessellation) ，又又称泰森多边形 (Thiessen polygon) ，又又又称维诺图。是由俄国数学家格奥尔基 · 沃洛诺伊所建立的空间分割算法，故命名为沃洛诺伊图。

其于1908年提出，在《莫斯科数学学报》上发表了一篇题为《距离函数和近似问题》的论文，在其中首次提出了沃罗诺伊图的概念，沃罗诺伊图后来被广泛应用于许多领域，并成为计算机图形学和地理信息系统等领域的重要工具。

性质：沃洛诺伊图是一种可以把点转化成区域的图表，这种图表中每个划分区域中的任何一点距离区域中心的距离都比距离其他区域中心点的距离更近。

沃罗诺伊图是按照与种子点 (seed point) 的距离分割平面的示意图
对于顶平面上的种子点 $p1,p2,...p_n$ ，根据平面上的点与哪个 $p_i$ 最接近来划分区域

0x01 德劳内三角剖分与沃罗诺伊图的关系

德劳内三角剖分和沃罗诺伊图诺是双重关系 (dual) ，只要知道一个，就可以得到另一个。

德劳内 $\rightarrow$ 沃罗诺伊：

用每个种子点将入口三角分割后，连接被求出的三角形的外接园的中心就是博罗诺可以获得这个图像。

沃罗诺伊 $\rightarrow$ 德劳内：

若将沃罗诺伊区域之间的种子点连接起来，就可以获得这些种子点的德劳内三角剖分。

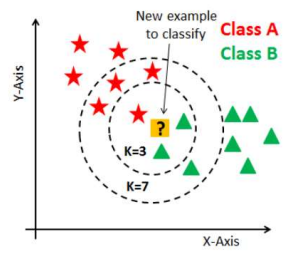
0x02 KNN 最邻近算法 (K-Nearest Neighbor)

(K-Nearest Neighbor)

定义：当输入新数据时，通过将现有数据与新数据进行比较，选出与新数据最接近的 $k$ 个数据，并根据 $k$ 个数据的 category 对输入数据进行分类，通常使用欧几里德距离。

欧几里得距离是两点在 $n$ 维空间中的距离，其公式如下：

$\textrm{KNN}$ 算法的工作流程如下：

确定最近邻数量 $k$ 。
计算待分类样本与训练数据集中每个样本的距离。
按照距离的大小对训练数据集中的样本进行排序。
选取距离最小的 $k$ 个样本。
确定 $k$ 个样本中最多的分类类别。
将待分类样本分类为出现次数最多的类别。

优点：简单高效，学习数据中的噪声影响不大，训练速度可观。

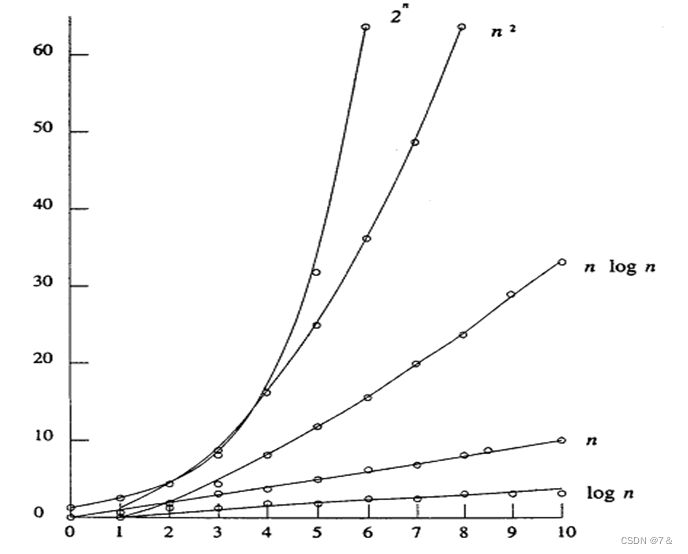
缺点：研究人员根据每个数据的特性任意设置最佳邻域数（ $K$ ）和要使用的距离尺度。测量新的观测值和每个学习数据之间的全部距离，计算耗时较长，对于给定的训练样本集，需要对整个数据集进行扫描，因此时间复杂度为 $O(n)$ ，对于较大的数据集不太适用。

0x03 利用 make_classification 生成分类数据集

我们可以利用 sklearn.datasets 库中的 make_classification 去生成一些数据：

import numpy as np
import matplotlib .pyplot as plt
import cv2
from sklearn.datasets import make_classification

# 使用 make_classification 创建数据
X, y = make_classification (
    n_features = 2,             # 设置特征数为2
    n_samples = 200,            # 设置样本数量为200
    n_informative = 1,          # 指定有用特征数量为1
    n_redundant = 0,            # 指定冗余特征，0为无冗余特征
    n_clusters_per_class = 1,   # 指定每个类别簇数为1
    random_state = 3            # 指定随机数种子为3
)

plt.scatter (
    X[:, 0], X[:, 1],
    marker = 'o', c = y, s = 100, edgecolor = "k", linewidth = 2
)

plt.xlim(-3,3)
plt.ylim(-3,3)
plt.show()

🚩 运行结果：

💡 代码分析：上述代码中， make_classification 函数生成的数据储存在两个变量 $X$ 和 $y$ 中，其中 $X$ 是一个二维数组，包含所有样本的两个特征，而 $y$ 是一个一维数组，包含所有样本的类别。参数解释如下：

n_features 参数用于指定特征数，我们设置为了 2 个。
n_samples 参数用于指定样本数量，我们指定为 200 个。
n_informative 参数指定了有几个特征是有用的（即可以用来帮助分类的），这里设置为 1 表示只有一个特征是有用的。
n_redundant 参数指定了有几个特征是冗余的，这里设置为 0 表示没有冗余特征。
n_clusters_per_class 参数指定了每个类别中有几个簇（cluster），这里设置为 1 表示每个类别只有一个簇。
random_state 参数指定了随机数生成器的种子，可以用来确保生成的数据在不同的运行之间是相同的。

Ⅱ. 沃罗诺伊图（Voronoi Diagram）

0x00 通过 scipy.spatial 生成沃罗诺伊图

最简单的方法就是导入 scipy 库：

from scipy.spatial import Voronoi, voronoi_plot_2d

利用 scipy.spatial.Voronoi 函数生成，并用 scipy.spatial.voronoi_plot_2d 绘制。

from scipy.spatial import Voronoi, voronoi_plot_2d
import matplotlib.pyplot as plt

points = np.random.rand(30, 2)  # 生成随机点集
vor = Voronoi(points)           # 使用Voronoi函数生成
voronoi_plot_2d(vor)            # 绘制

plt.show()

🚩 运行结果： (随机生成)

0x01 基于 make_classification 生成的数据生成沃罗诺伊图

在前置部分我们讲解了如何使用 make_classification 函数生成分类数据集。

现在我们利用刚才该函数生成的数据集，通过 Voronoi 和 voronoi_plot_2d 生成沃罗诺伊图。

💬 代码演示：基于 make_classification 创建的数据生成

import numpy as np
import cv2
import matplotlib .pyplot as plt
from sklearn.datasets import make_classification
from scipy.spatial import Voronoi, voronoi_plot_2d

X, y = make_classification (
    n_features = 2, 
    n_samples = 200, 
    n_informative = 1, 
    n_redundant = 0,
    n_clusters_per_class = 1,
    random_state = 3
)

from scipy.spatial import Voronoi, voronoi_plot_2d

vor = Voronoi(X, qhull_options = 'Qc')   
fig = voronoi_plot_2d(vor)   # 使用 voronoi_plot_2d 生成图
plt.scatter (
    X[:, 0], X[:, 1], 
    marker='o', c=y, s=45, edgecolor="k", linewidth=1 )

plt.show()

🚩 运行结果：

我们还可以尝试使用 annotate 函数给它们标上号：

''' 标号 '''
for i in vor.point_region:
    plt.annotate(str(i), (vor.points[i][0], vor.points[i][1]), size = 12)

0x02 沃罗诺伊图的应用

沃罗诺伊图最重要的条件是，要利用垂直等分线将尽可能接近的两点分割成一定包含一个点的平面，下面我介绍几种能够应用的场景：

寻找最近的便利设施

地图 APP 大家一定使用过，那种 "查看附近" 的功能，就可以运用到沃罗诺伊图。

比如寻找离我所在地最近的医院、药店等便利设施，以我在的地理上的位置为基准点，每个点都可以认为是提供生活所需服务的场所的位置。

病毒传播

流行病学调查中可用于寻找密切接触者，寻找第一个感染者和与他最近接触的人。

疾病感染地区分析

以饮用水泵为基准，划分使用该饮用水泵的人的区域构成。如果某口井被污染了，那么生活在那个领域的人很有可能都喝了被污染的水，可利用这些原理追踪感染源。

……

Ⅲ. 实战练习（Assignment）

练习：KNN & 沃罗诺伊图

Google Colaboratory （K80 GPU）Jupyter Notebook：colab

在 $\textrm{KNN}$ 中保存整个 train set 时，在创建沃罗诺伊图后编辑和推断近邻时，请确保性能相同。

过程：

创建由两个类组成的随机数据使用 sklearn 库的 make_classification 函数
在 $k=1$ 的 $\textrm{KNN}$ 分类器中学习生成的数据 (Classifier1) ，使用 sklearn 库中的 NeighborsClassifier 函数。
使用数据生成全景图
对沃罗诺伊图执行 Nearest Neighbor editing
在 $k=1$ 的 $\textrm{KNN}$ 分类器中学习已编辑数据 (Classifier2)
生成测试数据，比较两个分类器的性能，使用 sklearn 库的 accuratic_score 函数

* 提供基础框架，只需要在 TODO 位置填写代码即可！（完成第一部分和第二部分）

💭 框架提供：base code

第一部分

import numpy as np
import matplotlib .pyplot as plt
import cv2
from sklearn.datasets import make_classification
from scipy.spatial import Voronoi, voronoi_plot_2d

X, y = make_classification(
    n_features=2, n_samples = 200, n_informative=1, n_redundant=0,
    n_clusters_per_class=1, random_state=3)
vor = Voronoi(X, qhull_options = 'Qc')

# 检查图中的邻居，如果只存在与当前类相同的类，则删除当前节点

# 声明要标记是否丢弃的变量
mark = np.zeros(len(X))

# 收集与当前区域相邻的区域的索引信息
# voronoi.ridge_point：存储相邻沃罗诺伊地区的索引。（idx1，idx2）的形式
def get_neighbor_region_idx(curr_idx, voronoi):
    '''
    TODO   在此处添加代码

    '''

    neighbor_pair = []
    for r in voronoi.ridge_points:
        if curr_idx in r:
            neighbor_pair.append(r)
    
    return neighbor_pair


for i in range(len(X)):
    # 收到与当前索引区域相邻的所有区域的信息
    neighbor_pair = get_neighbor_region_idx(i, vor)            
    
    #
    # print(neighbor_pair)
    # Ex ) 
    # [(0, 26), (0, 191), (0, 3), (0, 160), (0, 180), (0, 123), (0, 59)]
    # [(1, 23), (1, 184), (1, 127), (1, 113), (1, 152), (1, 131)]
    # [(2, 93), (2, 74), (2, 33), (2, 13), (2, 103)]
    # ...

    # 距离计算
    shortest_dist = 99999999
    shortest_idx = -1
    
    # 检查所有相邻区域的类
    isSame = True
    for j in range(len(neighbor_pair)):
        idx1 = neighbor_pair[j][0]
        idx2 = neighbor_pair[j][1]
        
        # 比较标签
        if y[idx1]!=y[idx2]: # 如果标签不同
            isSame = False  
            break
                    
    # 如果所有相邻地区都是同一类，则标记。
    # 标记完之后一次性扔掉
    if isSame == True:
        mark[i] = 1
        
# 新的点坐标数组
new_pt = np.where(mark<1)  # 留下未标记的


## 绘图
pt_remain = X[new_pt]
labels_remain = y[new_pt]

plt.scatter(pt_remain[:, 0], pt_remain[:, 1], marker='o', c=labels_remain,
            s=100, edgecolor="k", linewidth=2)
plt.xlim(-3,3)
plt.ylim(-3,3)
plt.show()

🚩 输出效果演示：

第二部分：

from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

test_X, test_y = make_classification (
    n_features=2, n_samples =30, n_informative=1, 
    n_redundant=0, n_clusters_per_class=1, random_state=3)

# 编辑前的数据学习
knn_classifier1 = KNeighborsClassifier(n_neighbors=1)
''' 
TODO   在此处添加代码
'''

y_pred = knn_classifier1.predict(test_X) 
print(f'Accuracy:', (accuracy_score(test_y, y_pred)))


# 编辑后的数据学习
knn_classifier2 = KNeighborsClassifier(n_neighbors=1)
'''
TODO   在此处添加代码
'''

print(f'Accuracy:', (accuracy_score(test_y, y_pred)))

🚩 输出效果演示：

参考答案：

（为了不影响练习，如需查看答案，请自行展开查看）

第一部分：

































knn_classifier1.fit(test_X, test_y)

第二部分：









































knn_classifier2.fit(test_X, test_y)
y_pred = knn_classifier2.predict(test_X)

📌 [ 笔者 ]   王亦优
📃 [ 更新 ]   2022.12.27
❌ [ 勘误 ]   /* 暂无 */
📜 [ 声明 ]   由于作者水平有限，本文有错误和不准确之处在所难免，
              本人也很想知道这些错误，恳望读者批评指正！

📜 参考资料

Microsoft. MSDN(Microsoft Developer Network)[EB/OL]. []. .

百度百科[EB/OL]. []. https://baike.baidu.com/.