1. 简介

堆排序利用的是堆序性，最小堆进行从大到小的排序。
先建初堆，保证堆序性。将堆顶元素与最后一个元素交换，
就将当前堆中的最大(小)的元素放到了最后后。堆大小递减，再重新调整堆选出第二大，重复上述过程。

2. 实现

2.1 建初堆

由于堆具有递归性，即以根节点的所有子树都是一个堆。

我们需要从下往上调整堆。即从完全二叉树的最大非叶子节点开始调整堆，直到根节点。

这样才能保证堆序性。

对于数组3,4,1,2,5 ，建初堆的过程。

• 代码

template<typename T>
void adj_heap(std::vector<T> &arr,std::size_t rt, std::size_t bd) {

    T v = arr[rt];
    std::size_t child;
    std::size_t i;

    for (i = rt; i < bd; i = child) {

        child = i * 2 + 1;
        if ( child + 1 < bd && arr[child + 1] < arr[child])
            ++child;

        if (child >= bd || v <= arr[child] ) {
            break;
        }
        else{
            arr[i] = arr[child];
        }

    }

    arr[i] = v;
}


template<typename T>
void make_orig_heap(std::vector<T> &arr, std::size_t sz) {

    for (std::size_t i = sz/2 - 1; i != -1; --i){
        adj_heap(arr, i, sz);
    }
}

2.2 堆排序

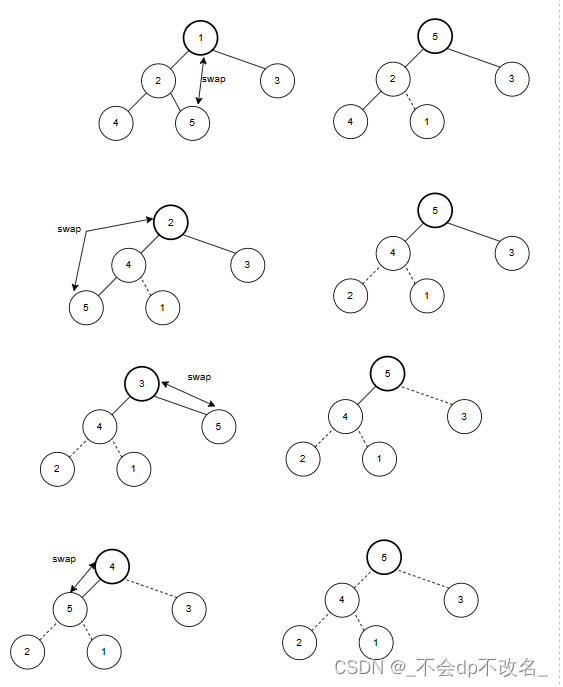
建立初始堆后，我们就确定了最小(大)的元素。

将该元素与最后位置交换，并将堆大小 - 1。

我们就又得到了一个未调整的堆。我们重复调整堆和交换元素的过程，直到最后堆大小为1。

所以，最小堆进行排序形成的序列是从大到小。
过程如图

• 代码

template<typename T>
void heap_sort(std::vector<T> &arr, std::size_t sz) {

    if ( 0 == sz)
        return ;

    make_orig_heap(arr, sz);
    
    

    for (std::size_t i = sz - 1; i > 0; --i) {
        T last = arr[i];
        arr[i] = arr[0];
        arr[0] = last;
        adj_heap(arr, 0, i);
    }

}