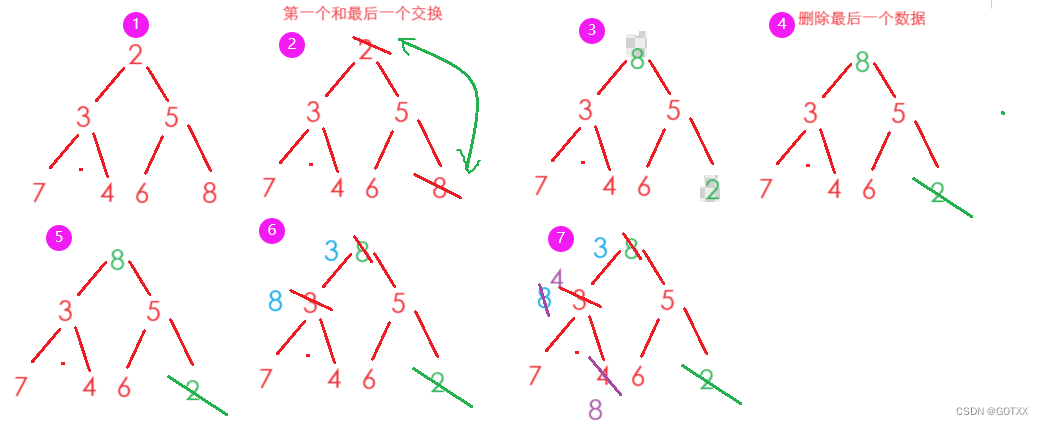
K-means算法
关于K-means算法,它是一种无监督学习算法,用于将数据集分成预定数量的簇(clusters)。
K-means算法比较适合用来做聚类分析,而不是用来预测,换句话来说,K-means算法不擅长预测
K-means算法的主要思想是通过迭代优化来找到最佳簇中心,使得簇内的数据点相似度最大化,而不同簇之间的相似度最小化。
K-means算法的用途
- 市场细分:聚类分析可以帮助企业将其客户细分为不同的市场群体,并了解每个群体的特点和需求。这有助于优化营销策略、定位产品和服务,并更好地满足不同群体的需求。
- 社交网络分析:聚类分析可用于分析社交网络中的群组和社区结构。通过识别具有类似兴趣或行为模式的个体群体,我们可以洞察社交网络的组织结构、影响力传播方式等。
- 生物学分类:聚类分析可以用于生物学中的分类和物种识别。通过对基因组数据、蛋白质序列等进行聚类分析,可以发现相似的生物学特征,并识别出新的物种或基因家族。
- 图像处理:聚类分析可用于图像处理中的分割、聚类或目标检测。通过将像素点聚类到不同的簇中,可以实现图像分割和提取感兴趣的区域。
- 搜索引擎结果分组:聚类分析可以帮助搜索引擎对搜索结果进行分组和聚类。这有助于提供更好的用户体验,将相关结果放在一起,并显示多样性的信息。
- 自然语言处理:聚类分析可以用于文本数据的主题建模、分类和聚类。通过将文档或句子聚类到不同的簇中,可以发现文本之间的相似性和主题结构。
KMeans函数
-
n_clusters:这是KMeans函数的主要参数,指定要将数据集分成的簇的数量。它是一个整数,默认值为8。选择适当的簇的数量是一个重要的任务,可以通过领域知识、经验或使用其他算法进行评估来确定。 -
init:这个参数用于指定簇中心的初始化方法。它有几种可选值:'k-means++'(默认):使用K-means++算法初始化簇中心,以提高聚类效果。'random':随机选择初始簇中心。- 数组:可以传入一个数组作为初始簇中心的位置。
-
n_init:这个参数指定运行K-means算法的次数,每次使用不同的初始簇中心。默认值为10。由于K-means算法对初始簇中心的选择敏感,多次运行可以得到更好的结果。 -
max_iter:这个参数指定算法的最大迭代次数。默认值为300。如果在达到最大迭代次数之前,算法的收敛条件已经满足,则会提前停止。 -
tol:这个参数指定算法的收敛阈值。默认值为1e-4。如果上一次迭代与当前迭代之间的簇中心移动距离小于该阈值,则认为算法已经收敛。 -
random_state:这个参数控制随机数生成器的种子,以确保每次运行时得到相同的结果。通过设置一个固定的随机状态,可以使得结果可重现。除了上述参数,
KMeans函数还有其他一些参数,用于更精细地调整K-means算法的行为。例如,可以使用algorithm参数选择计算簇中心的算法,或者使用precompute_distances参数选择是否预先计算距离等。Kmeans函数的algorithm参数如果不设置
algorithm参数,默认情况下,KMeans函数会根据输入数据的特征数量和样本数量来自动选择最适合的算法。具体地说,如果样本数量较小(少于10000个样本),并且特征数量不高(少于20个特征),则默认使用**"full"算法。这是一种标准的K-means算法,它通过迭代**计算簇中心点的位置,并将每个样本分配到最近的簇中。
另一方面,如果数据集较大或具有高维特征(样本数量大于10000,或特征数量大于等于20),则默认使用"elkan"算法。这种算法在时间效率上比"full"算法更好,因为它利用了矩阵运算的优化技巧来加速计算过程。
总之,默认情况下,在不设置
algorithm参数的情况下,KMeans函数会根据输入数据的规模和特征数量选择最适合的算法进行聚类操作。"full"算法和"elkan"算法都是K-means聚类算法的不同实现方式,它们在计算簇中心点和样本分配上有所不同。
- "full"算法(标准的K-means算法):该算法使用迭代的方式来更新簇中心点和样本分配。它的步骤如下:
- 随机初始化簇中心点。
- 重复以下步骤直到收敛:
- 将每个样本分配到最近的簇中心点。
- 更新每个簇的中心点为该簇中所有样本的均值。
- 返回最终的簇中心点和样本分配结果。
- "elkan"算法(Elkan K-means算法):该算法在"full"算法的基础上进行了优化,通过引入上下界来减少计算量。它的步骤如下:
- 随机初始化簇中心点。
- 计算每个样本到每个簇中心点的距离,并计算每个样本对应的最近簇。
- 重复以下步骤直到收敛:
- 对于每个簇,计算该簇与其他簇之间的距离上界。
- 对于每个样本,如果它的最近簇发生变化,则更新该样本的最近簇。
- 更新每个簇的中心点为该簇中所有样本的均值。
- 返回最终的簇中心点和样本分配结果。
相对于"full"算法,"elkan"算法在计算上具有更高的效率,特别是对于大规模数据集和高维数据。它通过引入上下界的计算,避免了不必要的距离计算,从而提高了聚类的速度。因此,当处理较大规模或高维数据时,推荐使用"elkan"算法来加速K-means聚类过程。
from sklearn.cluster import KMeans # 创建模型对象,并指定algorithm参数为"elkan" model = KMeans(n_clusters=3, algorithm='elkan') # 训练模型 model.fit(X_train) # 使用模型进行预测 y_pred = model.predict(X_test) # 打印预测结果 print(y_pred) - "full"算法(标准的K-means算法):该算法使用迭代的方式来更新簇中心点和样本分配。它的步骤如下:
fit函数和predict函数
fit函数
fit()函数:
fit()函数用于对数据集进行聚类分析。它接受输入数据集作为参数,并在数据上执行迭代过程来找到最佳的簇中心点。- 算法开始时,随机选择k个簇中心点(根据用户指定的簇数k),然后通过迭代的方式优化这些中心点的位置,使得每个数据点都与离其最近的簇中心点关联。
- 迭代过程中,算法会反复计算每个数据点与簇中心点之间的距离,并将每个数据点分配给距离最近的簇中心点。
- 最终,算法会更新簇中心点的位置,以使得它们成为簇内所有数据点的平均值。然后,迭代过程继续,直到达到收敛条件(例如,簇中心点不再发生显著变化或达到最大迭代次数)。
from sklearn.cluster import KMeans
import numpy as np
# 创建一个Kmeans模型对象
model = KMeans(n_clusters=3, random_state=42)
# 准备训练数据
X_train = np.array([[1, 2], [1, 4], [1, 0],
[4, 2], [4, 4], [4, 0]]) # 输入特征矩阵
# 使用Fit函数训练模型
model.fit(X_train)
代码解释
-
导入库和模块:
pythonCopy Codefrom sklearn.cluster import KMeans import numpy as np首先,我们导入了所需的库和模块。
sklearn.cluster中包含了用于聚类任务的K-Means类,numpy库用于处理数组和矩阵。 -
创建K-Means模型对象:
pythonCopy Codemodel = KMeans(n_clusters=3, random_state=42)在这一步,我们创建了一个K-Means模型对象
model。通过指定参数n_clusters=3,我们告诉模型将数据聚类为3个簇。random_state=42用于设置随机种子,以确保结果的可重复性。 -
准备训练数据:
pythonCopy CodeX_train = np.array([[1, 2], [1, 4], [1, 0], [4, 2], [4, 4], [4, 0]])这一步中,我们创建了一个包含训练数据的特征矩阵
X_train。该矩阵包含6个样本,每个样本有2个特征。 -
训练模型:
pythonCopy Codemodel.fit(X_train)使用
fit()函数来训练模型。在这个步骤中,模型将根据输入数据X_train来调整其内部参数,以实现数据的聚类。训练过程中,K-Means算法会通过迭代的方式计算簇中心点,并将样本分配到最近的簇中。在训练过程中,K-Means算法会迭代多次,直到达到指定的停止条件(例如最大迭代次数或簇中心点的变化小于阈值)。
完成以上步骤后,模型就已经训练完毕。现在可以使用该模型进行聚类预测,或者对新的未知数据进行分类。
predict函数
predict()函数:
predict()函数用于将新样本点分配到训练好的簇中心点所属的簇。- 在
fit()函数完成后,我们可以使用predict()函数将新的未知样本点分配给最近的簇中心点。 - 这个过程涉及计算新样本点与每个簇中心点之间的距离,并返回最近的簇中心点的标签或索引
# 准备测试数据
X_test = [[6], [7], [8]] # 输入特征矩阵
# 使用Predict函数进行预测
y_pred = model.predict(X_test)
print(y_pred) # 输出预测结果
代码解释
-
准备测试数据:
pythonCopy CodeX_test = np.array([[0, 0], [4, 4]])在这个步骤中,我们创建了一个包含2个测试样本的特征矩阵
X_test。这些样本是新的未知数据,我们将使用模型来对它们进行聚类预测。 -
预测结果:
pythonCopy Codey_pred = model.predict(X_test)使用
predict()函数来对测试数据进行聚类预测。在这个步骤中,模型将使用之前训练过的簇中心点来计算测试样本所属的簇,然后将其分配到最近的簇中。这个过程通常被称为“标签传播”。预测过程完成后,输出结果存储在变量
y_pred中。在这个例子中,y_pred将包含2个标签,分别表示两个测试样本所属的簇编号。 -
打印预测结果:
pythonCopy Codeprint(y_pred)最后,我们打印了预测结果
y_pred。在这个例子中,输出结果应该是一个包含2个整数的Numpy数组,例如[2 1]。这意味着第一个测试样本被分配到第3个簇中,第二个测试样本被分配到第2个簇中。
结果解释
在K-means聚类算法中,每个簇都有一个唯一的编号,从0开始递增。在这个例子中,我们将数据划分为3个簇,因此它们的编号分别为0、1和2。
当使用predict()函数对测试数据进行预测时,模型会计算每个测试样本到每个簇中心点的距离,并将样本分配到最近的簇中。在这个过程中,每个分配的簇都有一个唯一的编号,就是该簇在训练集中的编号。
在本例中,第一个测试样本[0, 0]距离第3个簇中心点最近,因此被分配到编号为2的簇中。同样,第二个测试样本[4, 4]距离第2个簇中心点最近,因此被分配到编号为1的簇中。所以输出的结果是[2, 1],表示第一个测试样本属于编号为2的簇,第二个测试样本属于编号为1的簇。
其他常用函数\属性
kmeans.cluster_centers_: 这个属性返回每个簇的中心点。可以通过查看这些中心点来了解各个簇的特征。kmeans.labels_: 这个属性返回每个样本的标签,即所属的簇的索引。可以通过查看样本的标签来了解样本被分到了哪个簇。
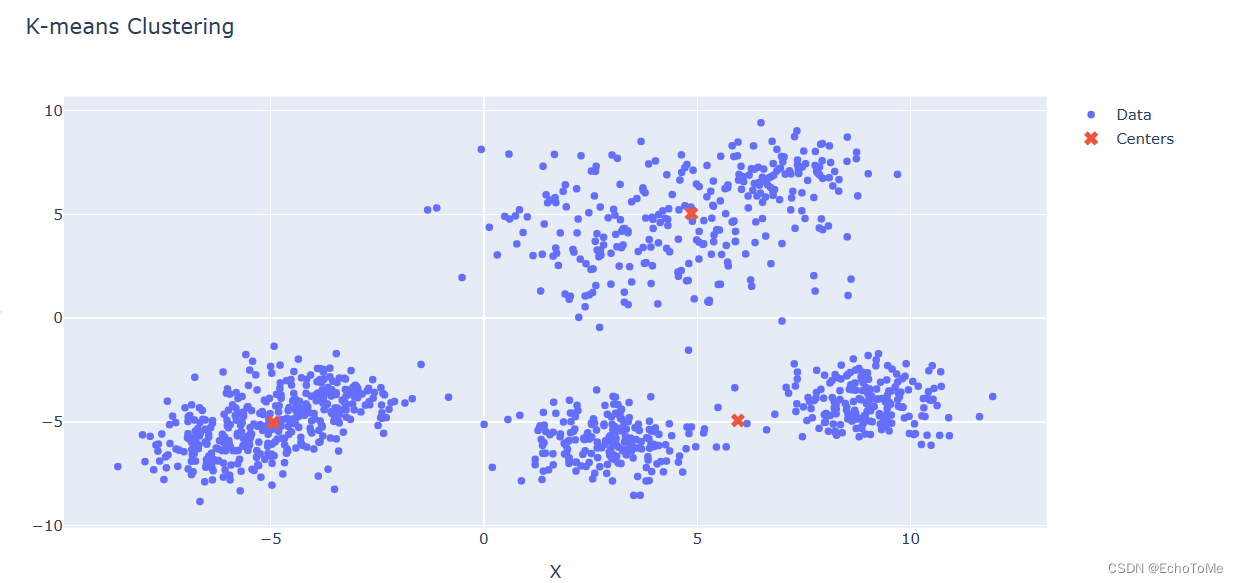
例子
import numpy as np
import plotly.graph_objects as go
from sklearn.cluster import KMeans
# 创建一个包含三个不同形状的二维数据集
np.random.seed(0)
# 第一个形状为圆形的数据集
circle = np.random.randn(200, 2) * 2 + np.array([4, 4])
inner_circle = np.random.randn(100, 2) + np.array([7, 7])
data1 = np.vstack((circle, inner_circle))
# 第二个形状为月牙形的数据集
moon1 = np.random.randn(200, 2) + np.array([-6, -6])
moon2 = np.random.randn(200, 2) + np.array([-4, -4])
data2 = np.vstack((moon1, moon2))
# 第三个形状为矩形的数据集
rect1 = np.random.randn(200, 2) + np.array([3, -6])
rect2 = np.random.randn(200, 2) + np.array([9, -4])
data3 = np.vstack((rect1, rect2))
# 将三个数据集合并为一个数据集
data = np.vstack((data1, data2, data3))
# 使用K-means算法进行聚类
kmeans = KMeans(n_clusters=3, random_state=0)
kmeans.fit(data)
# 获取聚类结果和簇中心
labels = kmeans.labels_
centers = kmeans.cluster_centers_
# 创建可交互的散点图
fig = go.Figure()
# 绘制原始数据
fig.add_trace(go.Scatter(x=data[:, 0], y=data[:, 1], mode='markers', name='Data'))
# 绘制簇中心
fig.add_trace(go.Scatter(x=centers[:, 0], y=centers[:, 1], mode='markers', marker=dict(symbol='x', size=10), name='Centers'))
# 设置布局和标题
fig.update_layout(title='K-means Clustering', xaxis_title='X', yaxis_title='Y')
# 显示图形
fig.show()