🎃个人专栏：

🐬 算法设计与分析：算法设计与分析_IT闫的博客-CSDN博客

🐳Java基础：Java基础_IT闫的博客-CSDN博客

🐋c语言：c语言_IT闫的博客-CSDN博客

🐟MySQL：数据结构_IT闫的博客-CSDN博客

🐠数据结构：​​​​​​数据结构_IT闫的博客-CSDN博客

💎C++：C++_IT闫的博客-CSDN博客

🥽C51单片机：C51单片机（STC89C516）_IT闫的博客-CSDN博客

💻基于HTML5的网页设计及应用：基于HTML5的网页设计及应用_IT闫的博客-CSDN博客​​​​​​

🥏python：python_IT闫的博客-CSDN博客

欢迎收看，希望对大家有用！

目录

🎯目的：

🎯内容：

🎯环境：

🎯步骤：

🥏折半查找：

 💛主要代码解析：

💻完整代码：

 🥏二叉排序树：

 💛主要代码解析：

 💻完整代码：

---

🎯目的：

1、掌握查找的特点。

2、掌握折半查找的基本思想及其算法。

3、熟悉二叉排序树的特点，掌握二叉排序树的插入、删除操作。

🎯内容：

1、设有关键字序列，使用折半查找的方法查找关键字是否存在。

2、根据关键字序列构造二叉排序树，并完成插入、删除关键字的操作。

🎯环境：

TC或VC++。

🎯步骤：

🥏折半查找：

 💛主要代码解析：

1. #include <iostream>、#include <string>、#include <vector>：这些是预处理指令，用于引入标准库的头文件，以便在程序中使用相应的功能。

2. using namespace std;：这是一个命名空间的声明，它允许在代码中直接使用std命名空间中的标识符，而无需在前面加上std::前缀。

3. typedef string KeyType;、typedef int InfoType;：这些是类型定义语句，用于给已有类型（string和int）起别名，便于在代码中使用。

4. struct ElemType { ... };：这是一个结构体定义，用于表示数据元素类型。每个数据元素包含一个关键字和其他信息域。

5. struct SeqList { ... };：这是一个结构体定义，用于表示顺序表类型。顺序表包含一个存储空间的基地址和当前长度。

6. int binary_search(SeqList& list, int target_score) { ... }：这是一个折半查找函数的定义，用于在顺序表中查找目标成绩，并返回其位置。函数使用二分法进行查找。

7. int main() { ... }：这是程序的主函数，程序从这里开始执行。

8. 创建顺序表并初始化：程序中创建了一个顺序表对象list，通过new运算符动态分配了一个能容纳6个数据元素的数组，并将其地址赋给list.R，同时设置list.length为6。该顺序表存储了6个学生的姓名和成绩信息。

9. 输出所有学生成绩：通过for循环遍历顺序表中的所有数据元素，并使用cout流输出每个学生的姓名和成绩信息。

10. 从键盘输入要查找的成绩：使用cin流从控制台接收用户输入的目标成绩。

11. 调用折半查找函数进行查找：调用binary_search函数，在顺序表中使用折半查找算法查找与目标成绩匹配的学生信息，并返回其位置。

12. 根据查找结果输出相应信息：根据查找的结果，使用条件语句判断是否找到了匹配的学生信息，并将结果输出到控制台。

13. 从键盘输入要查找的姓名：使用cin流从控制台接收用户输入的目标姓名。

14. 在顺序表中查找姓名：通过for循环遍历顺序表中的所有数据元素，查找与目标姓名匹配的学生信息，并记录其位置。

15. 根据查找结果输出相应信息：根据查找的结果，使用条件语句判断是否找到了匹配的学生信息，并将结果输出到控制台。

（1）使用顺序存储法存储若干个学生的成绩，例如：从键盘输入ava 35 , emy 57 , jack 62 , lily 71 , lucy 83 , mary 90，并输出其值；

（2）从键盘输入71，查找是否存在该成绩，若存在，则输出该成绩对应在表中的所有信息，否则给出查找失败的信息；

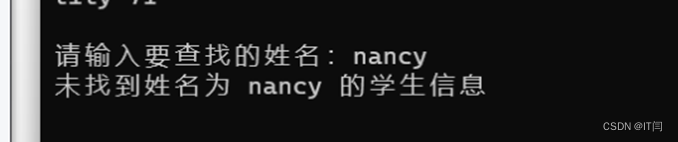
（3）从键盘输入nancy，查找是否存在该姓名，若存在，则输出该姓名对应在表中的所有信息，否则给出查找失败的信息。

💻完整代码：

/*如果此程序运行不成功，请您做以下操作
 工具–编译选项—编译器
勾选编译时加入以下命令
并加入下面代码：-std=c++11
 */
#include <iostream>
#include <string>
#include <vector>

using namespace std;

typedef string KeyType;
typedef int InfoType;

// 数据元素类型定义
struct ElemType {
    KeyType key;        // 关键字域
    InfoType otherinfo; // 其他域
};

// 顺序表的定义
struct SeqList {
    ElemType* R;   // 储存空间的基地址
    int length;    // 当前长度
};

// 折半查找函数，返回查找到的位置，若未找到，返回 -1
int binary_search(SeqList& list, int target_score) {
    int left = 0;
    int right = list.length - 1;
    while (left <= right) {
        int mid = (left + right) / 2;
        if (list.R[mid].otherinfo == target_score) {
            return mid;
        } else if (list.R[mid].otherinfo < target_score) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    return -1;
}

int main() {
    // 从键盘输入若干个学生成绩，并将其存储在顺序表中
    SeqList list = {new ElemType[6], 6};
    list.R[0] = {"ava", 35};
    list.R[1] = {"emy", 57};
    list.R[2] = {"jack", 62};
    list.R[3] = {"lily", 71};
    list.R[4] = {"lucy", 83};
    list.R[5] = {"mary", 90};

    // 输出所有学生成绩
    cout << "所有学生成绩：\n";
    for (int i = 0; i < list.length; ++i) {
        cout << list.R[i].key << " " << list.R[i].otherinfo << endl;
    }
    cout << endl;

    // 从键盘输入要查找的成绩
    int target_score;
    cout << "请输入要查找的成绩：";
    cin >> target_score;

    // 查找成绩为 target_score 的学生信息并输出
    int pos = binary_search(list, target_score);
    if (pos != -1) {
        cout << "成绩为 " << target_score << " 的学生信息：\n";
        cout << list.R[pos].key << " " << list.R[pos].otherinfo << endl;
    } else {
        cout << "未找到成绩为 " << target_score << " 的学生信息\n";
    }
    cout << endl;

    // 从键盘输入要查找的姓名
    string target_name;
    cout << "请输入要查找的姓名：";
    cin >> target_name;

    // 查找姓名为 target_name 的学生信息并输出
    pos = -1;
    for (int i = 0; i < list.length; ++i) {
        if (list.R[i].key == target_name) {
            pos = i;
            break;
        }
    }
    if (pos != -1) {
        cout << "姓名为 " << target_name << " 的学生信息：\n";
        cout << list.R[pos].key << " " << list.R[pos].otherinfo << endl;
    } else {
        cout << "未找到姓名为 " << target_name << " 的学生信息\n";
    }

    return 0;
}

 🥏二叉排序树：

 💛主要代码解析：

这段代码是关于二叉排序树的实现。下面是对代码的解析：

1. 定义了三个类型：
   - KeyType：表示关键字的类型，这里定义为int。
   - InfoType：表示其他数据项的类型，这里定义为int。
   - ElemType：表示二叉排序树中每个节点的数据域类型，包括一个关键字项和其他数据项。

2. 定义了二叉排序树的节点结构BSTNode，包括数据域data和左右孩子指针lchild、rchild。

3. 定义了二叉排序树的指针类型BSTree，即指向BSTNode的指针。

4. 实现了二叉树的插入操作InsertBST：
   - 如果二叉树为空，则生成一个新的节点S，并将关键字key赋值给S的data.key，然后将S作为叶子节点插入到树中。
   - 如果key小于当前节点的关键字，则在左子树上继续递归地插入。
   - 如果key大于当前节点的关键字，则在右子树上继续递归地插入。

5. 实现了二叉树的创建操作CreatBST：
   - 首先将树T初始化为空树。
   - 然后依次读入关键字为key的节点，将每个节点插入到二叉排序树T中，直到输入-1结束。

6. 实现了二叉树的查找操作SearchBST：
   - 如果当前节点为空或者当前节点的关键字等于要查找的关键字key，则返回当前节点的指针。
   - 如果key小于当前节点的关键字，则在左子树上继续递归地查找。
   - 如果key大于当前节点的关键字，则在右子树上继续递归地查找。

7. 实现了中序遍历操作InOrderTraverse：
   - 如果当前节点不为空，先递归遍历左子树，然后输出当前节点的关键字，最后递归遍历右子树。

8. 在主函数main中：
   - 创建一个空的二叉排序树T，并通过CreatBST函数将输入的整数构建成二叉排序树。
   - 输出中序遍历结果。
   - 插入数据元素13，并再次输出中序遍历结果。
   - 查找数据元素37，如果不存在则插入，并输出结果。
   - 查找数据元素20，如果不存在则插入，并输出结果。
   - 最后输出查找37和20后的中序遍历结果。

总结：这段代码实现了二叉排序树的插入、创建、查找和中序遍历操作。它可以构建一个有序的二叉树，并能够快速查找和插入元素。

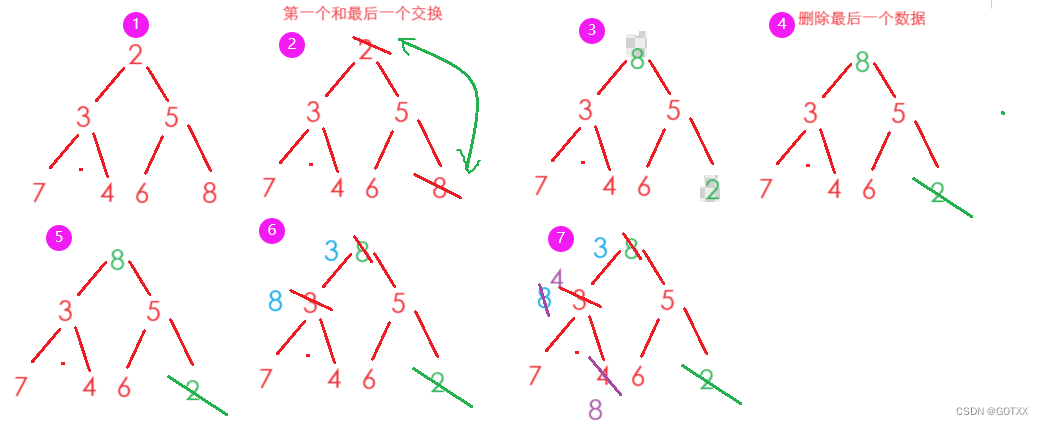
（1）二叉排序树结点定义；

（2）从键盘上输入六个整数45、24、53、12、37、9构造二叉排序树；

（3）输出其中序遍历结果；

（4）插入数据元素13，输出其中序遍历结果；

（5）查找数据37和20是否存在，若存在输出提示，若不存在，则将该数据插入二叉排序树中；

 💻完整代码：

#include "iostream"
using namespace std;
typedef int KeyType;
typedef int InfoType;
typedef int Elemtype;

//二叉排序树的二叉链表储存表示
typedef struct{
	KeyType key;//关键字项 
	InfoType otherinfo;//其他数据项 
}ElemType;//每个结点的数据域的类型
typedef struct BSTNode{
	ElemType data;//每个结点的数据域包括关键字和其他数据域
	struct BSTNode *lchild,*rchild;//左右孩子指针 
}BSTNode,*BSTree;

//二叉树的插入
void InsertBST(BSTree &T,KeyType key){
	//当二叉树不存在关键字等于e.key时，则插入
	if(!T){
		BSTree S;
		S=new BSTNode;//生成新的结点*S
		S->data.key=key;
		S->lchild=S->rchild=NULL;//把结点S作为叶子结点
		T=S;//把S插入到找到的位置 
	} 
	else if(key<T->data.key)
		InsertBST(T->lchild,key);//插入到左子树 
	else if(key>T->data.key)
		InsertBST(T->rchild,key);//插入到右子树 
} 

//二叉树的创建
void CreatBST(BSTree &T){//依次读入关键字为的结点，将相应的结点插入到二叉排序树T中
	T=NULL;//将二叉排序树T初始化为空树
	ElemType e;
	cin>>e.key;
	while(e.key!=-1){//以-1结束 
		InsertBST(T,e.key);
		cin>>e.key;
	} 
}

//二叉树的查找 
BSTree SearchBST(BSTree T,KeyType key){
	//查找成功，返回节点指针：查找失败，返回空指针 
	if((!T)||key==T->data.key) 
		return T;//如果为空树或查找成功
	else if(key<T->data.key)
		return SearchBST(T->lchild,key);//在左子树上找 
	else
		return SearchBST(T->rchild,key);//在右子树上找 
}

void InOrderTraverse(BSTree T){//中序遍历输出
	if(T){
		InOrderTraverse(T->lchild);//遍历左子树 
		cout<<T->data.key<<" ";
		InOrderTraverse(T->rchild);//遍历右子树 
	} 
}

int main(){
	BSTree T; 
	KeyType key;
	ElemType e;
	cout<<"请您输入整数构建二叉排序树(以-1结尾)"<<endl; 
	CreatBST(T);
	cout<<"中序遍历为："<<endl;
	InOrderTraverse(T);
	cout<<"\n插入数据元素13后，遍历结果为："<<endl;
	InsertBST(T,13);
	InOrderTraverse(T);
	if(!SearchBST(T,37)){
		cout<<"\n数据元素37不存在,已将其插入树中"<<endl; 
		InsertBST(T,37);
	}else{
		cout<<"\n数据元素37已存在"<<endl; 
	}
	if(!SearchBST(T,20)){
		cout<<"数据元素20不存在,已将其插入树中"<<endl;
		InsertBST(T,20);
	}else{
		cout<<"\n数据元素20已存在"<<endl;
	}
	cout<<"查找37和20后，遍历结果为："<<endl;
	InOrderTraverse(T);
}