Portal.
LCA。
询问树上两条路径是否有交点。
画图发现无非两种情况:
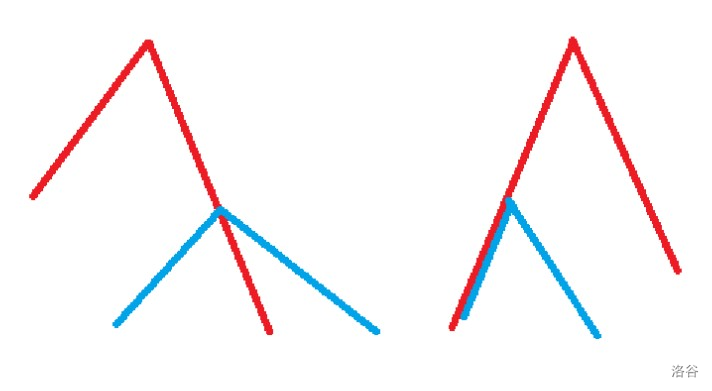
发现一条路径的起点和终点的 LCA 经过另一条路径,是两路径相交的充要条件。
考虑如何判断这个 LCA 在不在路径上。若 d ( s , LCA ) + d ( LCA , t ) = d ( s , t ) d(s,\text{LCA})+d(\text{LCA},t)=d(s,t) d(s,LCA)+d(LCA,t)=d(s,t),由于树上路径的唯一性,显然存在。
注意 LCA 函数,if(dep[f[x][i]]>=dep[y])
x
x
x 就可以往上跳。
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=1e5+5;
struct edge{int to,nxt;}e[maxn*2];
int head[maxn],cnt,dep[maxn],f[maxn][25];
void add(int x,int y){e[++cnt]={y,head[x]},head[x]=cnt;}
void dfs(int x,int fa)
{
dep[x]=dep[fa]+1,f[x][0]=fa;
for(int i=head[x];i;i=e[i].nxt)
{
if(e[i].to==fa) continue;
dfs(e[i].to,x);
}
}
int lca(int x,int y)
{
if(dep[x]<dep[y]) swap(x,y);
for(int i=20;i>=0;i--) if(dep[f[x][i]]>=dep[y]) x=f[x][i];
if(x==y) return x;
for(int i=20;i>=0;i--)
if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
return f[x][0];
}
int dis(int x,int y){return abs(dep[x]-dep[lca(x,y)])+abs(dep[y]-dep[lca(x,y)]);}
signed main()
{
int n,q;cin>>n>>q;
for(int i=1,u,v;i<n;i++) cin>>u>>v,add(u,v),add(v,u);
dfs(1,0);
for(int j=1;j<=20;j++) for(int i=1;i<=n;i++) f[i][j]=f[f[i][j-1]][j-1];
while(q--)
{
int a,b,c,d;cin>>a>>b>>c>>d;
int f1=lca(a,b),f2=lca(c,d);
if(dis(a,f2)+dis(b,f2)==dis(a,b)||dis(c,f1)+dis(d,f1)==dis(c,d)) cout<<"Y\n";
else cout<<"N\n";
// cout<<lca(a,b)<<endl;
}
return 0;
}