题目描述1
Problem - A - Codeforces

题目分析
样例1解释:
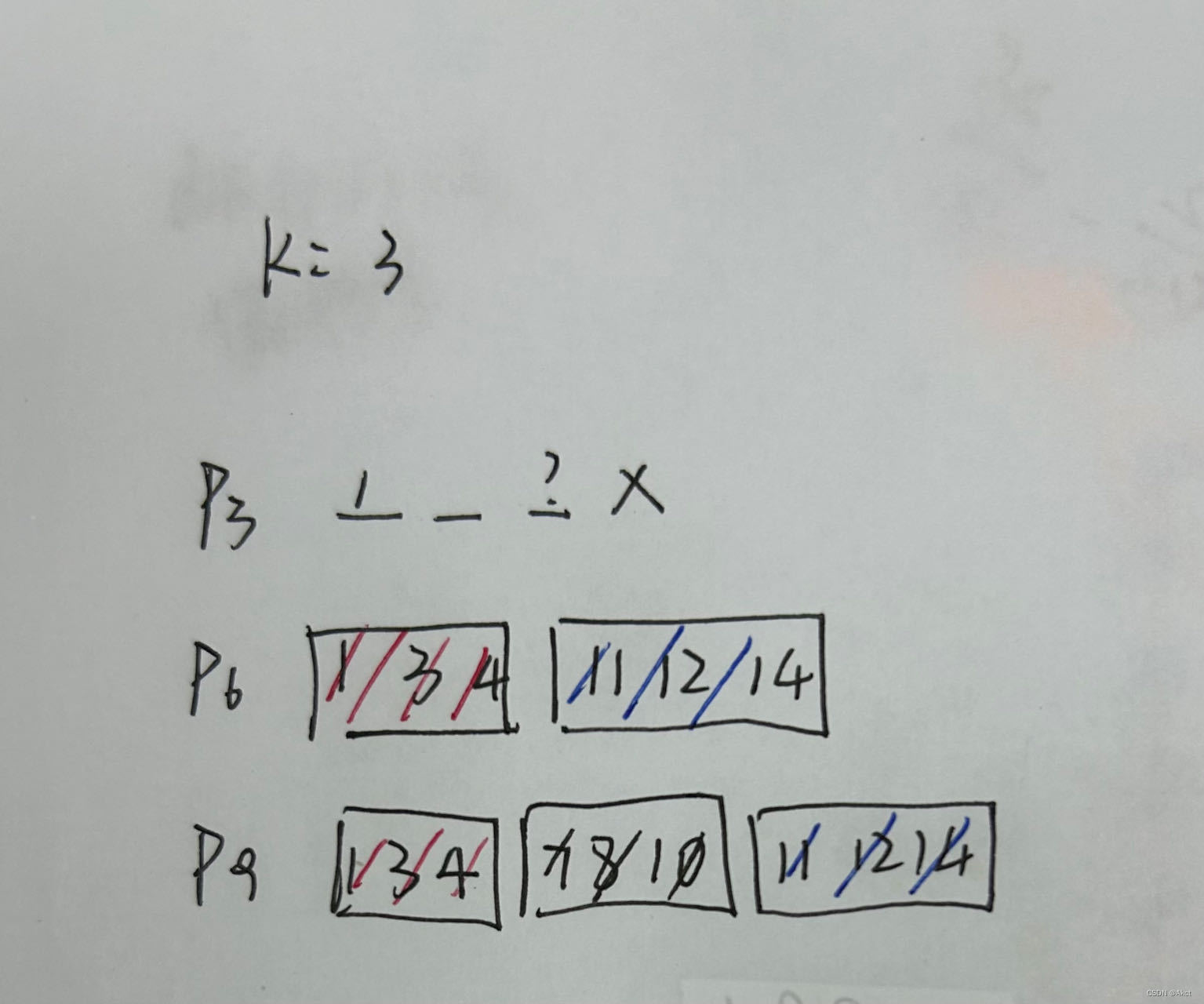
对于此题,我们采用贪心的想法,从1到n块数越少越好,故刚好符合最少的块数即可,由于第1块与第n块是我们必须要走的路,所以我们可以根据这两块砖的颜色进行分类判断。
如果这两块砖是一样的颜色,我们只需要判断这两块砖算上中间的颜色的总块数是否>=k即可。
如果这两块砖是不一样的颜色,我们需要分别从两端观察前面这部分的砖和后面这部分砖可以走的相同的颜色是否>=k即可
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
void solve()
{
int n, k, c[N];
cin >> n >> k;
for(int i = 1; i <= n; i ++)cin >> c[i];
if(c[1] == c[n])
{
int cnt = 0;
for(int i = 2; i <= n - 1; i ++)
{
if(c[i] == c[1])cnt ++;
}
if(cnt >= k - 2)cout << "YES" << '\n';
else cout << "NO" << '\n';
}
else
{
int l = n, r = 1,kl = 0, kr = 0;
for(int i = 1; i <= n && kl < k; i ++)
{
if(c[i] == c[1])
{
kl ++;
l = i;
}
}
for(int i = n; i >= 1 && kr < k; i --)
{
if(c[i] == c[n])
{
kr ++;
r = i;
}
}
if(kl == k && kr == k && l < r)cout << "YES" << '\n';
else cout << "NO" << '\n';
}
}
int main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t;
cin >> t;
while(t --)
{
solve();
}
return 0;
}题目描述2
Problem - B - Codeforces

题目样例示意:
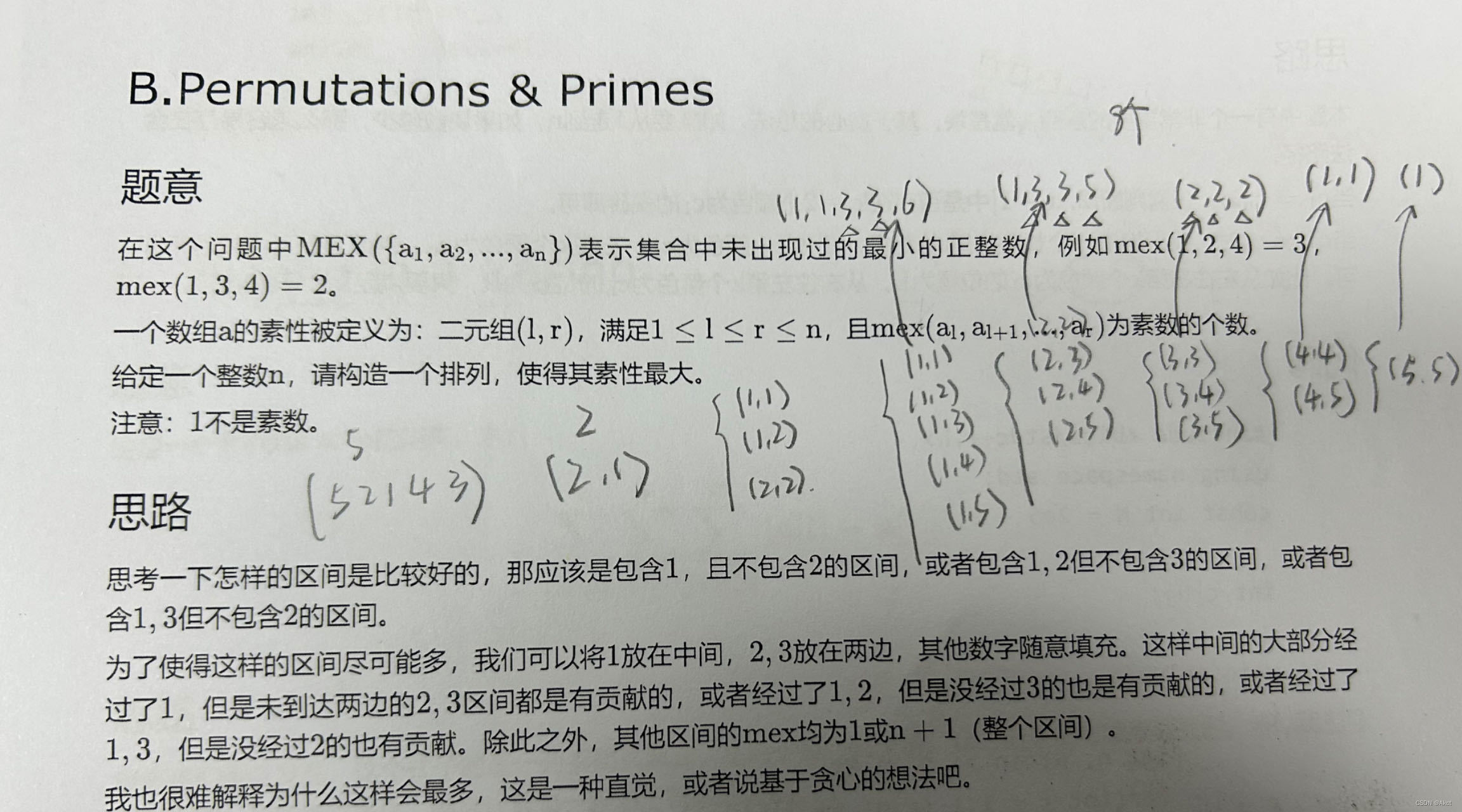
注意:找出的是排列也就是说数字不能重复,而且所有的数从小到大排序之后一定为连续的。
思考:什么是好区间?
包含1但是不包含2的区间(2)
包含1,2但是不包含3的区间(3)
包含1,3但是不包含2的区间(2)
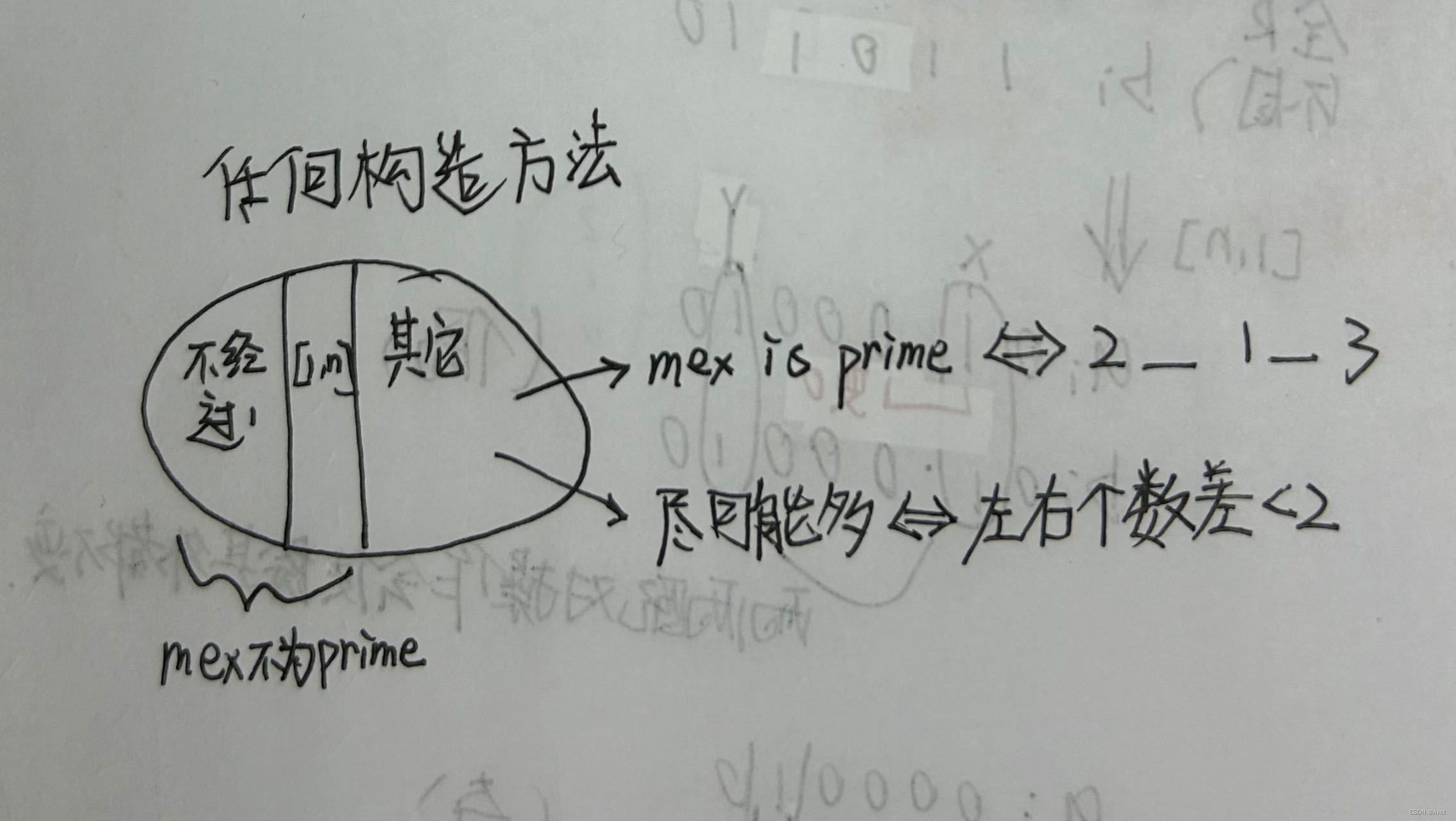
为了使这样的区间尽可能多
我们可以进行一个构造,题目要求在所有的区间中尽量使所有的素数结果最多我们可以将2和3放在两边,将1放在中间,这样中间的大部分经过了1,但是未到达两边的2,3区间都是有贡献的,或者经过了1,2,但是没经过3的也是有贡献的,或者经过了1,3但是没经过2的也有贡献。
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int a[N], n;
void solve()
{
cin >> n;
a[1] = 3, a[n] = 2;
int x = (n + 1) / 2;
a[x] = 1;
int k = 3;
for(int i = 2; i < x; i ++)
{
k ++;
a[i] = k;
}
for(int i = x + 1; i < n; i ++)
{
k ++;
a[i] = k;
}
for(int i = 1; i <= n; i ++)cout << a[i] << ' ';
cout << '\n';
}
int main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t;
cin >> t;
while(t --)
{
solve();
}
return 0;
}题目描述3
Problem - C - Codeforces
题目分析


此题我们需要掌握缩点的思想。
缩点:连续相同的字符变成一个字符即可
eg.00011110001011缩点成010101
需要不降序排列故左边0多好,"?"挨着哪个数就缩成哪个数,如果左右两边的数不一样就统一先按左边来缩数
#include<bits/stdc++.h>
using namespace std;
void solve()
{
string s ;
cin >> s;
int n = s.size() ;
for(int i = 0; i < n; i ++)
{
if(i != 0 && s[i] == '?')
{
s[i] = s[i - 1];
}
else if(i == 0 && s[i] == '?')s[i] = '0';
}
cout << s << '\n';
}
int main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t;
cin >> t;
while(t --)
{
solve();
}
return 0;
}题目描述4
Problem - D - Codeforces

题目分析

由上图可知变化一次必然会进行一次颜色的翻转
R表示数字不同的一列,B表示数字相同的一列
故要么是全R要么是全B才能到达一个全B的终点
一次操作到全R两次操作就会回到全B,故我们需要进行操作绑定
两两配对操作会使得除了这两个数之外的所有数都不发生变化(操作绑定)
但是如果剩下一个数没有配对时,可以进行如图右下角的方法计算
将需要改变的1存入vector中,并将其中的不能配对的奇数的1单独取出计算,剩下的进行配对即可
注:若取出的数的位置不在1时就可以改变(1, x - 1),(1, x)
若取出的数的位置在1时就可以改变(x, n)(x + 1, n)
#include<bits/stdc++.h>
using namespace std;
const int N = 3e5 + 10;
typedef pair<int, int> PII;
void solve()
{
char a[N], b[N];
int n;
vector<PII> ans;
vector<int> pos;
cin >> n;
cin >> a + 1 >> b + 1;
bool flag1 = 0, flag2 = 0;
for(int i = 1; i <= n; i ++)
{
if(a[i] == b[i])flag1 = 1;
else flag2 = 1;
}
if(flag1 && flag2)
{
cout << "NO" << '\n';
return;
}
if(flag2)//如果全是不相同的字符
{
ans.push_back({1, n});
for(int i = 1; i <= n; i ++)
{
if(a[i] == '0')a[i] = '1';
else a[i] = '0';
}
}
for(int i = 1; i <= n; i ++)
{
if(a[i] == '1')pos.push_back(i);
}
if(pos.size() & 1)
{
int x = pos.back();
if(x == 1)
{
ans.push_back({x, n});
ans.push_back({x + 1, n});
}
else
{
ans.push_back({1, x - 1});
ans.push_back({1, x});
}
pos.pop_back();
}
for(auto i : pos)ans.push_back({i, i});
cout << "YES" << '\n' << ans.size() << '\n';
for(auto i : ans)
{
cout << i.first << ' ' << i.second << '\n';
}
}
int main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t;
cin >> t;
while(t --)
{
solve();
}
return 0;
}题目描述5
Problem - E - Codeforces

题目分析

此题相当于找规律,从最大的数开始看起,第一个大于等于(n - 1)的平方数就是此处可以组成的平方数,发现会有连续的一段的平方数一样,判断限制条件,如果条件不满足就循环改数使其满足条件。
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int a[N];
void solve()
{
bitset<N> vis;
int n;
cin >> n;
int y = 0;
while(y * y < n - 1)y ++;
for(int i = n - 1; i >= 0; i --)
{
while(y * y - i >= n || vis[y * y - i])y --;
a[i] = y * y - i;
vis[a[i]] = true;
}
for(int i = 0; i < n; i ++)
{
cout << a[i] << ' ';
}
cout << '\n';
}
int main()
{
int t;
cin >> t;
while(t --)
{
solve();
}
return 0;
}