问题描述

如图1所示，设一个向量$\vec{v}$绕另一个向量$\vec{u}=[x,y,z{]}^T$旋转 θ 度，变换到${\vec{v}}^{{}^{\prime }}$。
求旋转后得到的向量${\vec{v}}^{{}^{\prime }}$的表示形式。

图1 三维向量旋转示意图

问题分析

由于转轴$\vec{u}$的模长$||\vec{u}||$对旋转结果没有影响，所以可以假设$||\vec{u}||=1$。
可以将$\vec{v}$分解为平行于旋转轴$\vec{u}$以及正交（垂直）于$\vec{u}$的两个分量，${\vec{v}}_{||}$和${\vec{v}}_{\perp }$，即$$\vec{v}={\vec{v}}_{||}+{\vec{v}}_{\perp }$$
可以分别旋转这两个分向量，再将它们旋转的结果相加获得旋转后的向量
$${\vec{v}}^{{}^{\prime }}={\vec{v}}_{||}^{{}^{\prime }}+{\vec{v}}_{\perp }^{{}^{\prime }}$$

图2 将 $\vec{v}$分解为平行于旋转轴 $\vec{u}$以及正交（垂直）于 $\vec{u}$的两个分量
可以看到， ${\vec{v}}_{||}$其实就是 $\vec{v}$ 在 $\vec{u}$上的正交投影，根据正交投影的公式，可以得出：
$${\vec{v}}_{||}=\frac{\vec{u}\cdot \vec{v}}{\vec{u}\cdot \vec{u}}\vec{u}=\frac{\vec{u}\cdot \vec{v}}{||\vec{u}|{|}^2}\vec{u}$$
根据 $||\vec{u}||=1$，可得： $${\vec{v}}_{||}=(\vec{u}\cdot \vec{v})\vec{u}$$
因为 $\vec{v}={\vec{v}}_{||}+{\vec{v}}_{\perp }$，所以： $${\vec{v}}_{\perp }=\vec{v}-{\vec{v}}_{||}=\vec{v}-(\vec{u}\cdot \vec{v})\vec{u}$$
分别求 ${\vec{v}}_{||}$和 ${\vec{v}}_{\perp }$的旋转结果就能得到 $\vec{v}$的旋转结果。

${\vec{v}}_{||}$的旋转

这种情况其实非常简单，从图2中就可以看到，${\vec{v}}_{||}$其实根本就没有被旋转，仍然与旋转轴$\vec{u}$重合，所以：
当 ${\vec{v}}_{||}$平行于旋转轴 $\vec{u}$时，旋转 θ 角度之后的${\vec{v}}_{||}^{{}^{\prime }}$为：${\vec{v}}_{||}^{{}^{\prime }}={\vec{v}}_{||}$

${\vec{v}}_{\perp }$的旋转

因为${\vec{v}}_{\perp }$与$\vec{u}$的是正交的，这个旋转可以看做是平面内的一个旋转。因为旋转不改变 ${\vec{v}}_{\perp }$的长度，所以旋转路径是一个圆。下面是这个旋转的示意图，右侧的为俯视图：

图3 $\vec{v}$绕轴 $\vec{u}$旋转的俯视图
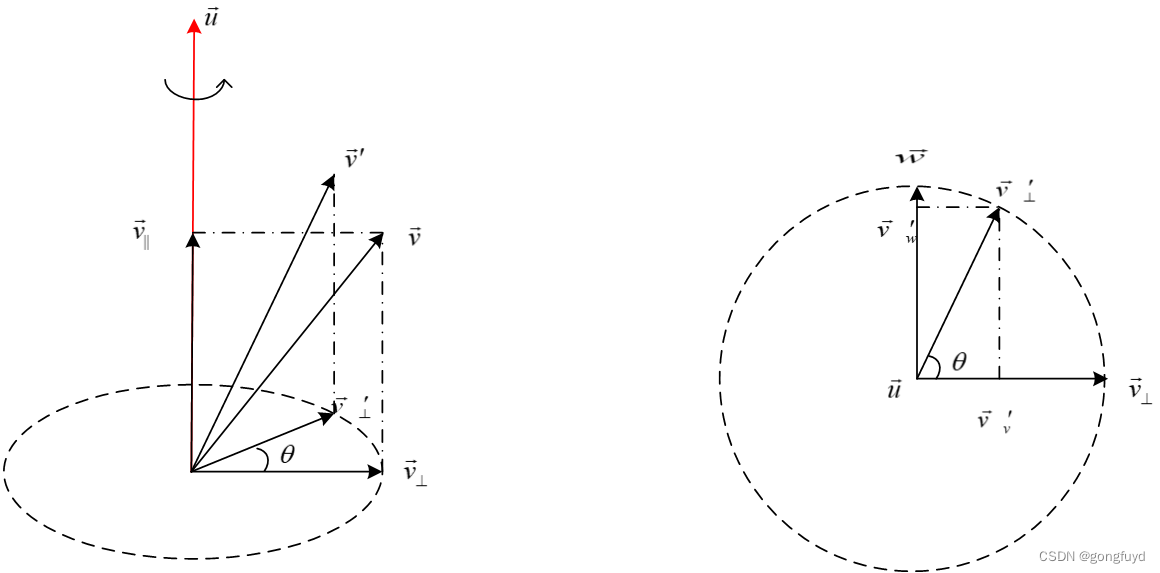
现在，3D 的旋转被转化为了 2D 平面上的旋转．由于在这个平面上们只有一个向量 ${\vec{v}}_{\perp }$，用它来表示一个旋转是不够的，还需要构造一个同时正交于 $\vec{u}$和 ${\vec{v}}_{\perp }$的向量 $\vec{w}$，这个可以通过叉乘来获得：
$$\vec{w}=\vec{u}\times {\vec{v}}_{\perp }$$
注意叉乘的顺序，因为使用的是右手坐标系统，按照右手定则可以发现这个新的向量 $\vec{w}$指向 ${\vec{v}}_{\perp }$逆时针旋转 𝜋/2 后的方向，并且和 ${\vec{v}}_{\perp }$一样也处于正交于 $\vec{u}$的平面内．因为 $||\vec{u}||=1$，可以发现 $$||\vec{w}||=||\vec{u}\times {\vec{v}}_{\perp }||=||\vec{u}||\cdot ||{\vec{v}}_{\perp }||\cdot sin(\pi /2)=||{\vec{v}}_{\perp }||$$
也就是说， $\vec{w}$和 ${\vec{v}}_{\perp }$的模长是相同的，所以， $\vec{w}$也位于圆上．有了这个新的向量 $\vec{w}$，就相当于在平面内有了两个坐标轴．我们现在可以把 ${\vec{v}}_{\perp }^{{}^{\prime }}$投影到 $\vec{w}$和 ${\vec{v}}_{\perp }$上，将其分解为 ${\vec{v}}_v^{{}^{\prime }}$和 ${\vec{v}}_w^{{}^{\prime }}$。使用三角学的知识就能得到： $${\vec{v}}_{\perp }^{{}^{\prime }}={\vec{v}}_v^{{}^{\prime }}+{\vec{v}}_w^{{}^{\prime }}=cos(\theta ){\vec{v}}_{\perp }+sin(\theta )\vec{w}=cos(\theta ){\vec{v}}_{\perp }+sin(\theta )(\vec{u}\times {\vec{v}}_{\perp })$$
这也就完成了旋转的第二步，可以得到这样一个定理：
当 ${\vec{v}}_{\perp }$正交于旋转轴 $\vec{u}$时，旋转 θ 角度之后的 ${\vec{v}}_{\perp }^{{}^{\prime }}$为： ${\vec{v}}_{\perp }^{{}^{\prime }}=cos(\theta ){\vec{v}}_{\perp }+sin(\theta )(\vec{u}\times {\vec{v}}_{\perp })$

$\vec{v}$的旋转

将上面的两个结果组合就可以获得$${\vec{v}}^{{}^{\prime }}={\vec{v}}_{||}^{{}^{\prime }}+{\vec{v}}_{\perp }^{{}^{\prime }}={\vec{v}}_{||}+cos(\theta ){\vec{v}}_{\perp }+sin(\theta )(\vec{u}\times {\vec{v}}_{\perp })$$
因为叉乘遵守分配律，
$$\vec{u}\times {\vec{v}}_{\perp }=\vec{u}\times (\vec{v}-{\vec{v}}_{\Vert |})=\vec{u}\times \vec{v}-\vec{u}\times {\vec{v}}_{\Vert |}=\vec{u}\times \vec{v}$$
最后，将${\vec{v}}_{||}=(\vec{u}\cdot \vec{v})\vec{u}$与${\vec{v}}_{\perp }=\vec{v}-(\vec{u}\cdot \vec{v})\vec{u}$代入$$\begin{gathered} {\vec{v}}^{{}^{\prime }}=(\vec{u}\cdot \vec{v})\vec{u}+cos(\theta )(\vec{v}-(\vec{u}\cdot \vec{v})\vec{u})+sin(\theta )(\vec{u}\times \vec{v}) \\ =cos(\theta )\vec{v}+(1-cos(\theta ))(\vec{u}\cdot \vec{v})\vec{u}+sin(\theta )(\vec{u}\times \vec{v}) \end{gathered}$$

结论

3D 向量旋转公式（向量型，一般情况，也叫做「Rodrigues’ Rotation Formula」）
3D 空间中任意一个向量$\vec{v}$沿着单位向量$\vec{u}$旋转 θ 角度之后得到的向量${\vec{v}}^{{}^{\prime }}$为：
$${\vec{v}}^{{}^{\prime }}=cos(\theta )\vec{v}+(1-cos(\theta ))(\vec{u}\cdot \vec{v})\vec{u}+sin(\theta )(\vec{u}\times \vec{v})$$

致谢

本文主要参考https://github.com/Krasjet/quaternion