Every day a Leetcode
题目来源:1122. 数组的相对排序
解法1:哈希
用集合 set 存储 arr2 中的元素。
遍历数组 arr1 ,设当前元素为 num:
- 如果 num 在 set 中出现,用哈希表 hash 记录 num 和它出现的次数。
- 否则,用将 num 插入数组 remain。
遍历数组 arr2,设当前元素为 num。向 ans 中插入 hash[num] 个 num。
将 remain 增序排序,将 remain 插入 ans 的后面。
代码:
/*
* @lc app=leetcode.cn id=1122 lang=cpp
*
* [1122] 数组的相对排序
*/
// @lc code=start
class Solution
{
public:
vector<int> relativeSortArray(vector<int> &arr1, vector<int> &arr2)
{
unordered_map<int, int> hash;
set<int> set(arr2.begin(), arr2.end());
vector<int> remain;
for (const int &num : arr1)
{
if (set.count(num))
hash[num]++;
else
remain.push_back(num);
}
vector<int> ans;
for (const int &num : arr2)
{
if (hash.count(num))
for (int i = 0; i < hash[num]; i++)
ans.push_back(num);
}
// 未在 arr2 中出现过的元素需要按照升序放在 arr1 的末尾
sort(remain.begin(), remain.end());
for (int i = 0; i < remain.size(); i++)
ans.push_back(remain[i]);
return ans;
}
};
// @lc code=end
结果:
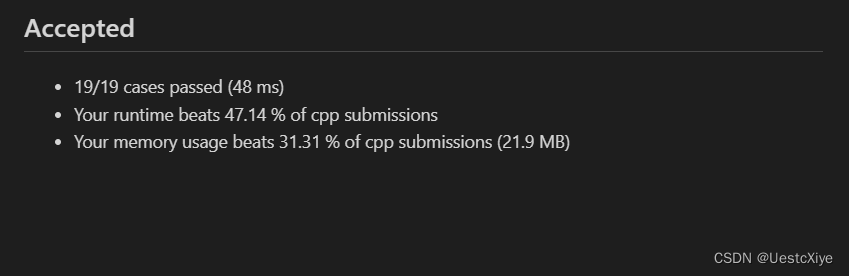
复杂度分析:
时间复杂度:O(mlogm+n),其中 m 和 n 分别是数组 arr1 和 arr2 的长度。构建哈希表的时间复杂度为 O(n),排序的时间复杂度为 O(mlogm)。
空间复杂度:O(logm+n),其中 m 和 n 分别是数组 arr1 和 arr2 的长度。哈希表的空间复杂度为 O(n),排序使用的栈的空间复杂度为 O(mlogm)。
解法2:计数排序
注意到本题中元素的范围为 [0, 1000],这个范围不是很大,我们也可以考虑不基于比较的排序,例如「计数排序」。
优化:实际上,我们不需要使用长度为 1001 的数组,而是可以找出数组 arr1 中的最大值 upper,使用长度为 upper+1 的数组即可。
代码:
/*
* @lc app=leetcode.cn id=1122 lang=cpp
*
* [1122] 数组的相对排序
*/
// @lc code=start
// class Solution
// {
// public:
// vector<int> relativeSortArray(vector<int> &arr1, vector<int> &arr2)
// {
// unordered_map<int, int> hash;
// set<int> set(arr2.begin(), arr2.end());
// vector<int> remain;
// for (const int &num : arr1)
// {
// if (set.count(num))
// hash[num]++;
// else
// remain.push_back(num);
// }
// vector<int> ans;
// for (const int &num : arr2)
// {
// if (hash.count(num))
// for (int i = 0; i < hash[num]; i++)
// ans.push_back(num);
// }
// // 未在 arr2 中出现过的元素需要按照升序放在 arr1 的末尾
// sort(remain.begin(), remain.end());
// for (int i = 0; i < remain.size(); i++)
// ans.push_back(remain[i]);
// return ans;
// }
// };
class Solution
{
public:
vector<int> relativeSortArray(vector<int> &arr1, vector<int> &arr2)
{
int upper = *max_element(arr1.begin(), arr1.end());
vector<int> freq(upper + 1, 0);
for (const int &num : arr1)
freq[num]++;
vector<int> ans;
for (const int &num : arr2)
{
for (int i = 0; i < freq[num]; i++)
ans.push_back(num);
freq[num] = 0;
}
for (int num = 0; num <= upper; num++)
for (int i = 0; i < freq[num]; i++)
ans.push_back(num);
return ans;
}
};
// @lc code=end
结果:
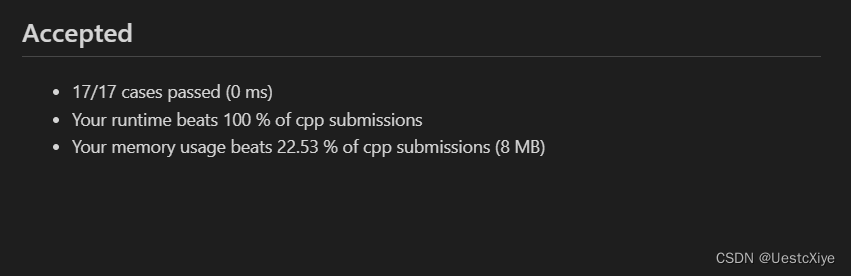
复杂度分析:
时间复杂度:O(m+n+upper),其中 m 和 n 分别是数组 arr1 和 arr2 的长度。upper 是数组 arr1 的最大值。
空间复杂度:O(upper),其中 upper 是数组 arr1 的最大值。即为数组 freq 需要使用的空间。