【高阶数据结构】搜索二叉树

news2024/11/24 0:08:34

🌈欢迎来到数据结构专栏~~搜索二叉树

  • (꒪ꇴ꒪(꒪ꇴ꒪ )🐣,我是Scort
  • 目前状态：大三非科班啃C++中
  • 🌍博客主页：张小姐的猫~江湖背景
  • 快上车🚘，握好方向盘跟我有一起打天下嘞！
  • 送给自己的一句鸡汤🤔：
  • 🔥真正的大师永远怀着一颗学徒的心
  • 作者水平很有限，如果发现错误，可在评论区指正，感谢🙏
  • 🎉🎉欢迎持续关注！
    请添加图片描述

请添加图片描述

二叉搜索树

  • 🌈欢迎来到数据结构专栏~~搜索二叉树
    • 一. 概念
    • 二. 基本操作
      • 🌈查找元素 Search
      • 🌈插入 Insert
      • 🌈删除 Delete
    • 三. 进阶操作 ~ 递归写法
      • 🥑递归查找 Search
      • 🥑递归插入 Insert
      • 🥑递归删除 Delete
    • 四. 性能分析
    • 五. 二叉搜索树的应用
      • 💦Key模型
      • 💦Key- Value模型
    • 附源码
      • `BinarySearchTree.h`
      • `test.c`
  • 📢写在最后

请添加图片描述

一. 概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

  • 若它的左子树不为空，则 左子树上所有节点的值都小于根节点的值

  • 若它的左子树不为空，则 右子树上所有节点的值都大于根节点的值

  • 它的左右子树也分别为二叉搜索树

在这里插入图片描述

二. 基本操作

🌈查找元素 Search

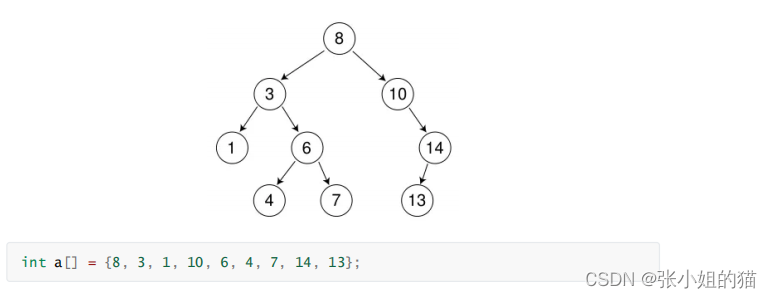
在这里插入图片描述

  • 从根开始比较，查找，比根大则往右边走查找，比根小则往左边走查找
  • 最多查找高度次，走到到空，还没找到，这个值不存在
	//查找
	bool Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)
			{
				cur = cur->_right;
			}
			else if (cur->_key < key)
			{
				cur = cur->_left;
			}
			else
			{
				return true;
			}
		}
	}

🌈插入 Insert

思路如下：

  1. 树为空，则直接新增节点，直接插入root指针即可
  2. 因为不能插入重复的元素，并且每次插入都是要定位到空节点的位置；定义一个 cur 从root开始，插入的元素比当前位置元素小就往左走，比当前位置元素大就往右走，直到为空；
  3. 再定义一个parent记录 cur的前一个位置，最后判断cur是parent的左子树or右子树

动画演示：

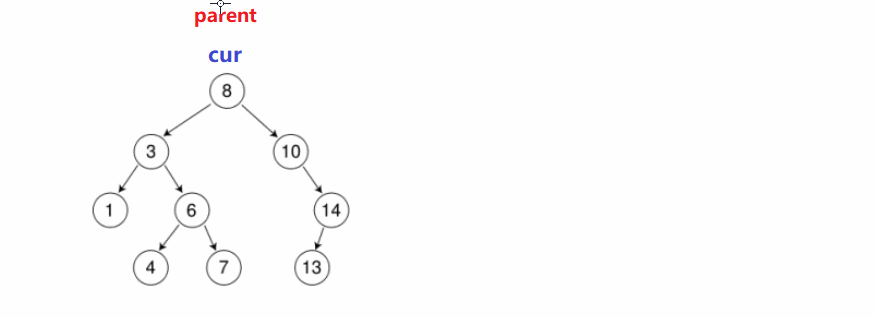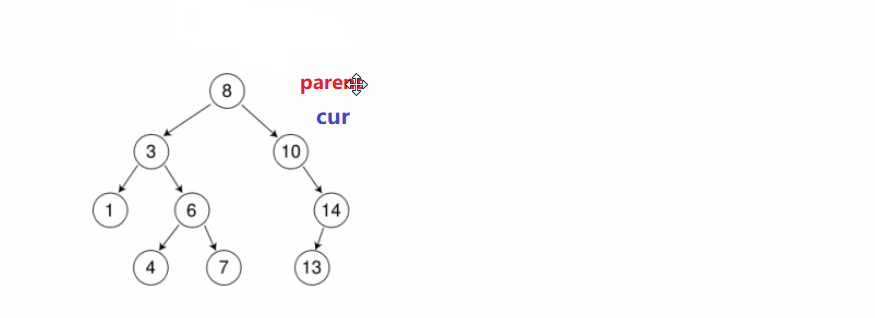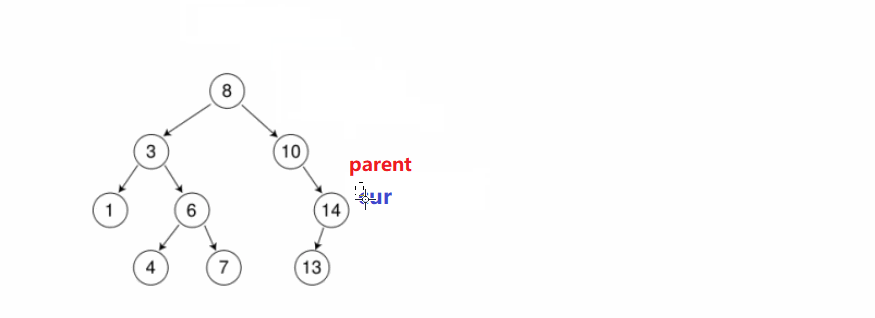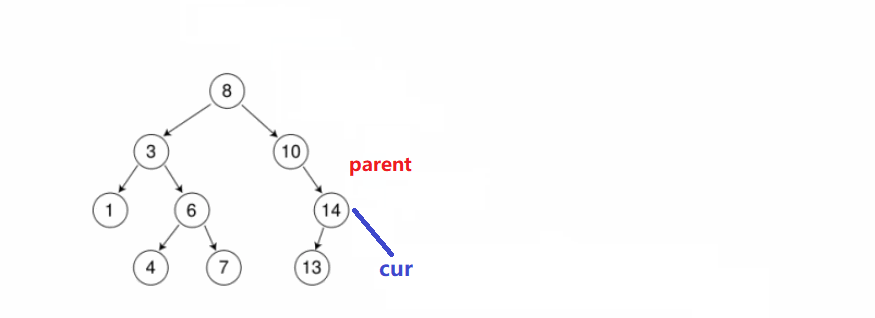
请添加图片描述

    //相同的
	bool Insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)
			{ 
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

		//链接节点
		cur = new Node(key);
		if(parent->_key < key)
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}

		return true;
	}

🌈删除 Delete

删除有三种情况：

  1. 无牵无挂型：如果是叶子结点，直接置空并链接到空指针
  2. 独生子女型：只有一个子节点，删除自己本身，并链接子节点和父节点
  3. 替罪羊型：寻找出右子树最小节点、左子树最大节点，其节点可以作为交换节点和删除结点进行交换，交换后删除交换节点、交换节点要么没有孩子，要么只有一个孩子可以直接删除

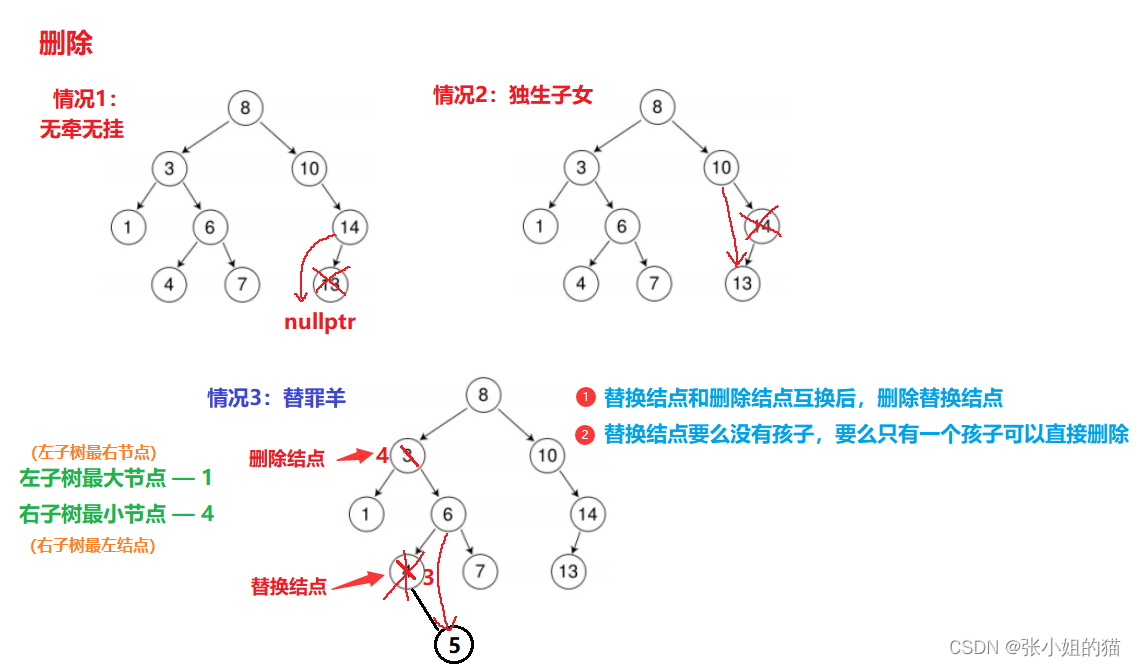
在这里插入图片描述

其实在代码层面第一种情况可以归类到第二种情况（没有左孩子，就链接上右孩子）

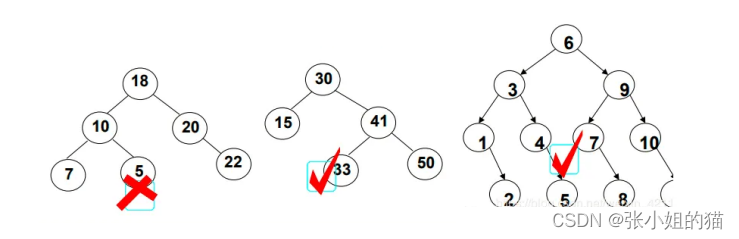
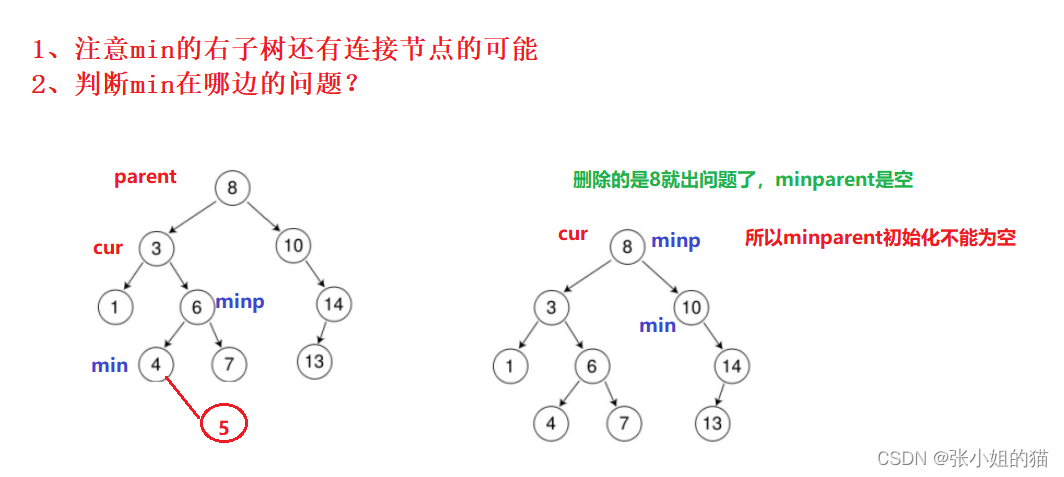
在代码层面实际上是四种：

  1. 左为空
  2. 右为空
  3. 左右都为空（细节很多看下图）
  4. cur是跟节点位置（特殊情况移动root）

在这里插入图片描述

	//删除
	bool Erase(const K& key)
	{
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				//找到了，开始删除，有三种情况
				//1、左为空
				//2、右为空
				//3、左右都不为空
				//4、删除跟root 要移动root（特殊情况）
				if (cur->_left == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_right;
					}
					else
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_right;
						}
						else
						{
							parent->_right = cur->_right;
						}
					}
					delete cur;
					cur = nullptr;
				}
				else if (cur->_right == nullptr)
				{
					if (_root == cur)
					{
						_root = cur->_left;
					}
					else
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_left;
						}
						else
						{
							parent->_right = cur->_left;
						}
					}
					delete cur;
					cur = nullptr;
				}
				else
				{
					//左右都不为空  ——  替换法删除
					//找到右树最小节点进行替换
					Node* min = cur->_right;
					Node* minparent = nullptr;
					while (min->_left)
					{
						minparent = min;
						min = min->_left;
					}
					swap(cur->_key, min->_key);

					//注意min的右子树还有连接节点的可能
					//和判断min在哪边的问题？
					if (minparent->left = min)
					{
						minparent->_left = min->_right;
					}
					else
					{
						minparent->_right = min->_right;
					}
					delete min;
				}
				return true;
			}
		}
		return false;
	}

三. 进阶操作 ~ 递归写法

🥑递归查找 Search

唤起递归的记忆吧

	void _FindR(Node* root, const K& key)
	{
		//根为空的情况下
		if (root == nullptr)
		{
			return false;
		}

		if (root->_key < key)
		{
			return _FindR(root->_right);
		}
		else if (root->_key > key)
		{
			return _FindR(root->_left);
		}
		else
		{
			return true;
		}
	}

🥑递归插入 Insert

要注意，这里有“神之一手”

在这里插入图片描述

在这里插入图片描述

	void _InsertR(Node*& root, const K& key)
	{
		if (root == nullptr)
		{
			root = new Node(key);
			return true;
		}

		if (root->_key < key)
		{
			return _InsertR(root->_right, key);
		}
		else if (root->_key > key)
		{
			return _InsertR(root->_left, key);
		}
		else
		{
			return false;
		}
	}

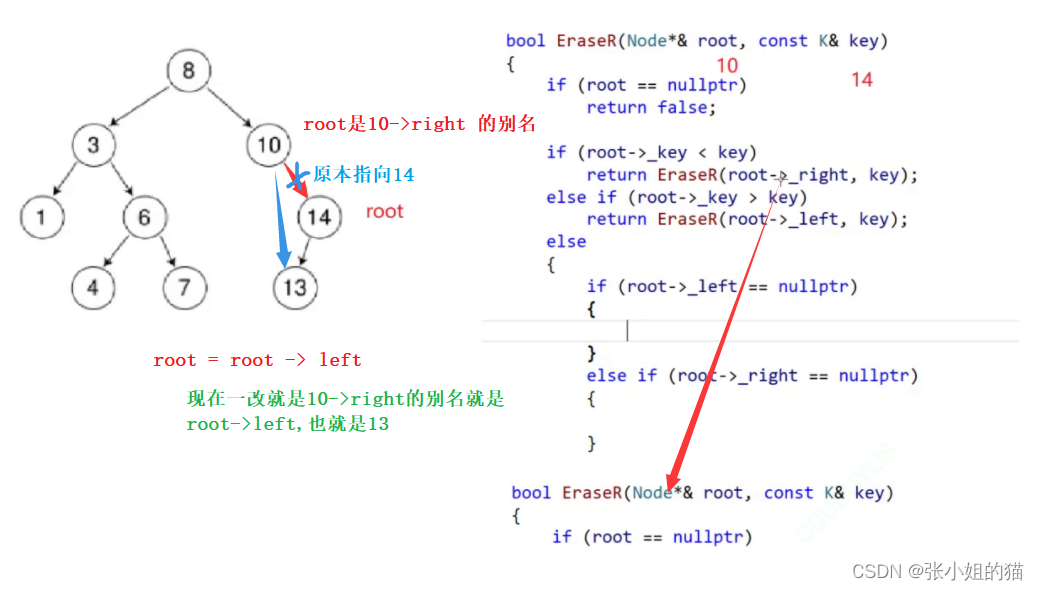
🥑递归删除 Delete

神之操作：root = root->_left

在这里插入图片描述

在这里插入图片描述

	bool _EraseR(Node*& root, const K& key)
	{
		if (root == nullptr)
		{
			return false;
		}

		if (root->_key < key)
		{
			return _EraseR(root->_right, key);
		}
		else if (root->_key > key)
		{
			return _EraseR(root->_left, key);
		}
		else 
		{
			//找到了要删除的位置
			Node* del = root;
			if (root->_left == nullptr)
			{
				root = root->_right;
			}
			else if (root->_right == nullptr)
			{
				root = root->_left;
			}
			else
			{
				//找右树的最小节点 - 替换删除
				Node* min = root->_right;
				while (min->_left)
				{
					min = min->_left;
				}
				swap(min->_key, root->_key);
				return _Erase(root->_right)
			}

			delete del;
			return true;
		}
	}

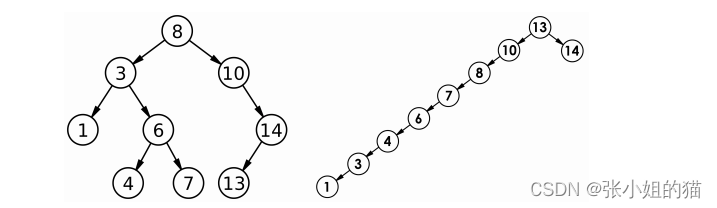
四. 性能分析

最优情况下，二叉搜索树为完全二叉树(或者接近完全二叉树)，其平均比较次数为： l o g 2 N log_2 N log2​N
最差情况下，二叉搜索树退化为单支树(或者类似单支)，其平均比较次数为： N 2 \frac{N}{2} 2N​

在这里插入图片描述

五. 二叉搜索树的应用

💦Key模型

key的搜索模型，判断关键字在不在

  • 刷卡进宿舍楼
  • 检测一篇英文文档中单词拼写是否正确

以上都是把全部相关的资料都插入到一颗搜索树中，然后开始寻找，判断在不在

💦Key- Value模型

KV模型：每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。

  • 比如英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英文单词与其对应的中文<word, chinese>就构成一种键值对
  • 再比如统计单词次数，统计成功后，给定单词就可快速找到其出现的次数，单词与其出现次数就是<word, count>就构成一种键值对
// 改造二叉搜索树为KV结构
template<class K, class V>
struct BSTNode
{
	BSTNode(const K& key = K(), const V& value = V())
		: _pLeft(nullptr), _pRight(nullptr), _key(key), _Value(value)
	{}
	BSTNode<T>* _pLeft;
	BSTNode<T>* _pRight;
	K _key;
	V _value
};
template<class K, class V>
class BSTree
{
	typedef BSTNode<K, V> Node;
	typedef Node* PNode;
public:
	BSTree() : _pRoot(nullptr) {}
	PNode Find(const K& key);
	bool Insert(const K& key, const V& value)
		bool Erase(const K& key)
private:
	PNode _pRoot;
}

void TestBSTree3()
{
	// 输入单词，查找单词对应的中文翻译
	BSTree<string, string> dict;
	dict.Insert("string", "字符串");
	dict.Insert("tree", "树");
	dict.Insert("left", "左边、剩余");
	dict.Insert("right", "右边");
	dict.Insert("sort", "排序");
	// 插入词库中所有单词
	string str;
	while (cin >> str)
	{
		BSTreeNode<string, string>* ret = dict.Find(str);
		if (ret == nullptr)
		{
			cout << "单词拼写错误，词库中没有这个单词:" << str << endl;
		}
		else
		{
			cout << str << "中文翻译:" << ret->_value << endl;
		}
	}
}

附源码

BinarySearchTree.h

#pragma once

#include<iostream>
using namespace std;


namespace Key
{
	template<class K>
	struct BSTreeNode
	{
		BSTreeNode<K>* _left;
		BSTreeNode<K>* _right;
		K _key;

		BSTreeNode(const K& key)
			:_left(nullptr)
			, _right(nullptr)
			, _key(key)
		{}
	};

	//class BinarySearchTree
	template<class K>
	class BSTree
	{
		typedef BSTreeNode<K> Node;

	public:
		//插入
		bool Insert(const K& key)
		{
			if (_root == nullptr)
			{
				_root = new Node(key);
				return true;
			}

			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return false;
				}
			}

			//链接节点
			cur = new Node(key);
			if (parent->_key < key)
			{
				parent->_right = cur;
			}
			else
			{
				parent->_left = cur;
			}

			return true;
		}

		//查找
		bool Find(const K& key)
		{
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key > key)
				{
					cur = cur->_right;
				}
				else if (cur->_key < key)
				{
					cur = cur->_left;
				}
				else
				{
					return true;
				}
			}
		}

		//删除
		bool Erase(const K& key)
		{
			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					//找到了，开始删除，有三种情况
					//1、左为空
					//2、右为空
					//3、左右都不为空
					//4、删除跟root 要移动root（特殊情况）
					if (cur->_left == nullptr)
					{
						if (cur == _root)
						{
							_root = cur->_right;
						}
						else
						{
							if (cur == parent->_left)
							{
								parent->_left = cur->_right;
							}
							else
							{
								parent->_right = cur->_right;
							}
						}
						delete cur;
						cur = nullptr;
					}
					else if (cur->_right == nullptr)
					{
						if (_root == cur)
						{
							_root = cur->_left;
						}
						else
						{
							if (cur == parent->_left)
							{
								parent->_left = cur->_left;
							}
							else
							{
								parent->_right = cur->_left;
							}
						}
						delete cur;
						cur = nullptr;
					}
					else
					{
						//左右都不为空  ——  替换法删除
						//找到右树最小节点进行替换
						Node* min = cur->_right;
						Node* minparent = nullptr;
						while (min->_left)
						{
							minparent = min;
							min = min->_left;
						}
						swap(cur->_key, min->_key);

						//注意min的右子树还有连接节点的可能
						//和判断min在哪边的问题？
						if (minparent->_left = min)
						{
							minparent->_left = min->_right;
						}
						else
						{
							minparent->_right = min->_right;
						}
						delete min;
					}
					return true;
				}
			}
			return false;
		}


		//这样就能避免this指针问题,因为递归必须显示给参数
		void InOrder()
		{
			_InOrder(_root);//这样就可以使用_root
			cout << endl;
		}


		/// //
		/// 递归写法

		bool FindR(const K& key)
		{
			return _FindR(_root, key);
		}

		bool InsertR(const K& key)
		{
			return _InsertR(_root, key);
		}

		bool EraseR(const K& key)
		{
			return _EraseR(_root, key);
		}

		~BSTree()
		{
			_Destory(_root);
		}

		//BSTree()
		//{}

		//C++11的用法：强制编译器生成默认构造
		BSTree() = default;


		//拷贝构造
		BSTree(const BSTree<K>& t)
		{
			_root = _Copy(t._root);
		}

		//t2 = t1
		BSTree<K>& operator = (BSTree<K> t)
		{
			swap(_root, t._root);
			return *this;
		}

	private:
		Node* _Copy(Node* root)
		{
			if (root == nullptr)
			{
				return nullptr;
			}

			Node* copyRoot = new Node(root->_key);
			copyRoot->_left = _Copy(root->_left);
			copyRoot->_right = _Copy(root->_right);
			return copyRoot;
		}

		void _Destory(Node*& root)
		{
			if (root == nullptr)
			{
				return;
			}

			_Destory(root->_left);
			_Destory(root->_right);
			delete root;
			root = nullptr;
		}

		bool _EraseR(Node*& root, const K& key)
		{
			if (root == nullptr)
			{
				return false;
			}

			if (root->_key < key)
			{
				return _EraseR(root->_right, key);
			}
			else if (root->_key > key)
			{
				return _EraseR(root->_left, key);
			}
			else
			{
				//找到了要删除的位置
				Node* del = root;
				if (root->_left == nullptr)
				{
					root = root->_right;
				}
				else if (root->_right == nullptr)
				{
					root = root->_left;
				}
				else
				{
					//找右树的最小节点 - 替换删除
					Node* min = root->_right;
					while (min->_left)
					{
						min = min->_left;
					}
					swap(min->_key, root->_key);
					return _Erase(root->_right);//防止找不到key的情况
				}

				delete del;
				return true;
			}
		}

		void _InsertR(Node*& root, const K& key)
		{
			if (root == nullptr)
			{
				root = new Node(key);
				return true;
			}

			if (root->_key < key)
			{
				return _InsertR(root->_right, key);
			}
			else if (root->_key > key)
			{
				return _InsertR(root->_left, key);
			}
			else
			{
				return false;
			}
		}

		void _FindR(Node* root, const K& key)
		{
			//根为空的情况下
			if (root == nullptr)
			{
				return false;
			}

			if (root->_key < key)
			{
				return _FindR(root->_right, key);
			}
			else if (root->_key > key)
			{
				return _FindR(root->_left, key);
			}
			else
			{
				return true;
			}
		}

		void _InOrder(Node* root)
		{
			if (root == nullptr)
			{
				return;
			}

			_InOrder(root->_left);
			cout << root->_key << " ";
			_InOrder(root->_right);
		}

	private:
		Node* _root = nullptr;
	};

	void TestBSTree1()
	{
		BSTree<int> t;
		int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
		for (auto e : a)
		{
			t.Insert(e);
		}

		//排序+去重
		t.InOrder();

		t.Erase(3);
		t.InOrder();

		t.Erase(6);
		t.InOrder();
	}


	void TestBSTree2()
	{
		BSTree<int> t;
		int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
		for (auto e : a)
		{
			t.Insert(e);
		}

		BSTree<int> copy = t;
		copy.InOrder();
		t.InOrder();
	}
}

test.c

#include "BinarySearchTree.h"

int main()
{
	//TestBSTree1();
	/*TestBSTree2();*/
	TestBSTree3();

	return 0;
}

📢写在最后

多多更新

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/116801.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Word控件Spire.Doc 【评论】教程(2)：在 C#、VB.NET 中删除和替换 Word 文档中的注释

Word控件Spire.Doc 【评论】教程(2)：在 C#、VB.NET 中删除和替换 Word 文档中的注释

Spire.Doc for .NET是一款专门对 Word 文档进行操作的 .NET 类库。在于帮助开发人员无需安装 Microsoft Word情况下&#xff0c;轻松快捷高效地创建、编辑、转换和打印 Microsoft Word 文档。拥有近10年专业开发经验Spire系列办公文档开发工具&#xff0c;专注于创建、编辑、转…
阅读更多...
130页5万字某市档案馆数字档案馆建设方案

130页5万字某市档案馆数字档案馆建设方案

【版权声明】本资料来源网络&#xff0c;仅用于行业知识分享&#xff0c;供个人学习参考&#xff0c;请勿商用。【侵删致歉】如有侵权请联系小编&#xff0c;将在收到信息后第一时间进行删除&#xff01; 完整资料领取见文末&#xff0c;部分资料内容&#xff1a; 国家档案局证…
阅读更多...
MySQL主从搭建

MySQL主从搭建

MySQL主从搭建一 主从配置原理二 搭建步骤&#xff08;基于两个docker容器&#xff09;三 django实现读写分离3.1 配置数据库3.2 models中创建表3.3 数据库迁移3.4 指定要使用的数据库四 Pycharm远程连接服务器进行代码的运行与调试五 Pycharm远程链接docker开发5.1 操作 docke…
阅读更多...
SSM图书管理系统（增强版，附源码）

SSM图书管理系统（增强版，附源码）

前篇引入&#xff08;新人必看&#xff09;&#xff1a;SSM图书管理系统&#xff08;原版&#xff09; 之前给大家分享过SSM图书管理系统项目的源码&#xff0c;热度较高&#xff0c;但我也发现功能并不是很全面&#xff0c;所以这次对系统进行了功能增强&#xff0c;以下是系…
阅读更多...
新手入门搭建一个spring boot项目

新手入门搭建一个spring boot项目

1. 打开Idea,新建一个maven项目&#xff0c;详细情况见下图&#xff0c;&#xff08;idea版本2021.1.2&#xff09; 2.查看新建项目的maven包是否存在&#xff0c; 注意&#xff1a;maven包需要自己去下载&#xff0c;注意要下载与版本对应匹配的包 3.导入spring boot 相关的依…
阅读更多...
springboot 连接不上 redis 的三种解决方案！

springboot 连接不上 redis 的三种解决方案！

针对于springboot 连接不上 redis 这种情况&#xff0c;首先&#xff0c;我们最简单直接的方法就是需要确认Redis是否已经正常启动&#xff08;验证方法&#xff1a;如果安装在Linux下的话可以使用ps-ef|grep redis来进行确认是否开启&#xff09; 如果未开启&#xff0c;我们可…
阅读更多...
STL-string的接口使用及模拟实现

STL-string的接口使用及模拟实现

文章目录string类的介绍string类的常用接口介绍 构造相关 无参构造字符串构造拷贝构造 容量相关的接口 sizereserveresizecapacityemptyclear 数据访问及遍历相关的接口 operator[]begin endrbegin rend 修改数据相关的接口 push_backoperatorinserterasec_strfind npossubs…
阅读更多...
Redis搭建主从集群

Redis搭建主从集群

搭建集群 建集群的第一件事情我们需要一些运行在 集群模式的Redis实例。这意味这集群并不是由一些普通的Redis实例组成的&#xff0c;集群模式需要通过配置启用&#xff0c;开启集群模式后的Redis实例便可以使用集群特有的命令和特性了。 下面是一个最少选项的集群的配置文件…
阅读更多...
@Builder注解在子类中使用遇到的问题

@Builder注解在子类中使用遇到的问题

场景 在项目开发中&#xff0c;需要基于某个类进行一些字段的拓展&#xff0c;那么自然而然想到的做法是extends该类。而两个类都需要使用Builder进行构造。代码如下&#xff1a; Data Builder AllArgsConstructor NoArgsConstructor public class EmployeeDto {private Stri…
阅读更多...
详解 Vue3 中如何使用 Proxy 来实现响应式的技术~

详解 Vue3 中如何使用 Proxy 来实现响应式的技术~

详解 Vue3 中如何使用 Proxy 来实现响应式的技术~写在前面剖析 Vue2 中是如何实现响应式的Vue2 的响应式存在什么问题&#xff1f;Vue3 响应式一、ref 函数二、reactive 函数reactive 响应式原理 - ProxyVue3 中的响应式解决了 Vue2 中存在的问题写在前面 Vue3 中的响应式原理…
阅读更多...
C++：STL：常见容器：stack，queue, list

C++：STL：常见容器：stack，queue, list

一&#xff1a;stack容器 1.1: stack基本概念 概念&#xff1a;stack是一种先进后出 &#xff08;First in last out FILO&#xff09;的数据结构&#xff0c;它只有一个出口。 栈中&#xff1a; 1&#xff1a;只有栈顶的元素才可以被外界使用&#xff0c;因此栈不允许有遍历…
阅读更多...
从FrameDebugger看Unity渲染

从FrameDebugger看Unity渲染

从FrameDebugger看Unity渲染(一) Unity如何渲染一个3D2D的游戏画面&#xff0c;今天通过FrameDebugger来看下Unity内置渲染管线的渲染策略, 后续再出一些URP渲染管线相关的文章。 对啦&#xff01;这里有个游戏开发交流小组里面聚集了一帮热爱学习游戏的零基础小白&#xff0c…
阅读更多...
MyBatis 实现复杂 Sql 查询

MyBatis 实现复杂 Sql 查询

resultMap 结果映射 resultMap 元素是 MyBatis 中最重要最强大的元素&#xff0c;之前所写的 sql 语句&#xff0c;返回值都是简单的基本数据类型或者某一个实体类&#xff0c;比如下面这段 sql 返回的就是最简单的 User 类型。 <select id"getUserById" result…
阅读更多...
微信HOOK 协议接口 实战开发篇 3.收发文本消息 附详细步骤

微信HOOK 协议接口 实战开发篇 3.收发文本消息 附详细步骤

前言&#xff1a;本次文章附带详细的HOOK步骤&#xff0c;感兴趣可以尝试一番 使用了之前文章提到的字符搜索法 接收消息 1.OD打开微信&#xff0c;点击e&#xff0c;进入模块列表 2.双击wechatwin模块进入汇编代码页面 3.右键菜单&#xff0c;选择如图示选项 4.进入字符页…
阅读更多...
【 uniapp - 黑马优购 | tabBar】如何创建和配置标签栏

【 uniapp - 黑马优购 | tabBar】如何创建和配置标签栏

个人名片&#xff1a; &#x1f43c;作者简介&#xff1a;一名大二在校生&#xff0c;讨厌编程&#x1f38b; &#x1f43b;‍❄️个人主页&#x1f947;&#xff1a;小新爱学习. &#x1f43c;个人WeChat&#xff1a;hmmwx53 &#x1f54a;️系列专栏&#xff1a;&#x1f5bc…
阅读更多...
zabbix监控redis修正nodata问题

zabbix监控redis修正nodata问题

之前根据网上的资料尝试监控redis&#xff0c;完成后编写了文档。 https://blog.csdn.net/bigwood99/article/details/128404063 这几天观察数据&#xff0c;发现没有数据被采集。 在图标中显示no data。 检查模板中item和graphs设置&#xff0c;发现key中没有使用引号。 …
阅读更多...
修复U盘【笔记】

修复U盘【笔记】

修复U盘【笔记】前言参考修复U盘问题0.芯片精灵查看1.用APTool软件擦除量产信息2.用CBMTool量产U盘结果我的版本最后前言 以下内容源自网络 仅供学习交流使用 参考 总体步骤&芯片精灵下载&#xff1a;https://www.xpwin7.com/jiaocheng/25627.html 资源下载网址来源&am…
阅读更多...
组织上线 | 资源共享，协作自如

组织上线 | 资源共享，协作自如

新功能&#xff5e;&#xff01;期待已久的组织协作上线啦&#xff01; 上线后支持在组织下创建镜像&#xff0c;组织成员可查看、拉取镜像&#xff0c;快速实现镜像资源共享&#xff0c;组织高效协同。 具体怎么操作呢&#xff1f;跟我一起来看一下吧&#xff5e; 创建组织 …
阅读更多...
Pandas计算历史均值

Pandas计算历史均值

在用Python进行时间序列分析时&#xff0c;我们可能经常需要计算历史的一些特征。一般会使用rolling()函数&#xff0c;这里介绍一下计算包括当前行的历史特征和不包括当前行的历史特征 1. 包括当前行 这里先简单介绍一下rolling()函数 pandas.DataFrame.rolling官方文档 Dat…
阅读更多...
数据库，计算机网络、操作系统刷题笔记19

数据库，计算机网络、操作系统刷题笔记19

数据库&#xff0c;计算机网络、操作系统刷题笔记19 2022找工作是学历、能力和运气的超强结合体&#xff0c;遇到寒冬&#xff0c;大厂不招人&#xff0c;可能很多算法学生都得去找开发&#xff0c;测开 测开的话&#xff0c;你就得学数据库&#xff0c;sql&#xff0c;oracle…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023