GDPU 数据结构天码行空8

news2024/11/25 18:42:23

实验八二叉树的建立及遍历应用

一、【实验目的】

1、掌握二叉树的建立方法
2、掌握二叉树遍历的基本方法（前序、中序、后序）
3、掌握递归二叉树遍历算法的应用

二、【实验内容】

1.构造一棵二叉树,树的形态如下图(亦见附件)所示，打印出先序遍历、中序遍历、后序遍历的遍历序列。
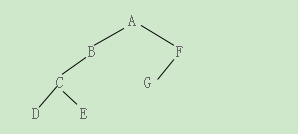
在这里插入图片描述

2.选择一种遍历方式计算该树中叶子结点的个数，并打印出叶子结点。
3.编写一个层序遍历算法，利用队列结构按层次（同一层自左至右）输出二叉树中所有的结点。

三、【实验源代码】

#include <bits/stdc++.h>
using namespace std;

typedef char ElemType;
typedef struct BiTNode {
    ElemType data;//结点数据域
    struct BiTNode* lchild, * rchild;//结点指针域
//    bool isFirst;//非递归的后序遍历用来判断某结点是否第一次出现在栈顶
}BiTNode,*BiTree;


/*-------先序遍历二叉树T的递归算法---------*/
//返回值：叶子节点数
int preOrder(BiTree T) {
    int cnt = 0;
    //先序遍历的递归算法
    if (T) {
        cout << T->data;//访问根结点
        if(!T->lchild && ! T->rchild)
            return 1;
        cnt += preOrder(T->lchild);//先序遍历左子树
        cnt += preOrder(T->rchild);//先序遍历右子树
    }
    return cnt;
}

/*-------中序遍历的递归算法---------*/
void inOrder(BiTree T) {
    //中序遍历二叉树T的递归算法
    if (T)
    {
        inOrder(T->lchild);//中序遍历左子树
        cout << T->data;//访问根节点
        inOrder(T->rchild);//中序遍历右子树
    }
}

/*-------后序遍历二叉树T的递归算法-------*/
void postOrder(BiTree T) {
    if (T) {
        postOrder(T->lchild);//后序遍历左子树
        postOrder(T->rchild);//后序遍历右子树
        cout << T->data;//访问根结点
    }
}

/*-------层序遍历二叉树T的队列写法-------*/
void floorTraverse(BiTree T)
{
    queue <BiTree> q;
    if(T)
    {
        q.push(T);
    }
    while(!q.empty()){
        cout << q.front()->data;
        if(q.front()->lchild)
            q.push(q.front()->lchild);
        if(q.front()->rchild)
            q.push(q.front()->rchild);
        q.pop();
    }
}
/*-------按照题目条件手动创建二叉树-------*/
BiTree init() {
    BiTNode* root = new BiTNode;
    root->data = 'A';
    root->lchild = new BiTNode{'B',nullptr,nullptr};
    root->rchild = new BiTNode{'F',nullptr,nullptr};
    root->lchild->lchild = new BiTNode{'C'};
    root->lchild->lchild->lchild = new BiTNode{'D'};
    root->lchild->lchild->rchild = new BiTNode{'E'};
    
    root->rchild->lchild = new BiTNode{'G',nullptr,nullptr};
    
    return root;
}


int main()
{
    BiTree root = init();
    cout<<"先序遍历：";
    int cnt = preOrder(root);
    
    cout << endl;
    
    cout<<"中序遍历：";
    inOrder(root);
    cout << endl;
    
    cout<<"后序遍历：";
    postOrder(root);
    cout << endl;
    
    cout <<"叶子节点数为：" << cnt; 
    
    cout << "\n层序遍历：";
    floorTraverse(root);
    return 0;
}