Recommender System Review
- Overview
- Collaborative Filtering
- 基于用户的CF(User CF)
- 基于物品的CF(Item CF)
- Similarity Calculation
- Bias in CF
- Evaluation of Recommender System
- Factorization Machines
- Latent factor model
- LFM算法概述
- LFM算法原理介绍
- LFM算法应用场景
Overview
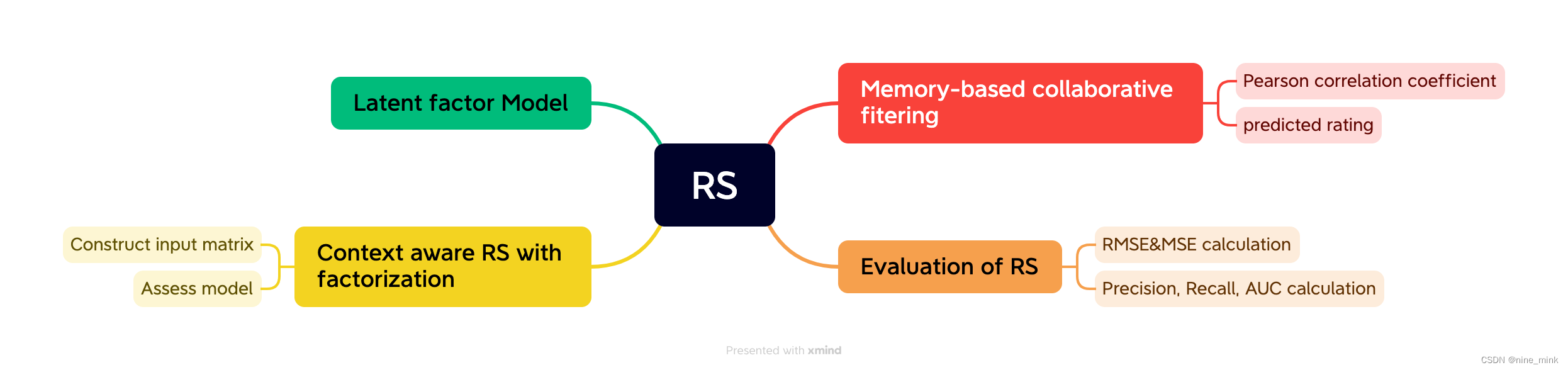
Collaborative Filtering
协同过滤是利用集体智慧的一个典型方法。要理解什么是协同过滤(Collaborative Filtering, 简称CF),首先想一个简单的问题,如果你现在想看个电影,但你不知道具体看哪部,你会怎么做?大部分的人会问问周围的朋友,看看最近有什么好看的电影推荐,而我们一般更倾向于从口味比较类似的朋友那里得到推荐。这就是协同过滤的核心思想。
协同过滤一般是在海量的用户中发掘出一小部分和你品位比较类似的,在协同过滤中,这些用户成为邻居,然后根据他们喜欢的其他东西组织成一个排序的目录作为推荐给你。
要实现协同过滤,需要一下几个步骤
- 收集用户偏好——如何收集决定推荐系统效果
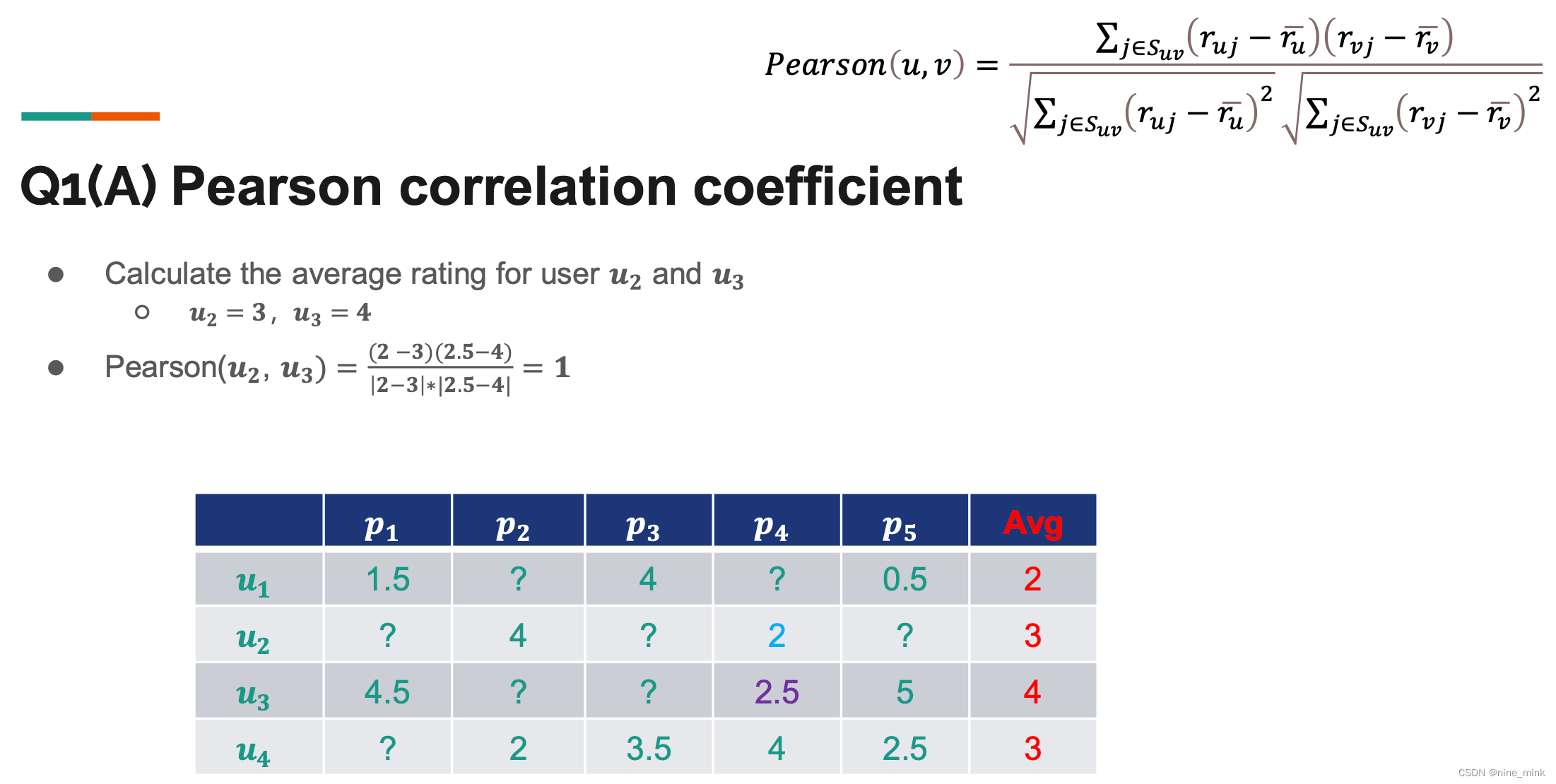
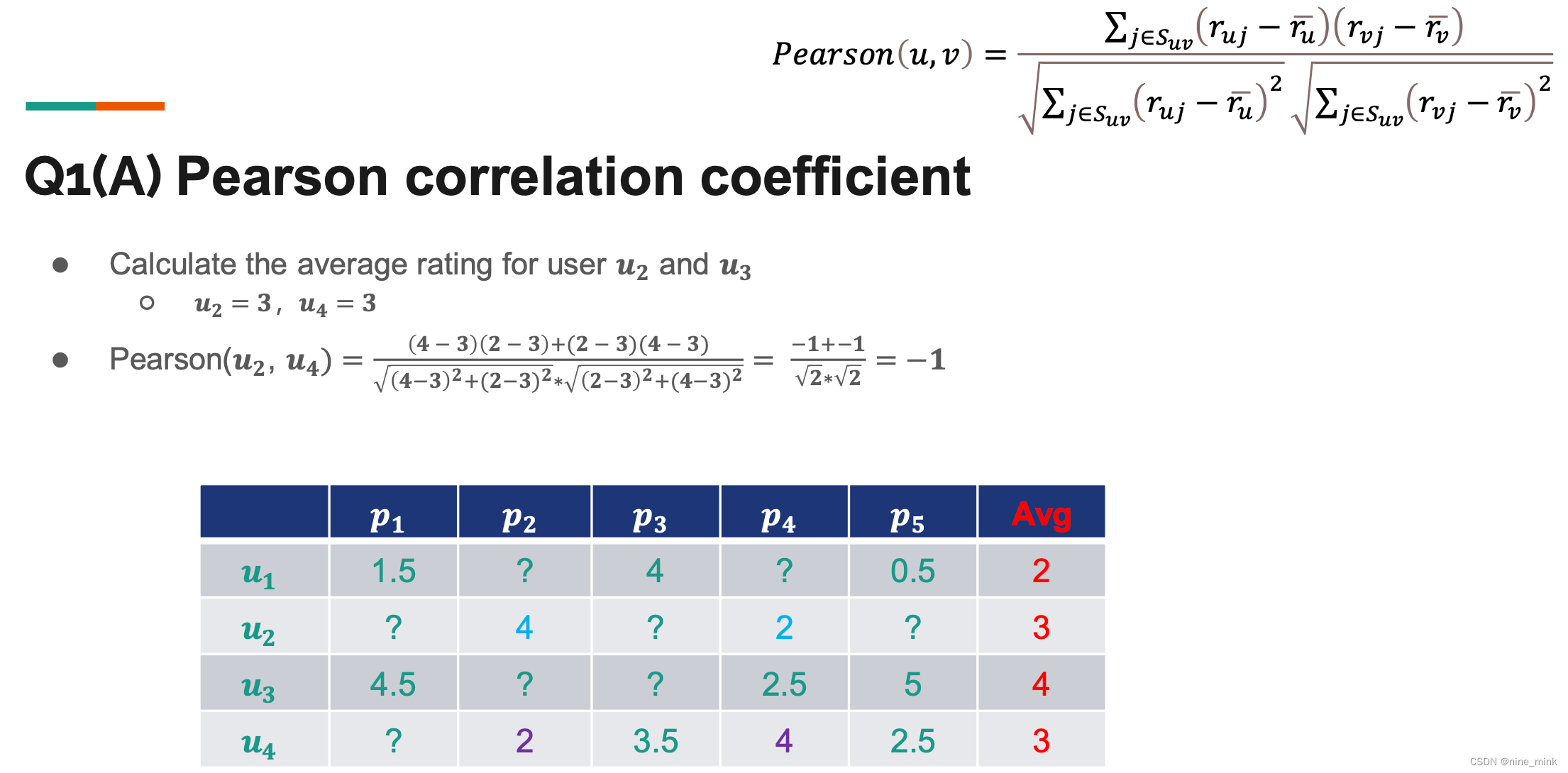
- 找到相似的用户或物品(Pearson Correlation Coefficient)
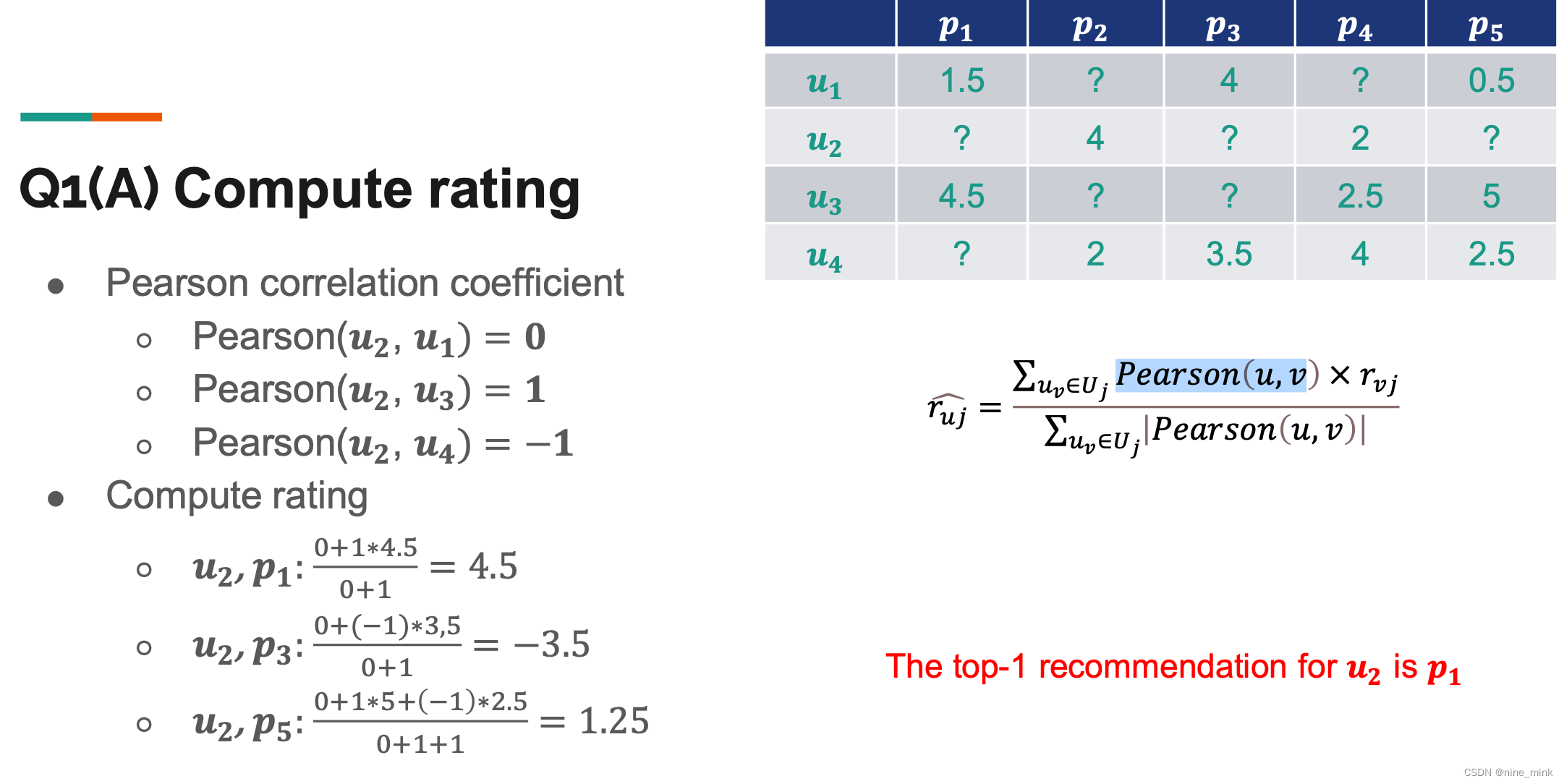
- 计算推荐(Collaborative Filtering)
基于用户的CF(User CF)
基于用户的CF 的基本思想相当简单,基于用户对物品的偏好找到相邻邻居用户,然后将邻居用户喜欢的推荐给当前用户。计算上,就是将一个用户对所有物品的偏好作为一个向量来计算用户之间的相似度,找到K 邻居后,根据邻居的相似度权重以及他们对物品的偏好,预测当前用户没有偏好的未涉及物品,计算得到一个排序的物品列表作为推荐。图2 给出了一个例子,对于用户A,根据用户的历史偏好,这里只计算得到一个邻居-用户C,然后将用户C 喜欢的物品D 推荐给用户A。
基于物品的CF(Item CF)
基于物品的CF 的原理和基于用户的CF 类似,只是在计算邻居时采用物品本身,而不是从用户的角度,即基于用户对物品的偏好找到相似的物品,然后根据用户的历史偏好,推荐相似的物品给他。从计算的角度看,就是将所有用户对某个物品的偏好作为一个向量来计算物品之间的相似度,得到物品的相似物品后,根据用户历史的偏好预测当前用户还没有表示偏好的物品,计算得到一个排序的物品列表作为推荐。图3 给出了一个例子,对于物品A,根据所有用户的历史偏好,喜欢物品A 的用户都喜欢物品C,得出物品A 和物品C 比较相似,而用户C 喜欢物品A,那么可以推断出用户C 可能也喜欢物品C。
Similarity Calculation
定义:Pearson correlation coefficient是一种衡量变量之间线性关系强弱的统计量。它的取值范围在-1到1之间,可以反映出两个变量之间的相关程度。如果相关系数接近1,表明两个变量之间存在完全正向的线性关系;如果接近-1,则说明存在完全负向的线性关系;如果接近0,则表示两个变量之间没有线性关系。
Pearson correlation coefficient的计算方法如下:
r = Cov(X, Y) / (σX * σY)
其中,Cov(X, Y)表示变量X和Y的协方差,σX和σY分别表示变量X和Y的标准差。通过计算协方差和标准差,我们可以得到两个变量之间的相关系数。


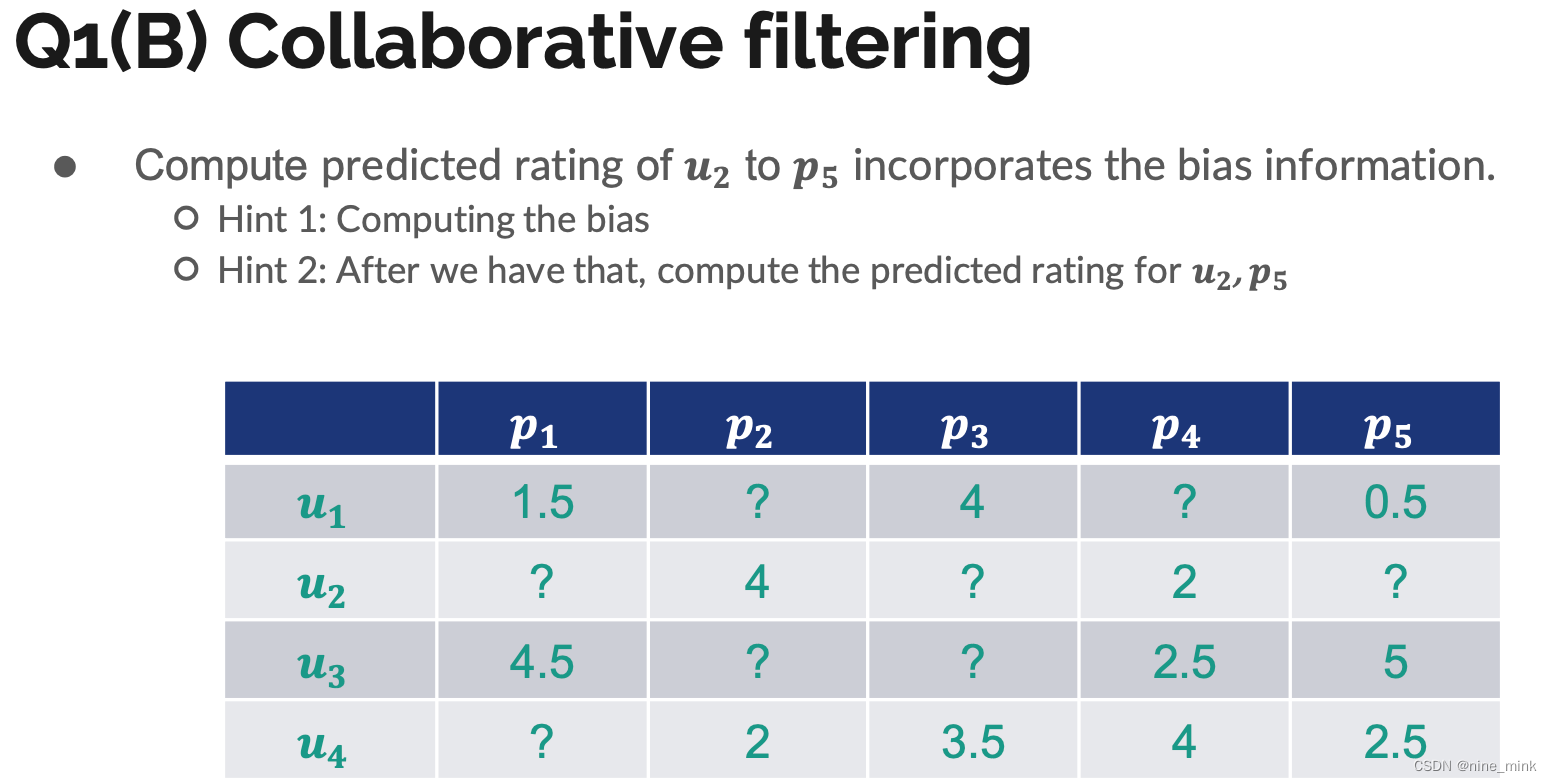
Bias in CF


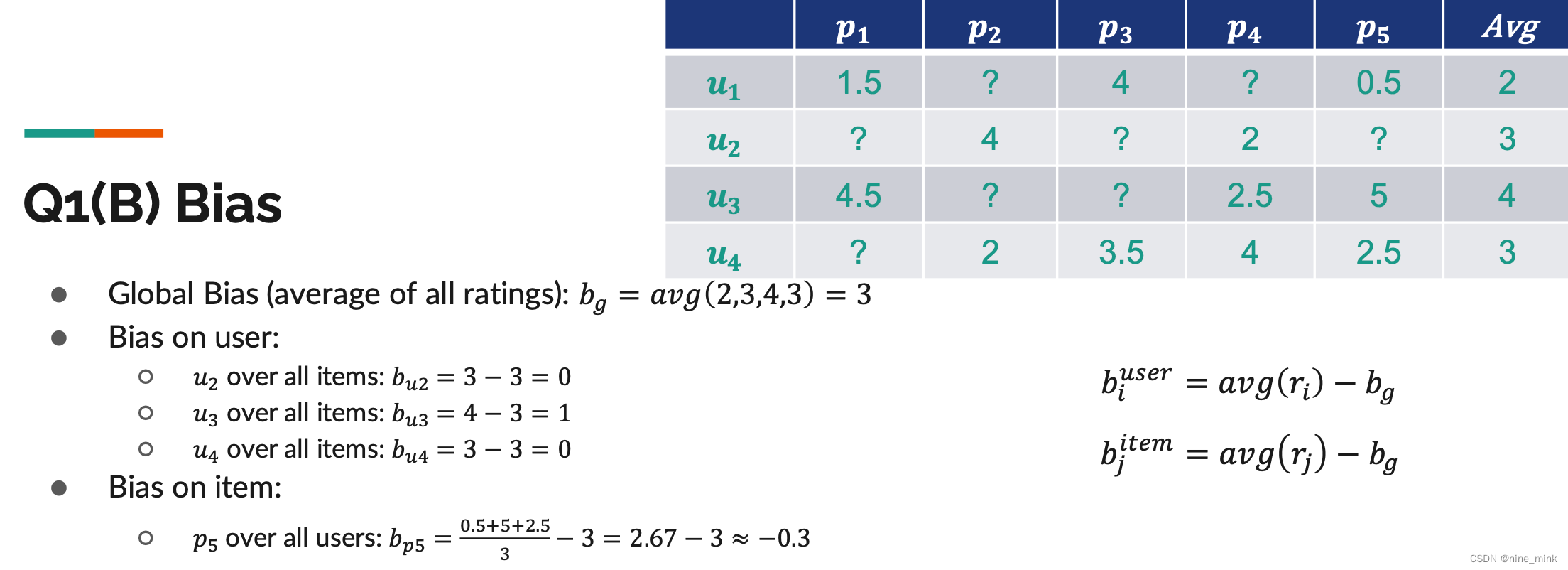
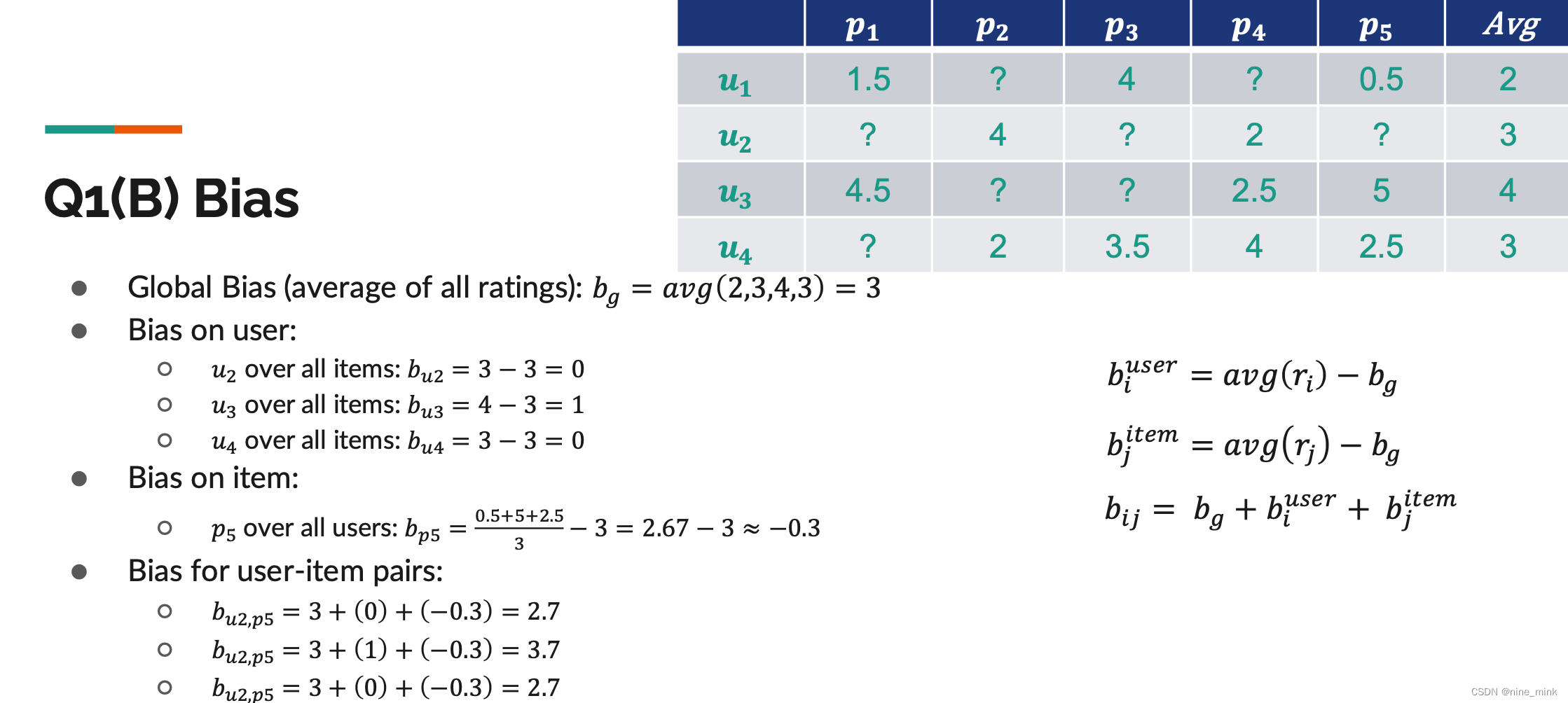
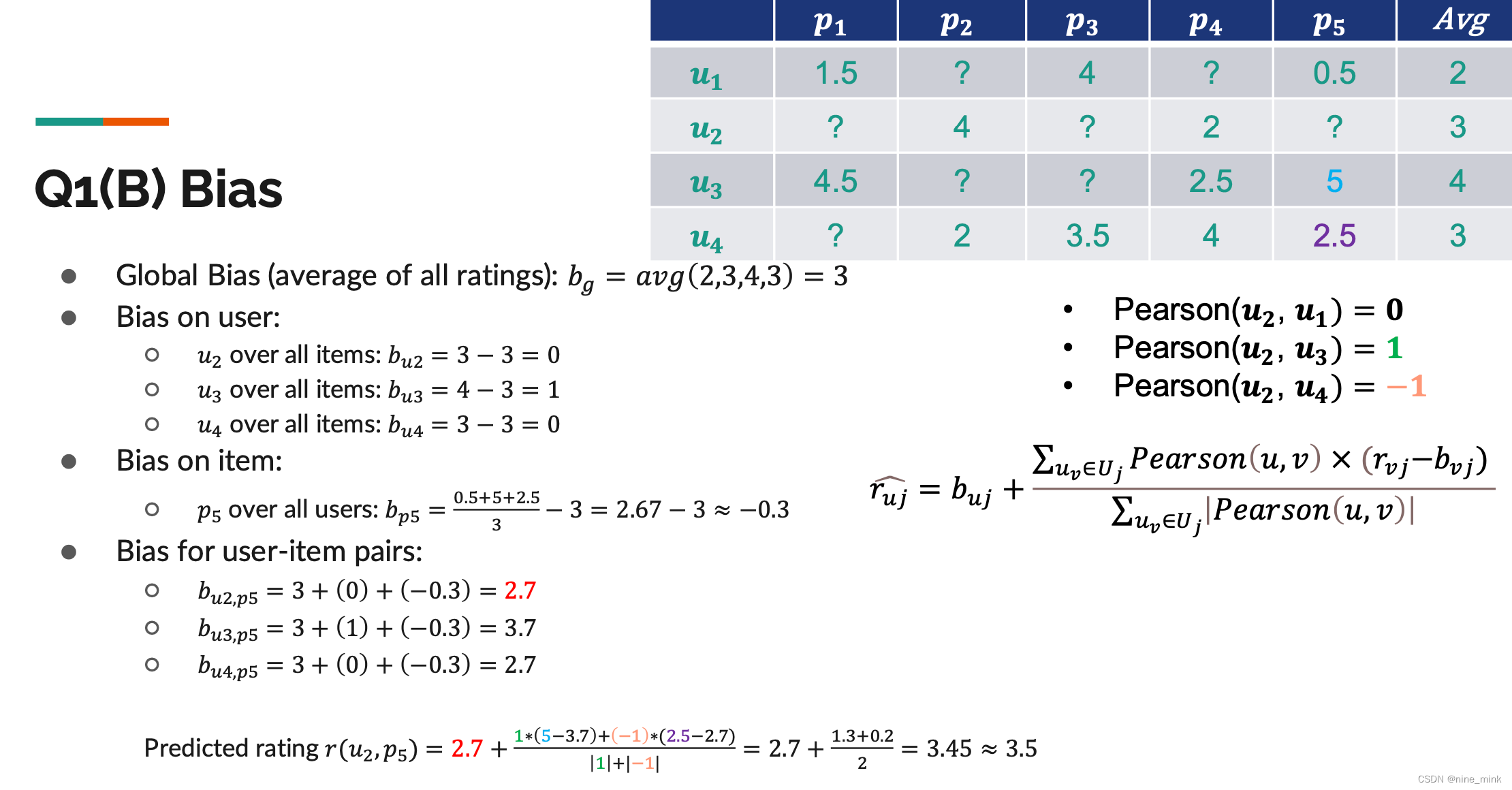
Evaluation of Recommender System





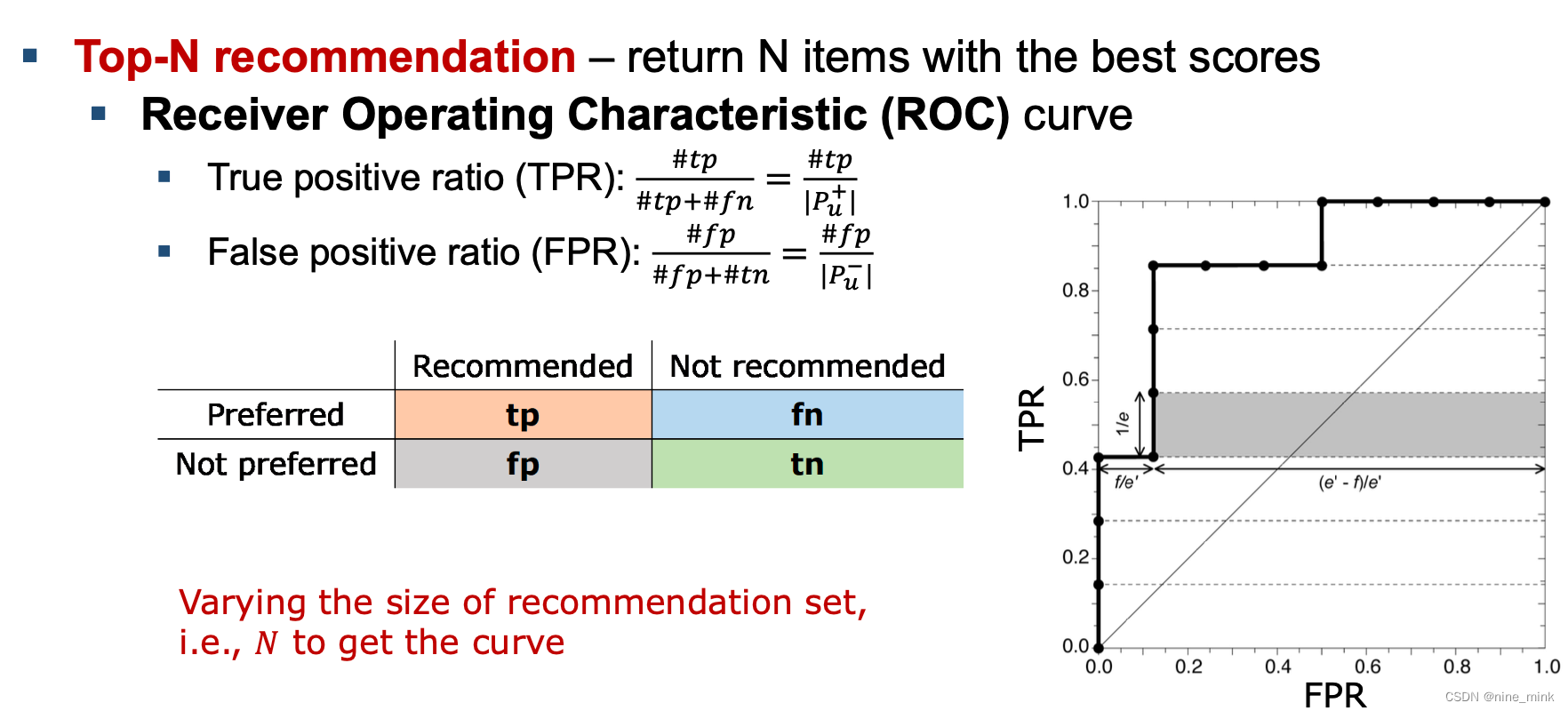




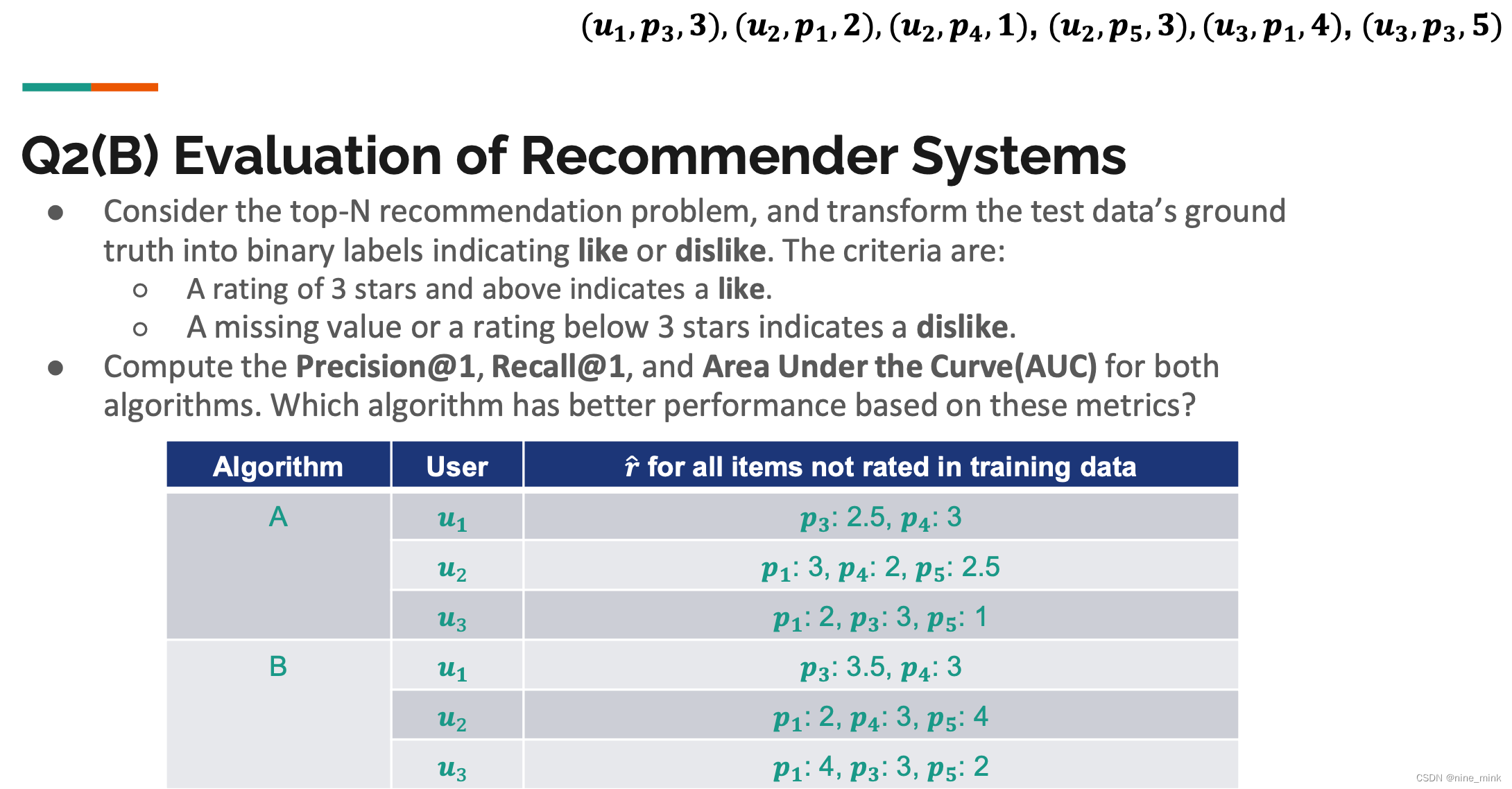




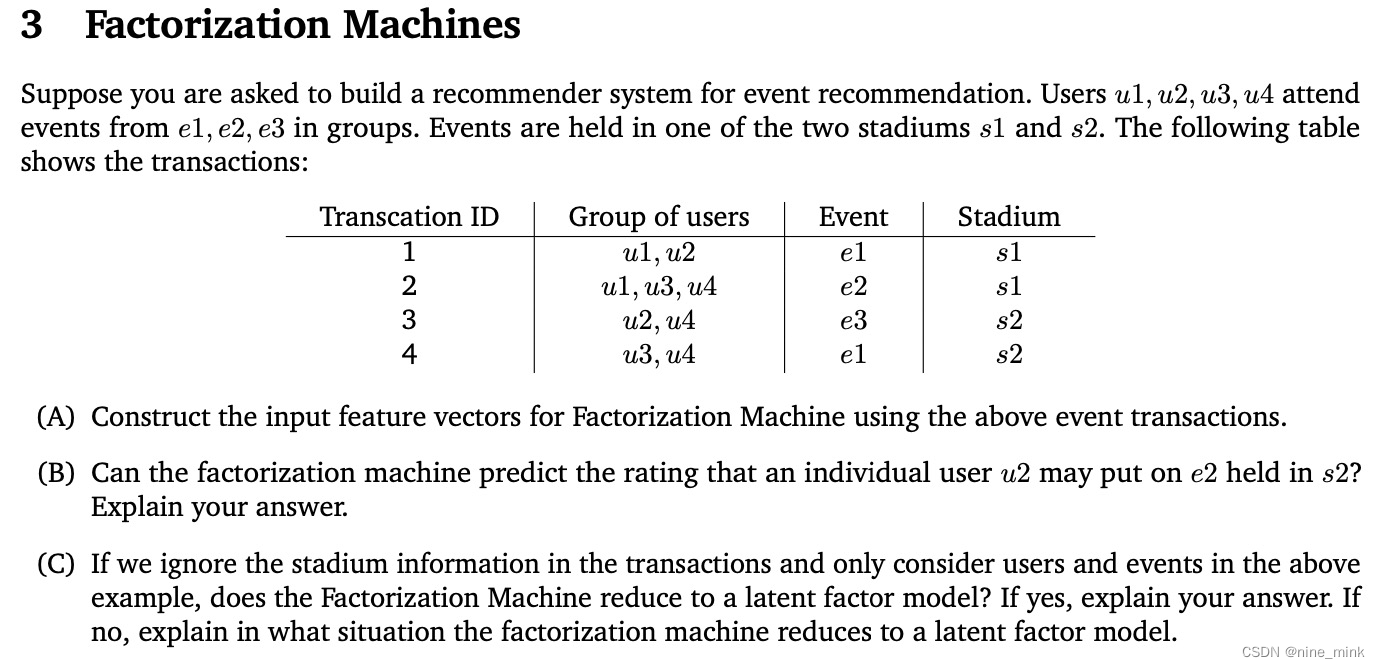
Factorization Machines
背景
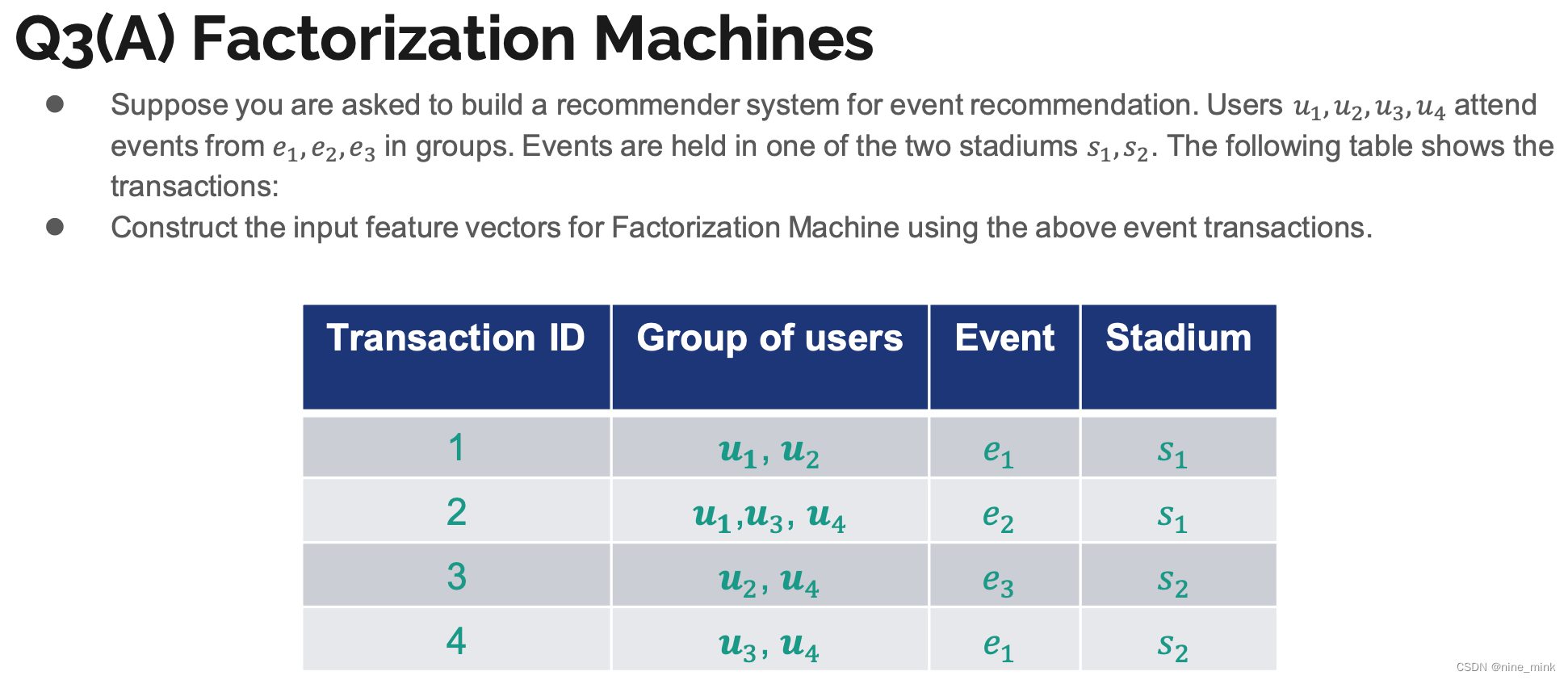
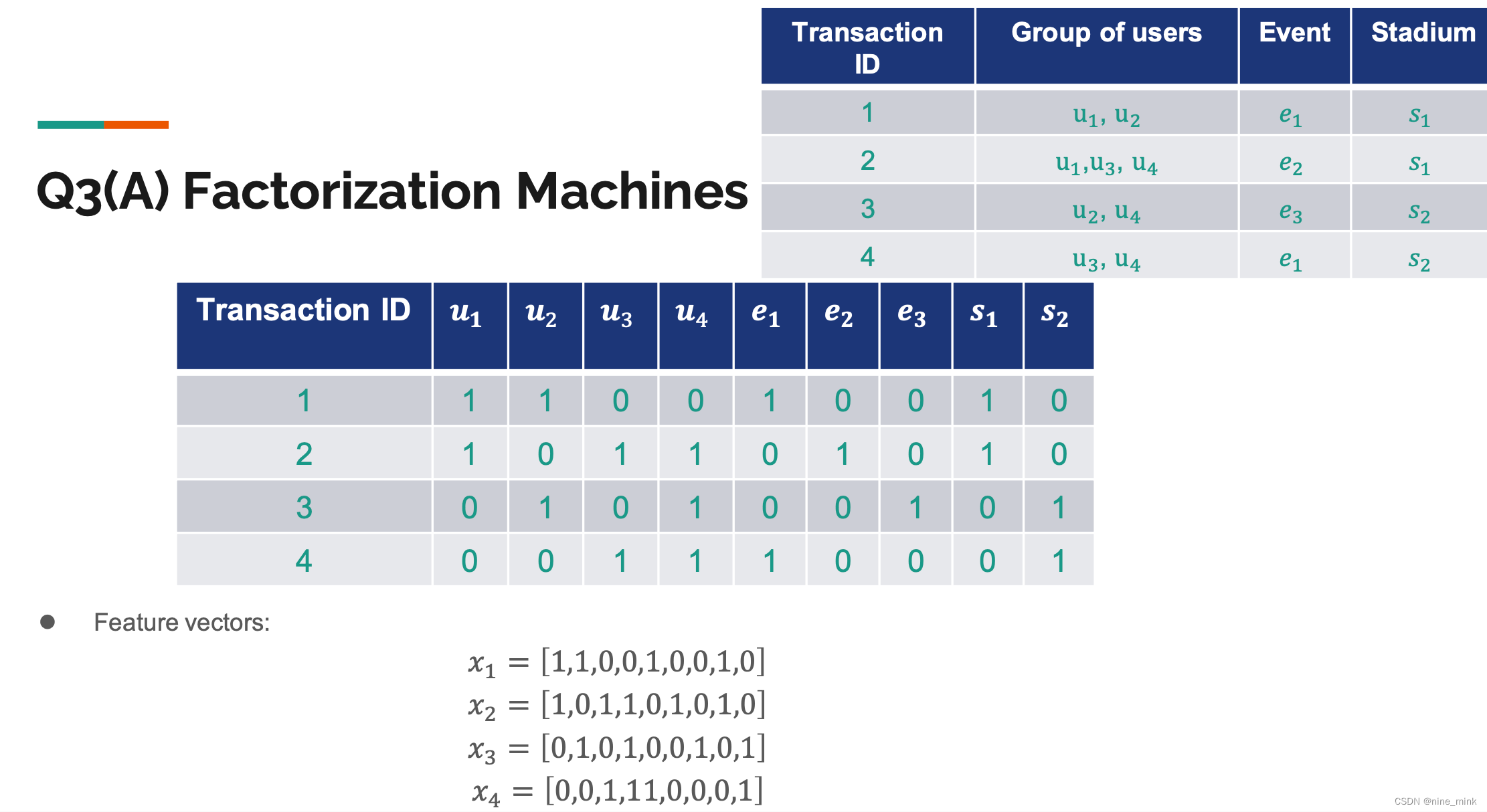
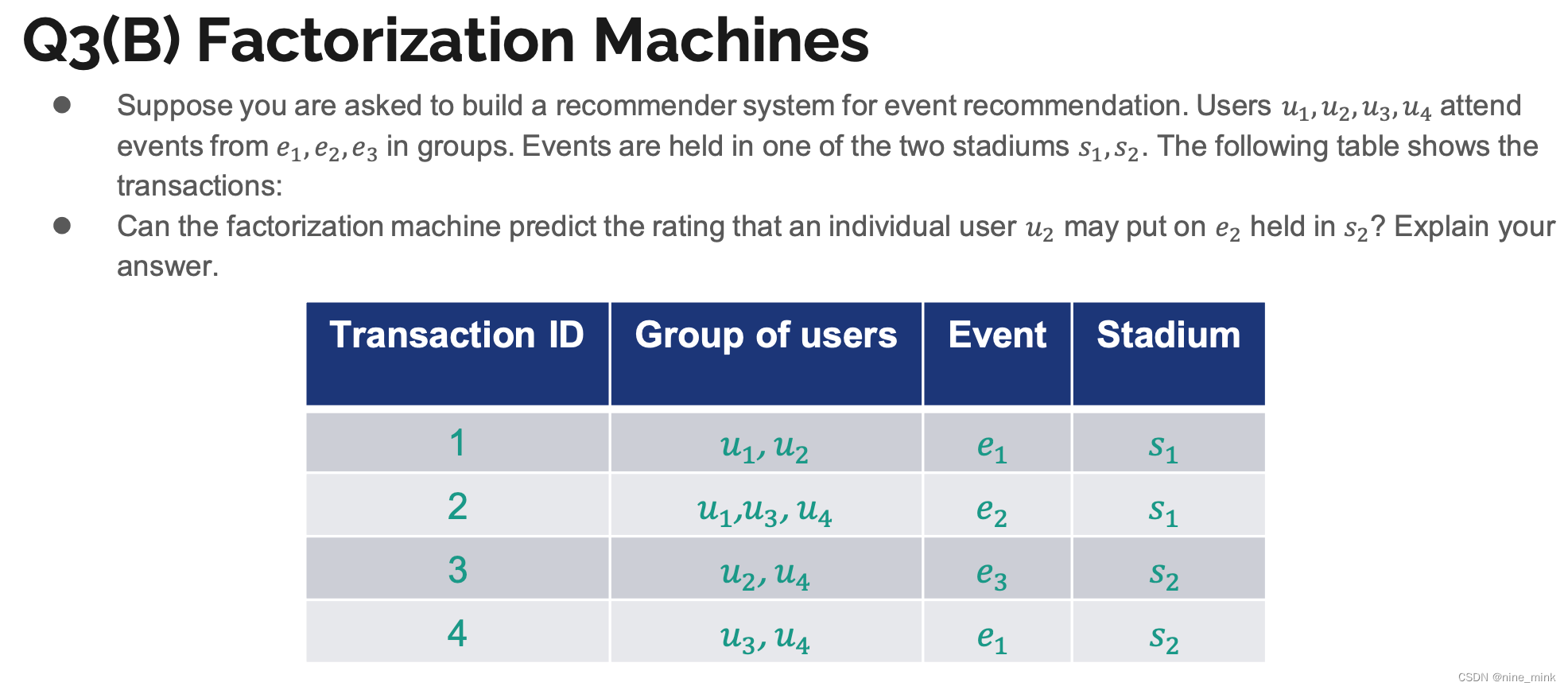
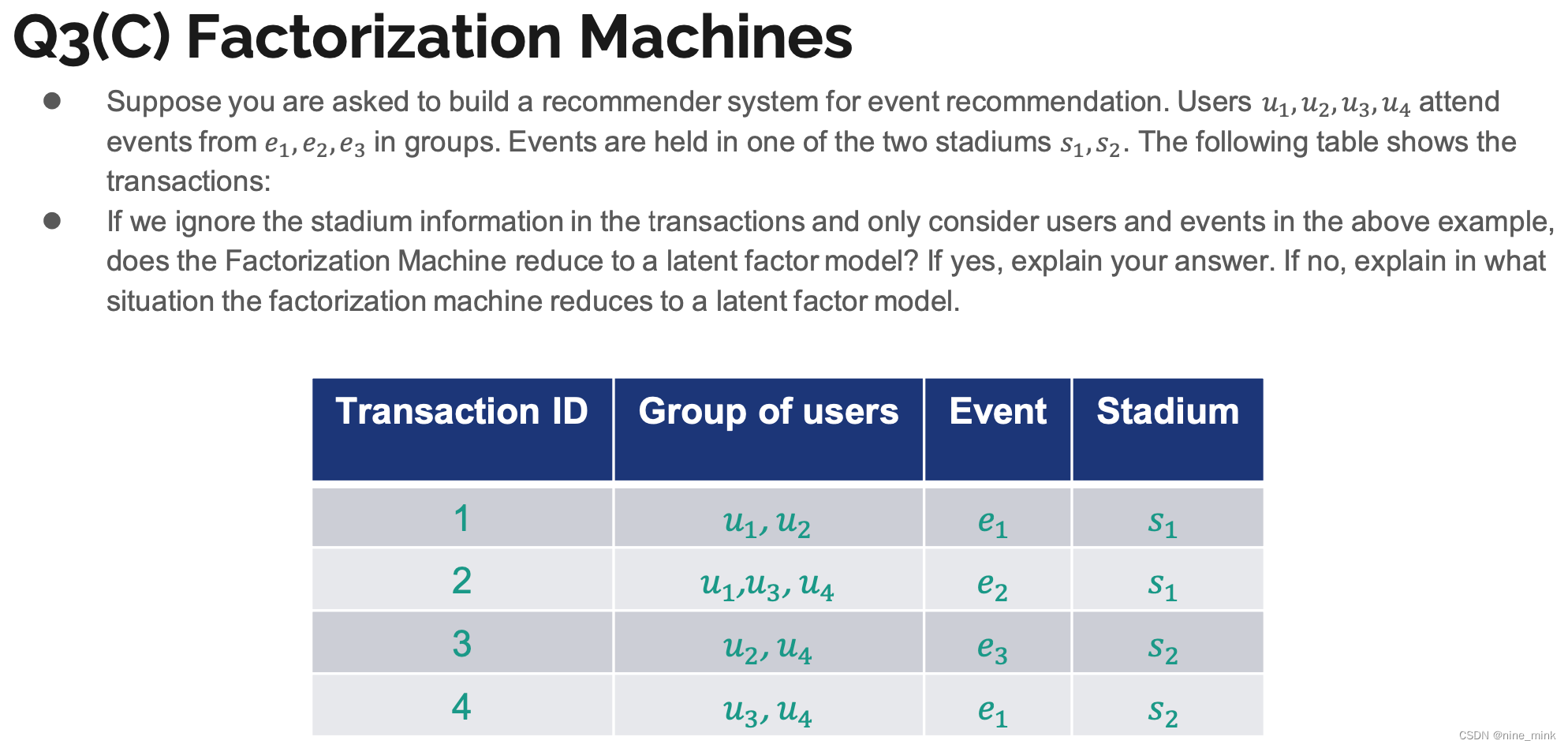
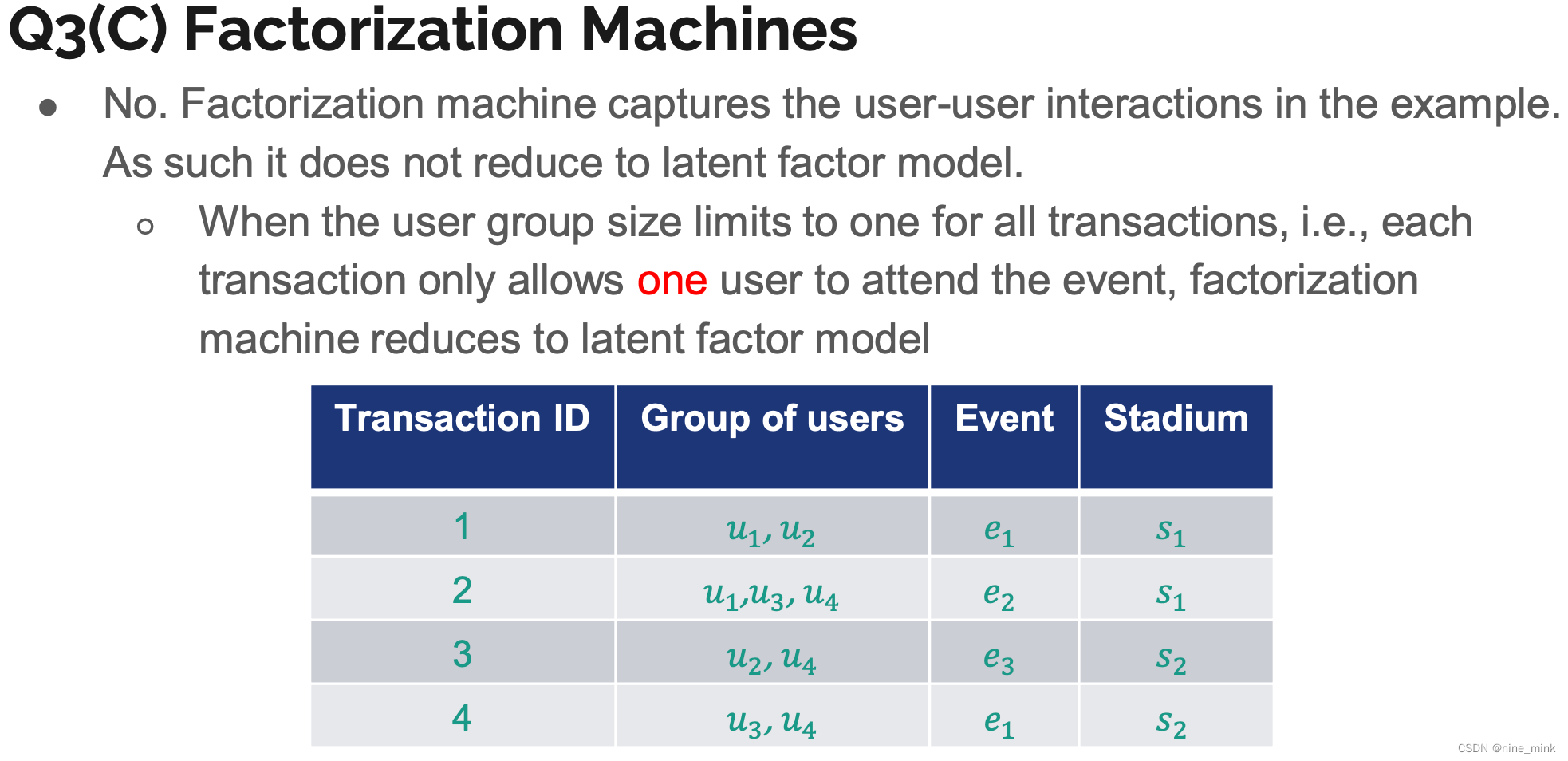
FM的适用对象是稀疏数据。
任何研究过点击预测问题或推荐系统的人都会面临类似的情况:由于数据集非常庞大,因此使用有限的计算资源对这些数据集进行预测变得非常困难。
但是,在大多数情况下,这些数据集是稀疏的(每个训练示例只有少数变量为非零)。在数据稀疏的情况下,满足求解参数都不为0的情况很少,所以很难训练。然而因子分解机有助于从从现有的原始数据中,提取最重要的潜在的或隐藏的特征。
一般来说,可以使用低维密集矩阵来表示对象和预测器之间关系,而分解有助于与前者建立大致相同的关联。
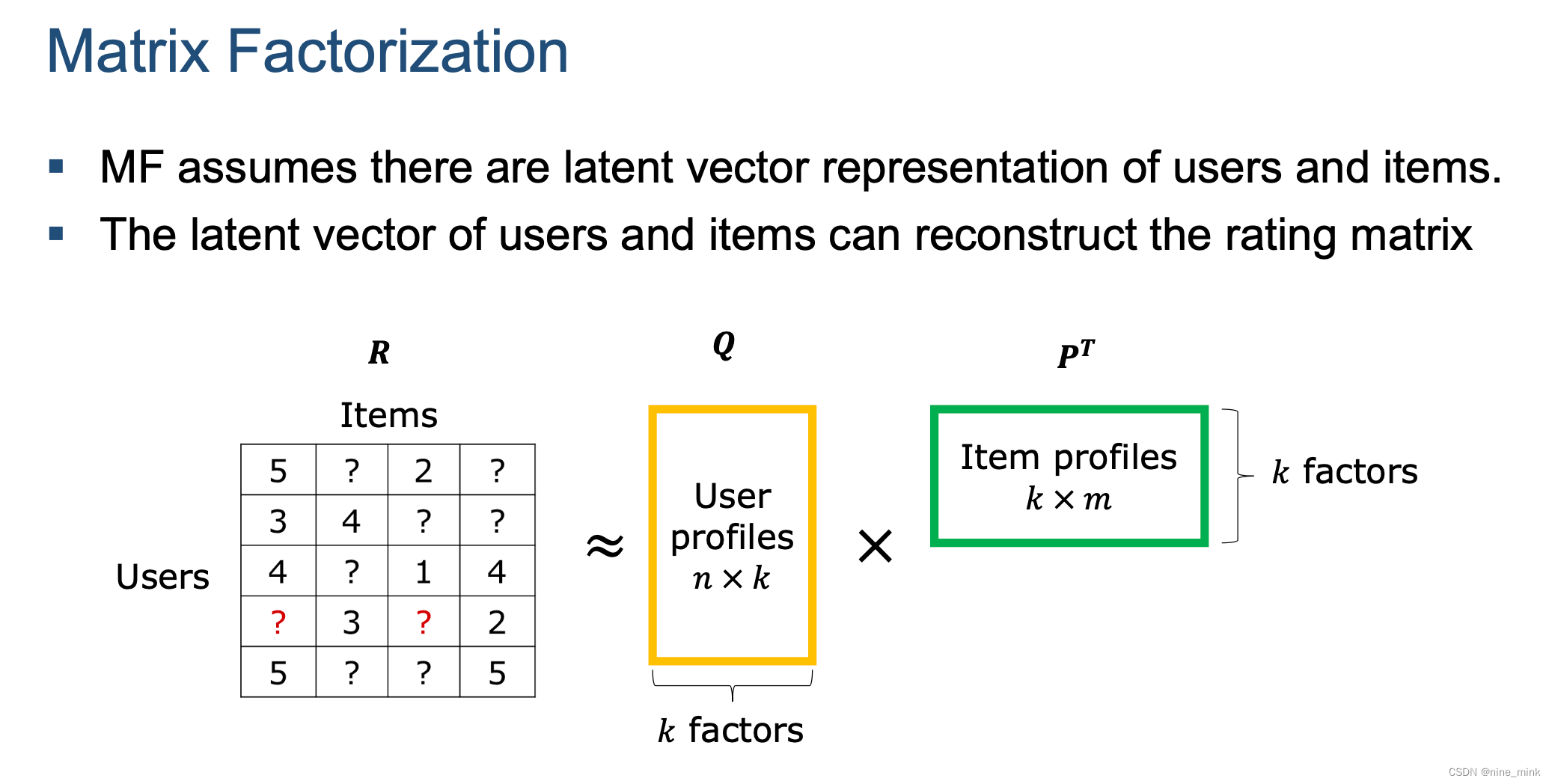
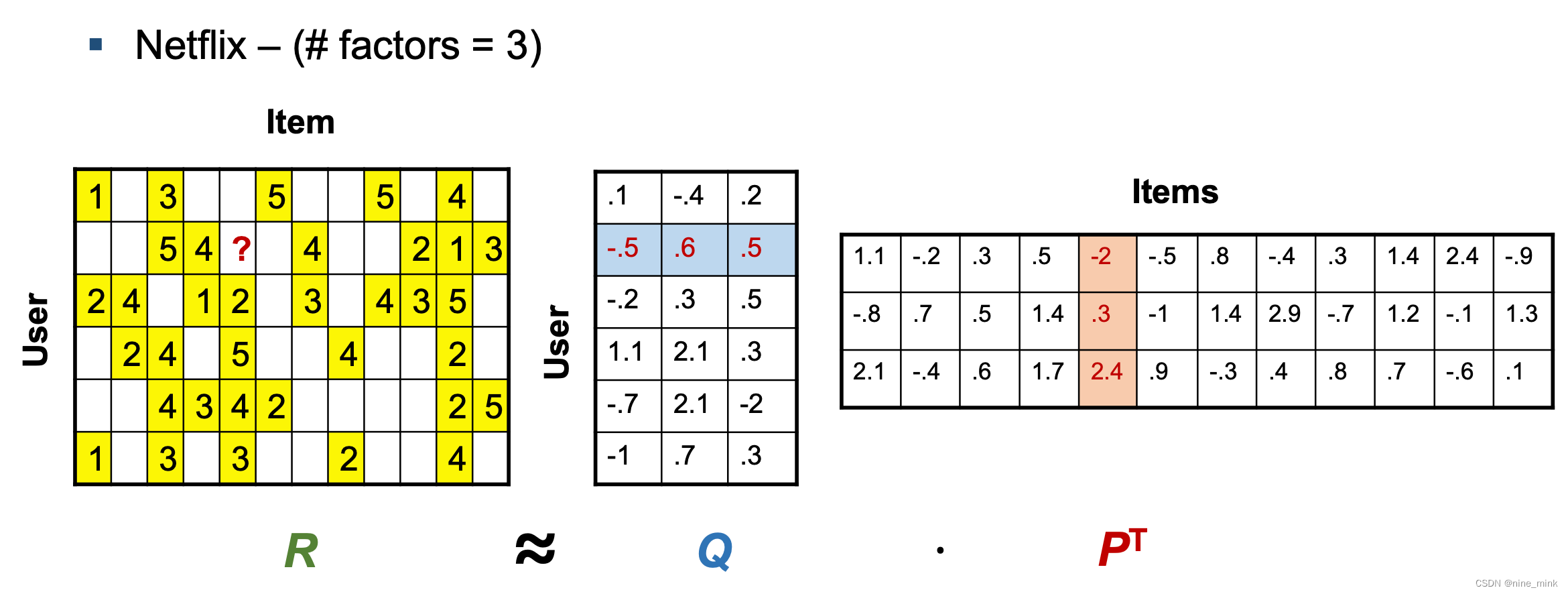



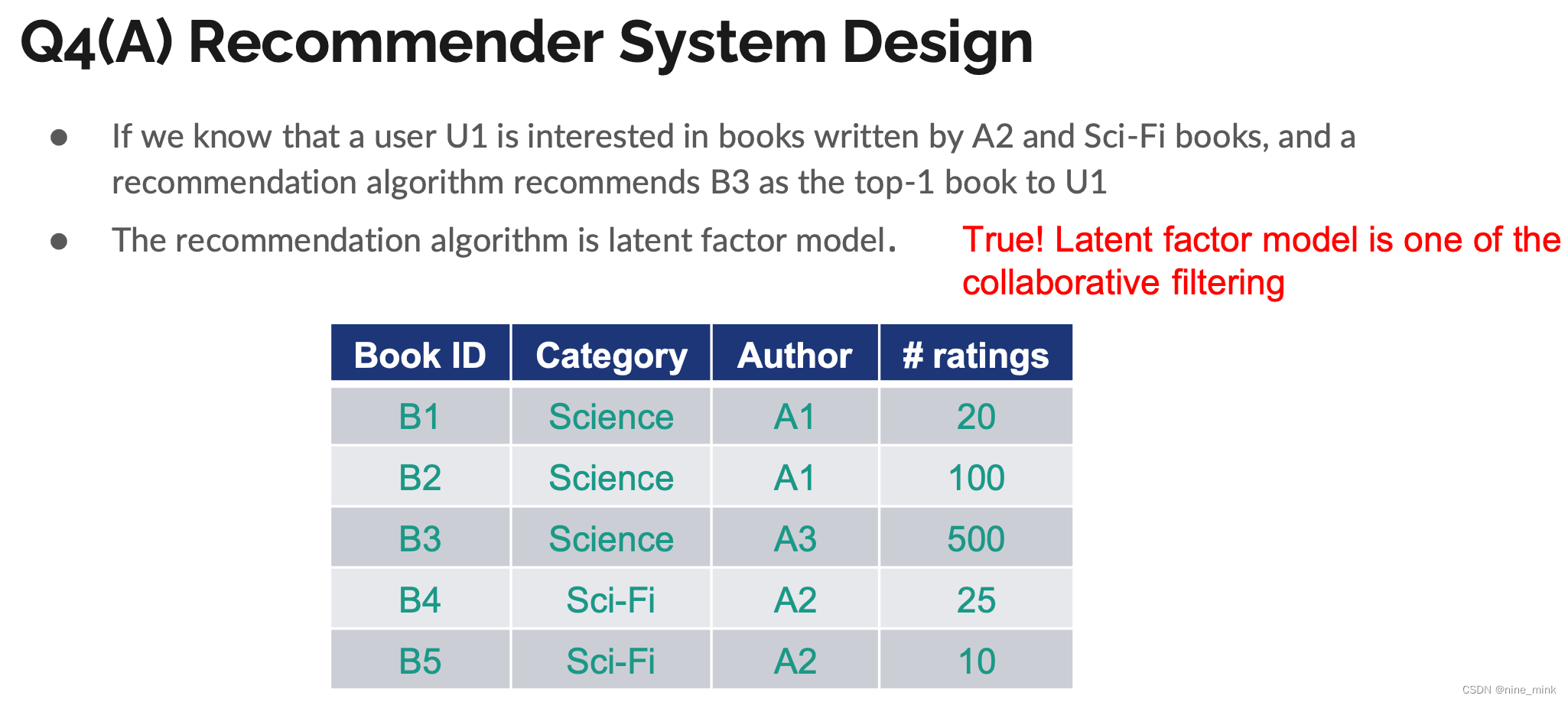
Latent factor model
LFM算法概述
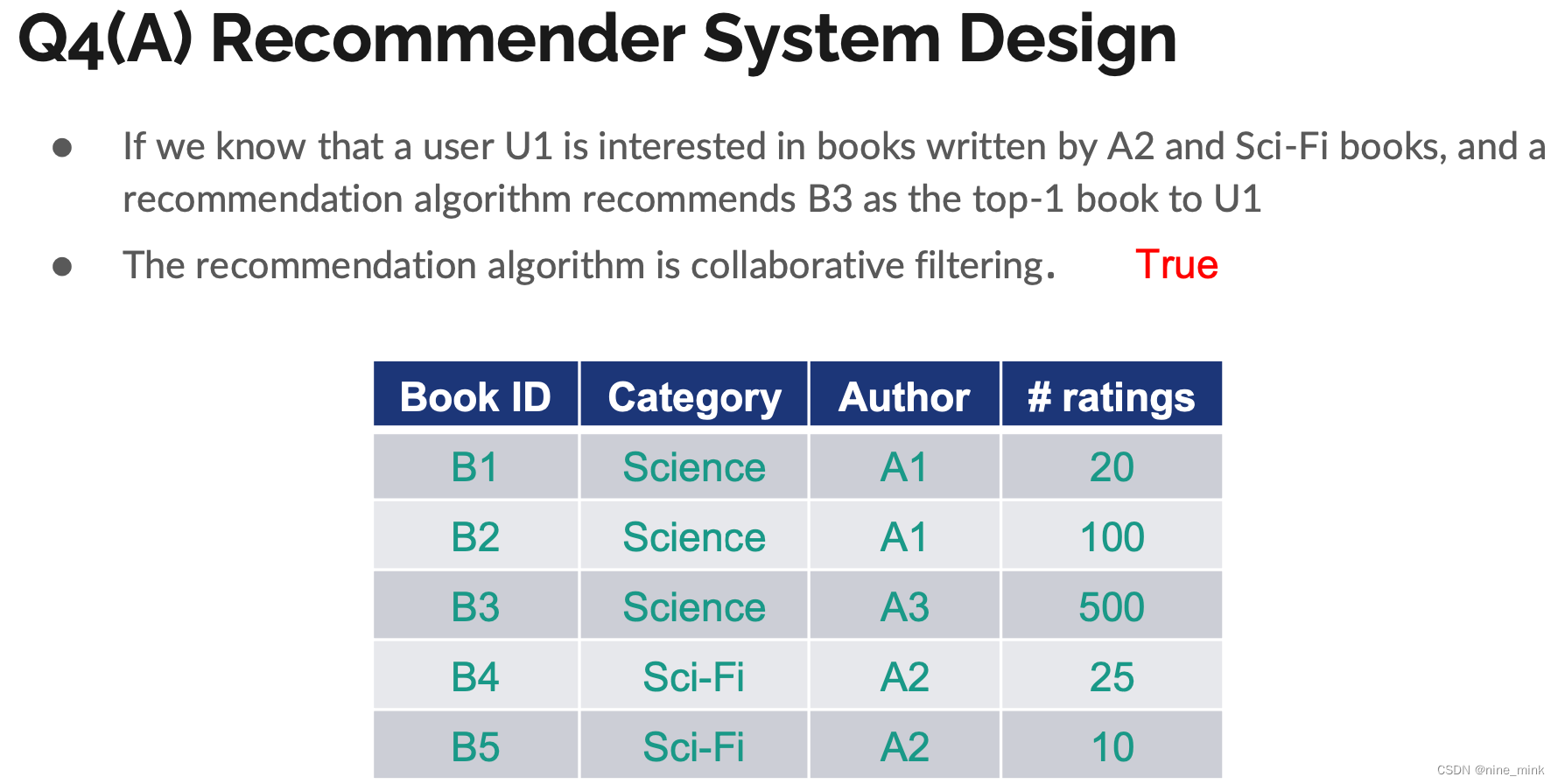
对于基于邻域的机器学习算法来说,如果要给一个用户推荐商品,那么有两种方式。一种是基于物品的,另一种是基于用户的。基于物品的是,从该用户之前的购买商品中,推荐给他相似的商品。基于用户的是,找出于该用户相似的用户,然后推荐给他相似用户购买的商品。
但是,推荐系统除了这两种之外,还有其他的方式。例如如果知道该用户的兴趣分类,可以给他推荐该类别的商品。
为了实现这一功能,我们需要根据用户的行为数据得到用户对于不同分类的兴趣,以及不同商品的类别归属。
LFM算法原理介绍
首先是数据的处理,由于使用的是隐性数据集,只有正样本,例如用户点击了某件商品,没有负样本。数据处理主要是选出数据集的负样本。
负样本的选取策略主要有以下要点:
(1)正负样本要均衡,基本保证正负样本的比例1:1
(2)负样本需要选择用户没有行为的热门商品。

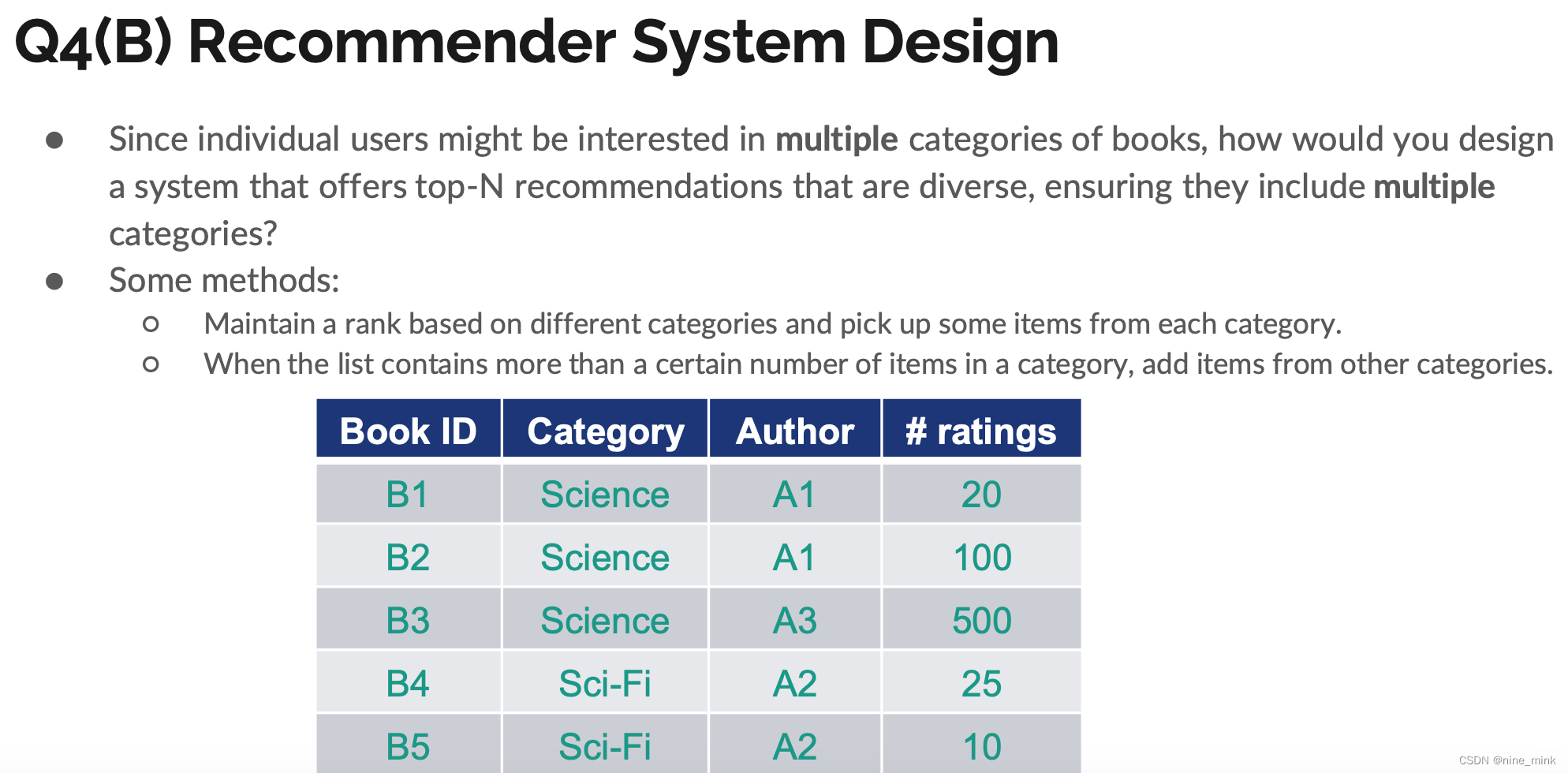
LFM算法应用场景
根据上述内容,可以得到相应的模型输出,即两个潜在因子矩阵。其中,潜在因子的维度是之前设定的,可以理解为你认为有哪些特征可能会影响user对item的喜好程度。
那么得到模型输出后,如何应用?
(1)计算用户toplike:对于与用户没有被展示的item,可以计算出一个用户对item的倾向性得分,取top即toplike,后直接完成用户对item的喜爱度列表,写入离线即可完成对在线的推荐。
(2)计算item的topsim:得到item的向量可以用很多表示距离的公式包括cos等等,计算出每一个item的相似度矩阵,该矩阵可以用于线上推荐。当用户点击item之后,给其推荐与该item的topsim item。
(3)计算item的topic:根据得到的item向量,可以用聚类的方法,如K-means等等,取出一些隐含的类别。也就是一些隐含的topic能将item分成不同的簇,推荐时按簇推荐。





![[PyTorch][chapter 59][强化学习-2-有模型学习]](https://img-blog.csdnimg.cn/af130b0190004921b6454f2662e18a7e.png)