学习目的

加餐 | 如何将非正态分布数据转换为正态分布的？手把手教你SPSS操作

软件版本

IBM SPSS Statistics 26。

原始文档

《小白爱上SPSS》课程
#统计原理

将非正态分布数据转换为正态分布

在前面我们学过的参数检验中，比如两独立样本T检验和单因素方差分析中，有一个重要前提条件是连续型变量要满足正态分布。
如果遇到非正态分布数据怎么办？
一种建议是选用合适的非参数检验方法，比如两样本秩和检验；另一种是对原始进行转换使得其满足正态分布特性。
这一讲，我们来讲解下如何转换？

一、正负偏态的转换方法

正态分布转换方法有很多，比如：对数变换、平方根变换、平方根反正弦变换、平方变换、倒数变换、Box-Cox变换、正态得分法。
这里选择几种常用方法讲解，起示范作用。
数据转换分成两种情况，一种是正偏态数据，另一种是负偏态数据，每种又分成轻度、中度和严重三种情况。

（一）正偏态数据转换方法

1、轻度正偏态分布
当偏度值>0，偏度值为其标准误差的2-3倍，即Z-score=2~3，此时认为资料分布呈现轻度的正偏态分布，故考虑对变量x取根号开平方的方法来进行转换。
SPSS语句如下：
COMPUTE x_new = SQRT(x)
（SQRT为开平方根Square Root缩写）
2、中度正偏态分布
当偏度值>0，偏度值为其标准误差的3倍以上时，即Z-score>3，此时认为资料分布呈现中度的正偏态分布，可以考虑对变量x取对数来进行转换。可以取自然对数（ln）或以10为底的对数（log10）。
SPSS语句如下：
COMPUTE x_new = LN(x)
COMPUTE x_new = LG10(x)
注意：LG10的纠正力度较强，有时甚至会矫枉过正，将正偏态转换为负偏态，因此在进行正态转换后一定要对该变量再次进行正态性检验。
3、重度正偏态分布
对于两端波动比较大的数据资料，极端值可能产生较大的影响，此时可以考虑取倒数的方法来进行转换。
SPSS语句如下：
COMPUTE x_new = 1/x
若你不太熟悉SPSS语法编辑窗口，则可通过SPSS中“转换”—“计算变量”实现，找到sqrt, ln, lg10等函数。

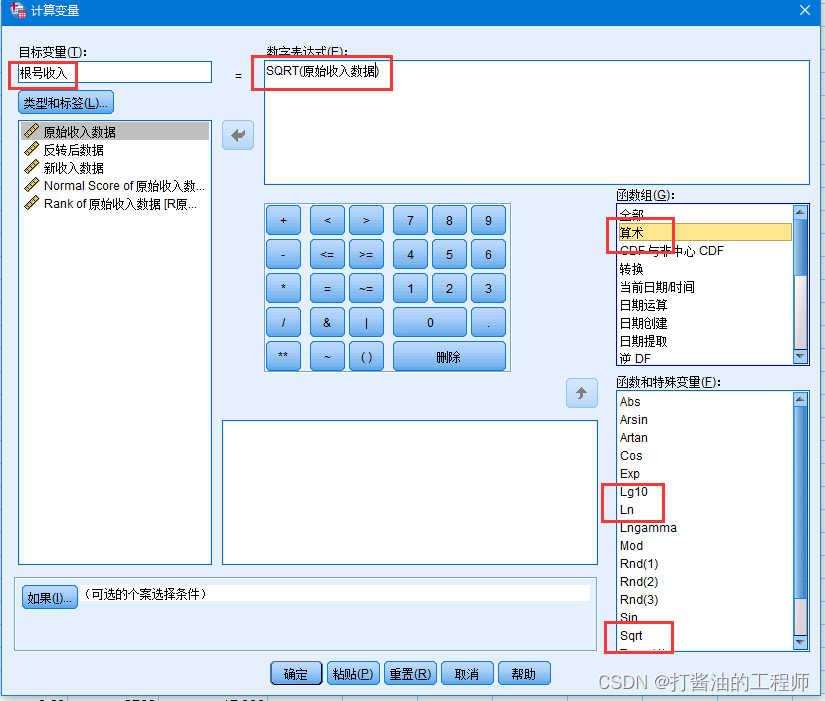
注意：根号下要求数据均为非负数（即≥0），对数要求数据均为正数（即>0）；取倒数要求分母不为0, 如果变量x中出现上述情况，则需要先将其进行一定的转换，如x+K或K-x，再对其取根号、对数或倒数。其中K为一个常数，可以根据需要进行赋值，例如赋值为1，或取数据的最小值、最大值等。

（二）负偏态数据转换方法

对于负偏态分布的数据资料，首先需要将负偏态资料进行反转，转换为正偏态，然后再参考正偏态分布资料的转换方法进行转换。
反转的方法：首先找出该数据系列的最大值max，用最大值+1，再减去每个数值。
1、轻度负偏态分布
SPSS语句如下：
COMPUTE x_new = SQRT(max+1-x)
2、中度负偏态分布
SPSS语句如下：
COMPUTE x_new = LN(max+1-x)
COMPUTE x_new = LG10(max+1-x)
3、重度负偏态分布
SPSS语句如下：
COMPUTE x_new = 1/(max+1-x)
二、实战案例
下面是42名员工的月收入，试检验其正态性。若不服从正态性，请将其转化为正态分布。
读数据：

GET 
  FILE='E:\E盘备份\recent\小白爱上SPSS\小白数据\加餐：非正态分布数据的转换.sav'. 

三、正态性检验

这里主要通过SPSS的探索性描述统计方法来考察收入的分布情况。

（一）操作如下

点击分析——描述统计——探索
将“收入”选入因变量列表，点击 图 --勾选直方图–勾选含检验的正态图–继续–确定。
命令行：

EXAMINE VARIABLES=原始收入数据
  /PLOT HISTOGRAM NPPLOT /*若无此行，则不输出正态性检验表*/
  /COMPARE GROUPS 
  /STATISTICS DESCRIPTIVES 
  /CINTERVAL 95 
  /MISSING LISTWISE 
  /NOTOTAL.

（二）结果解读

1.描述看峰度偏度


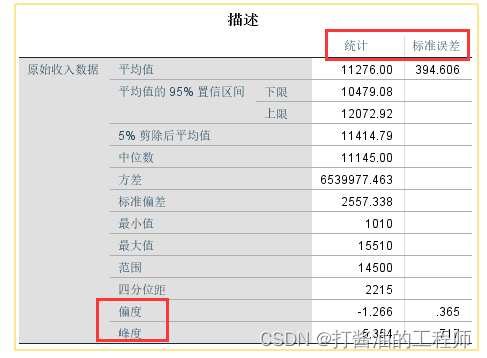
由以上结果可知，偏度系数的绝对值均大于1.96，可以认为该组样本数据不服从符合正态分布。
4.看正态性检验结果

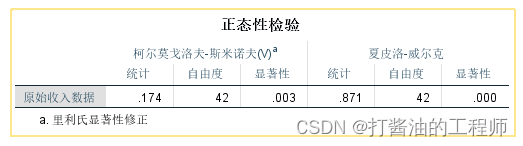
5.结果解读：
当数据量≤50时，倾向于以夏皮洛-威尔克（S-W）检验结果为准；
当数据量>50时，倾向以柯尔莫戈洛夫-斯米诺夫（K-S）检验结果为准；当数据量>5000时，SPSS只会显示K-S检验结果。
本例中，我们检验40名员工收入的正态分布情况，由上表显示，样本量（可参考自由度那一列数值）小于50，故以夏皮洛-威尔克（S-W）检验结果为准。检验的p值（即显著性那一列）为0.000，小于0.05，具有统计意义，不支持原假设。说明40名员工收入不符合正态分布，故认为收入不满足正态性。

四、SPSS：对数转换法

（一）选择检验方法和操作步骤

由上可知，因本案例中偏度值<0，为负偏态，偏度值为其标准误差的3倍以上，故考虑对变量x取对数来进行转换。对于负偏态分布的数据资料，首先需要将负偏态资料进行反转，转换为正偏态，然后再参考正偏态分布资料的转换方法进行转换。
Step1：反转的方法为：首先找出该数据系列的最大值max，用最大值+1，再减去每个数值，本例子中最大值为15510，处理后数据名称为“反转后数据”如下：

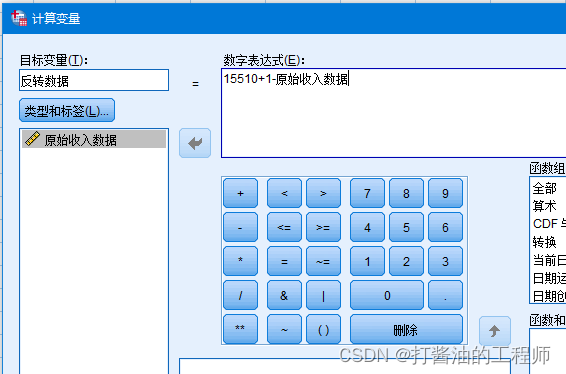
命令行：

COMPUTE 反转数据=15510+1-原始收入数据. 
EXECUTE.

处理结果如下：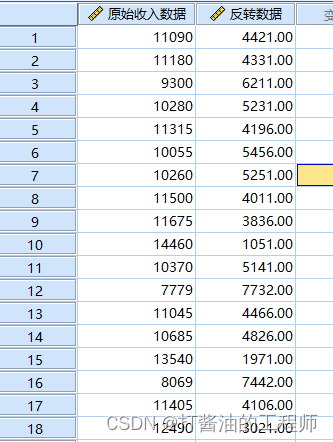
Step2: 对反转后数据进行对数转换，以Log10为例，步骤如下：
(1) 选择转换→ 计算变量
(2) 在目标变量（T）框中输入一个新的变量名：新收入数据，作为数据转换后的变量名，此处设定为新收入数据。
(3) 在函数组中选择算数，在函数和特殊变量中双击Lg10，此时在数字表达式框中显示LG10（？）
(4) 从变量列表中双击反转后数据，此时在数字表达式框中显示：LG10（反转数据）

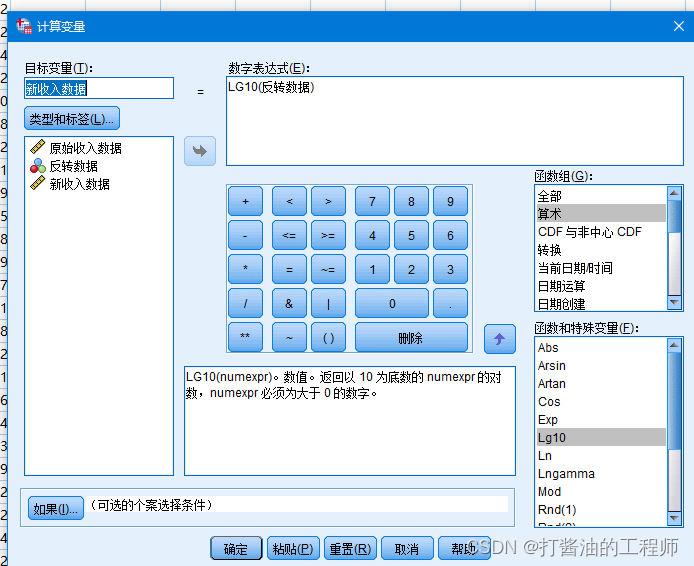
(5) 点击确定完成操作，操作完成，出现新收入数据列。
命令行：

COMPUTE 新收入数据=LG10(反转数据). 
EXECUTE.

（二）结果验证和解读

重新验证正态性：

EXAMINE VARIABLES=新收入数据
  /PLOT HISTOGRAM NPPLOT /*若无此行，则不输出正态性检验表*/
  /COMPARE GROUPS 
  /STATISTICS DESCRIPTIVES 
  /CINTERVAL 95 
  /MISSING LISTWISE 
  /NOTOTAL.

结果：

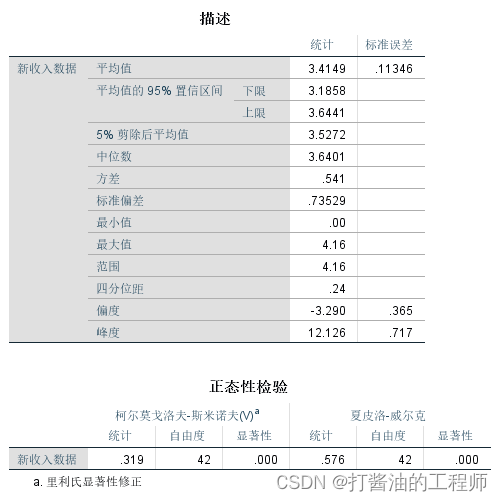
在结果输出的描述表格中显示，计算偏度系数和峰度系数均大于1.96，正态性检验p<0.001,故说明转换后数据仍不服从正态分布（读者可以采用【倒数】转换方法尝试下，结果仍然不服从正态分布）。
至此，本公众号建议不进行正态分布数据转换，而采用非参数检验方法。因为，一般而言，收入这个变量的总体数据是不服从正态分布的。
当然，我们也可采用正态得分方法操作，使其转换为正态分布。

五、SPSS:正态得分法

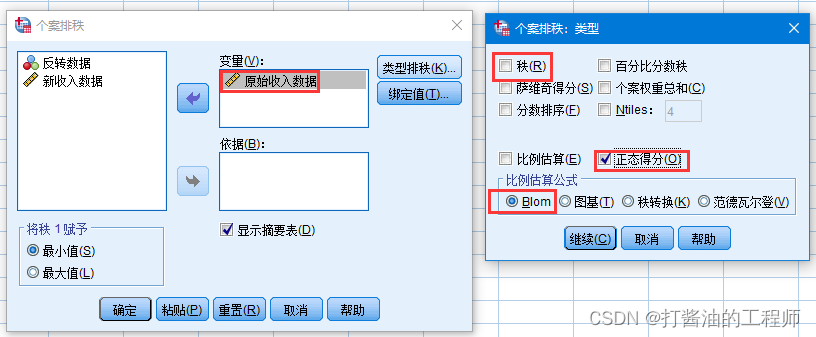
（一）选择转换→个案排秩检验
将原始收入数据选入变量(V)框中，点击类型排秩选项框，取消默认勾选的秩，勾选正态得分选项。在比例估算公式下有4种方法可供选择，默认Blom方法，其他方法也可以进行尝试，点击继续再点击确定完成操作。

命令行：

RANK VARIABLES=原始收入数据 (A) 
  /NORMAL 
  /PRINT=YES 
  /TIES=MEAN 
  /FRACTION=BLOM.

我们可以看到在程序运行后在变量列表中多出了一个名为N原始的新变量，即为计算的正态得分。

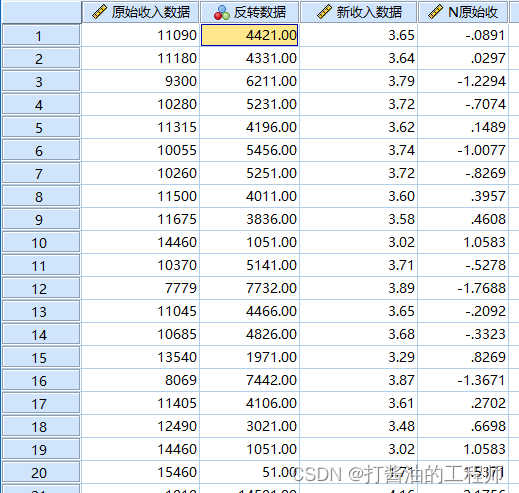
重新验证正态性：

EXAMINE VARIABLES=N原始收
  /PLOT HISTOGRAM NPPLOT /*若无此行，则不输出正态性检验表*/
  /COMPARE GROUPS 
  /STATISTICS DESCRIPTIVES 
  /CINTERVAL 95 
  /MISSING LISTWISE 
  /NOTOTAL.

下图为采用探索方法对N原始收入数据正态性检验以验证转化效果。


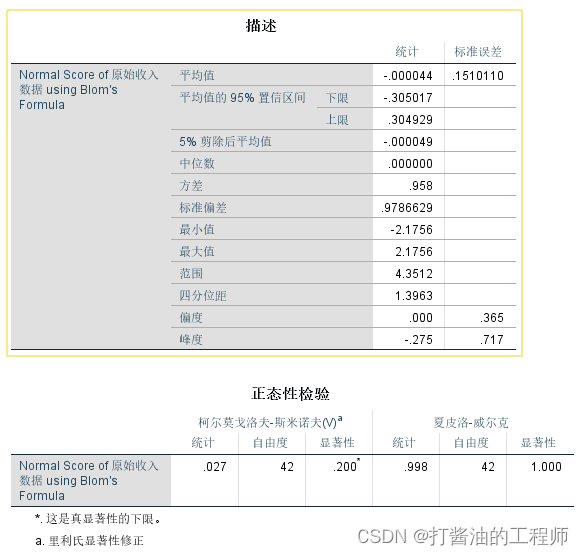
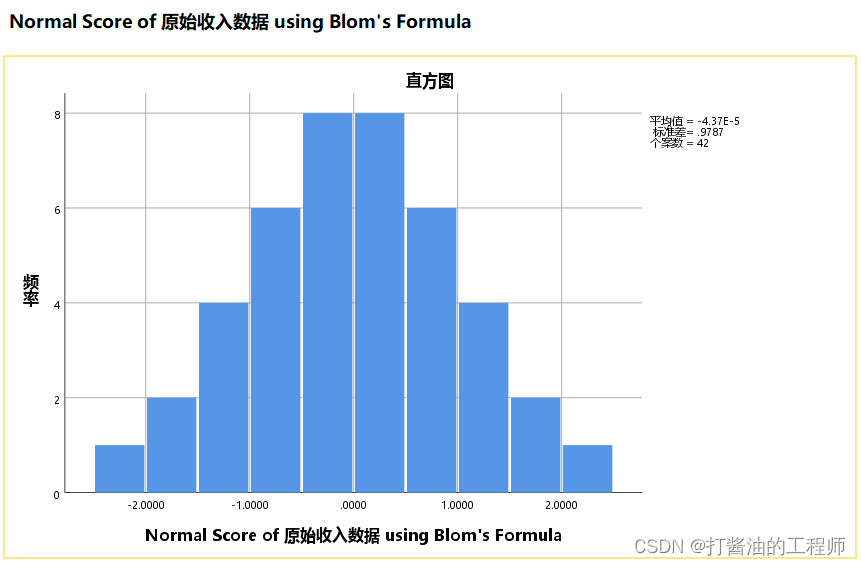
在结果输出的描述表格中显示，偏度系数和峰度系数均小于1.96，正态性检验p=1.000>0.05,故说明转换后数据服从正态分布。

需要注意

基于正态得分法得到的数据，在编秩过程中额外地加入原本不属于数据本身的分布特征，因此在一般统计方法中，并不能直接当做正态数据使用，其标准差、方差等信息与原始数据的计算结果也并不一样。这种转换，仅能用作在构建复杂模型时的探索。

六、划重点

（1）正态分布转换方法有很多，包括：对数变换、平方根变换、平方根反正弦变换、平方变换、倒数变换、Box-Cox变换（SPSS软件实现不了）和正态得分法等。
（2）不是任何非正态数据都可以进行正态转换，只有把握认为数据的总体分布是正态的时候才可做正态转换。
（3）如果一种正态分布转换方法没成功，则需要多次其他转换方法，甚至要创造性提出转换方法，从中选择效果较好者。
（4）如果通过多次变量转换的方法依然无法转换成功，就不再适用于T检验、方差分析等方法了，这时可采用前期介绍过的非参数检验的方法来进行分析，例如Wilcoxon检验和Mann-Whitney U检验方法等。
（5）在对线性回归模型进行解释时，如果使用函数转换的方法对变量进行转换，则应对转换后的变量给予解释，或者可以根据转换时使用的函数关系，倒推原始自变量对原始因变量的效应大小。