java入门，java数据结构二叉树结构

一、前言

树结构是计算机各种存储和查询算法的基本结构。但是在学习这个数据结构的时候，很少人知道它有什么运用，因为在学的时候，也是纯数学的讲解。博主当时学的时候也是云里雾里，最经典的就是严蔚敏和吴伟民的那本《C语言数据结构》。首先这个这个数据结构以树的结构来形象比喻这是一个巨大的错误。因为自然界几乎找不到和它所描述的数据结构的真实的树。而且它还是一棵倒置的树。特别是二叉树，我几乎没见过在自然界中的树长成二叉树的，因为这种树台完美了。所以这种比如完全是个错误，还有树结构里有混用了父，子，一下子叶子一下子父子的这些玩意，让人不知道这个是人还是树，第二，就是上数据结构这门课中没有讲清楚这种树结构在程序中如何运用。甚至现在我才知道树结构用在数据库的索引上的例子。

二、树结构

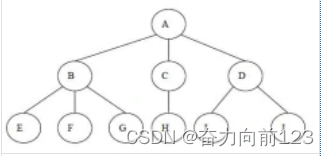
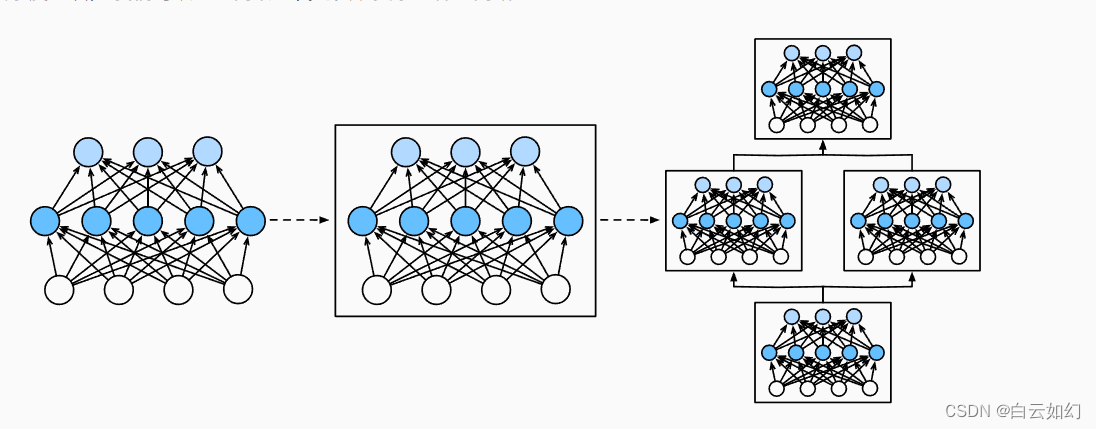
这种结构就是树结构，但是它不够完美，我们需要完美的二叉树。

我们要的是这种

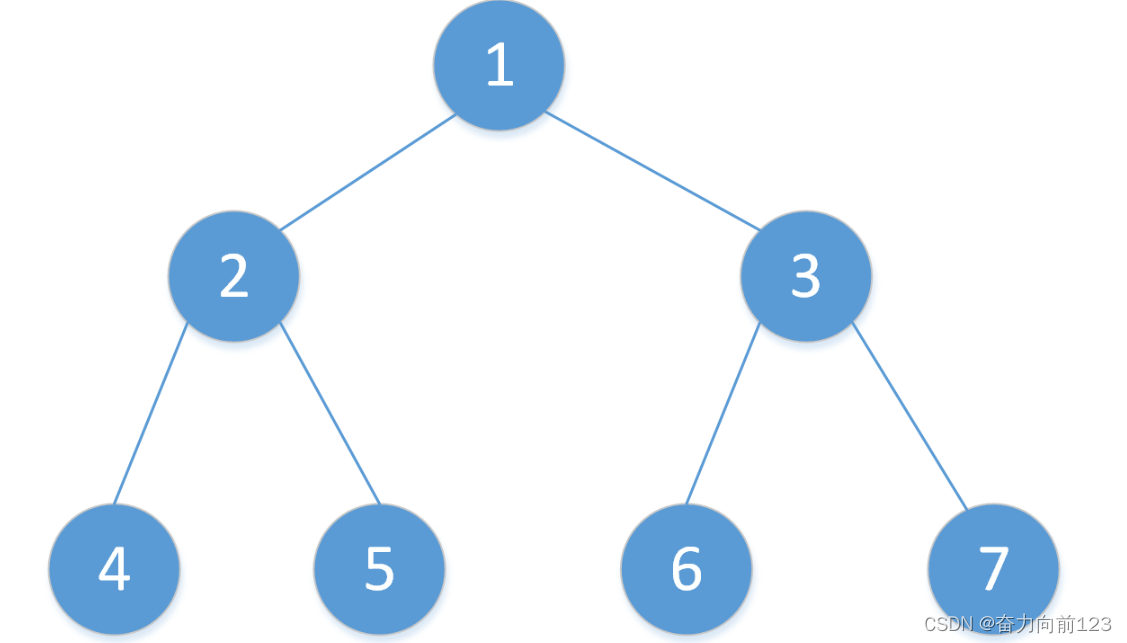
三、二叉树

二叉树（binary tree）是指树中节点的度不大于2的有序树，它是一种最简单且最重要的树。二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树

二叉树（Binary tree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树，且有左右之分。

二、为什么使用树结构

以前我也不明白为什么使用树结构，用线性表不就行了吗？后来才发现，数结构可以存足够多的元素，同时它的查询效率更高。

1、二叉树是n个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成，是有序树。当集合为空时，称该二叉树为空二叉树。在二叉树中，一个元素也称作一个节点。

2、有多少种二叉树

二叉树，完全二叉树，满二叉树，二叉排序树，平衡二叉树，红黑树，B树，B+树，B*树

1、完全二叉树

一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树

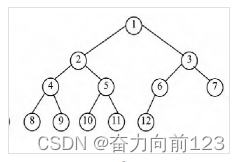
2、满二叉树

一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的深度为K，且结点总数是(2^k) -1 ，则它就是满二叉树。

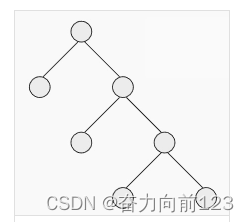
3、平衡二叉树

平衡二叉树也叫 AVL 树。平衡二叉树是具有以下特点的二叉查找树：它是一棵空树或它的左右两个子树的高度差的绝对值不超过 1，并且左右两个子树都是一棵平衡二叉树。

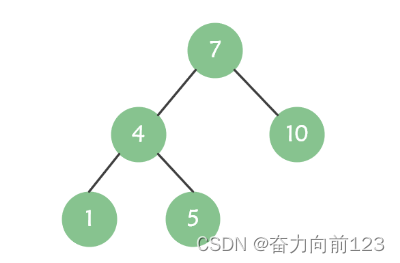
4、红黑树

红黑树（Red Black Tree）是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。
红黑树是在1972年由Rudolf Bayer发明的，当时被称为平衡二叉B树（symmetric binary B-trees）。后来，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。
红黑树是一种特化的AVL树（平衡二叉树），都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。
它虽然是复杂的，但它的最坏情况运行时间也是非常良好的，并且在实践中是高效的：它可以在O(log n)时间内做查找，插入和删除，这里的n 是树中元素的数目。

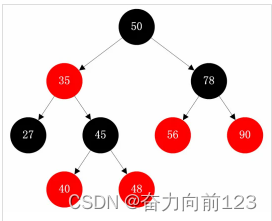
5.B树

一棵m阶B树(balanced tree of order m)是一棵平衡的m路搜索树。它或者是空树，或者是满足下列性质的树：

1、根结点至少有两个子女；

2、每个非根节点所包含的关键字个数 j 满足：┌m/2┐ - 1 <= j <= m - 1；

3、除根结点以外的所有结点（不包括叶子结点）的度数正好是关键字总数加1，故内部子树个数 k 满足：┌m/2┐ <= k <= m ；

4、所有的叶子结点都位于同一层。

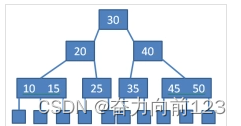
6、B+树

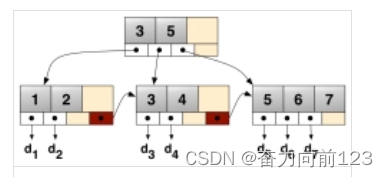
B+树是B树的一种变形形式，B+树上的叶子结点存储关键字以及相应记录的地址，叶子结点以上各层作为索引使用。一棵m阶的B+树定义如下:
(1)每个结点至多有m个子女；
(2)除根结点外，每个结点至少有[m/2]个子女，根结点至少有两个子女；
(3)有k个子女的结点必有k个关键字。
B+树的查找与B树不同，当索引部分某个结点的关键字与所查的关键字相等时，并不停止查找，应继续沿着这个关键字左边的指针向下，一直查到该关键字所在的叶子结点为止。

3、二叉树的遍历

遍历是对树的一种最基本的运算，所谓遍历二叉树，就是按一定的规则和顺序走遍二叉树的所有节点，使每一个节点都被访问一次，而且只被访问一次。由于二叉树是非线性结构，因此，树的遍历实质上是将二叉树的各个节点转换成为一个线性序列来表示

二叉树的三种遍历方式：

1、什么是先序遍历
先遍历根（父）节点、再遍历左节点、最后遍历右节点。

所以，先序遍历展开来讲是：如果一棵树上有根节点，则先输出根节点，再输出左孩子节点、最后输出右孩子节点。

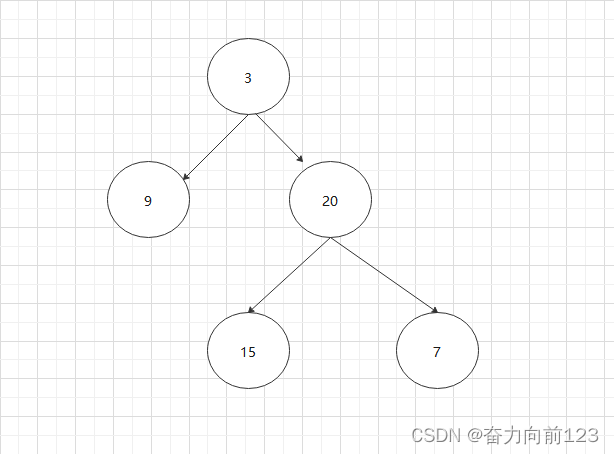
例如，上述图中的二叉树，先序遍历输出是：3、9、20、15、7

2、什么是中序遍历
先遍历输出左孩子节点，再遍历输出根节点，最后遍历输出右孩子节点。

例如，上述图中的二叉树，中序遍历输出是：9、3、15、20、7

3、什么是后序遍历
先遍历输出左孩子节点，再遍历输出右孩子节点，最后遍历输出根节点。

例如，上述图中的二叉树，后序遍历输出是：9、15、7、20、3

四、二叉树的实现

1、实体类：

@Data
public class TreeNode {

    /** 节点ID */
    private Integer id;

    /** 父节点ID：顶级节点为0 */
    private Integer parentId;

    /** 节点名称 */
    private String label;

    /** 子节点 */
    private List<TreeNode> children;
    /** 构造函数 */
    public TreeNode(Integer id, Integer parentId, String label) {
        this.id = id;
        this.parentId = parentId;
        this.label = label;
    }
}

2、实现类

@Service
public class TreeBuild {

    // 保存参与构建树形的所有数据（通常数据库查询结果）
    public List<TreeNode> nodeList = new ArrayList<>();

    /**
     *  构造方法
     *  @param nodeList 将数据集合赋值给nodeList，即所有数据作为所有节点。
     */
    public TreeBuild(List<TreeNode> nodeList){
        this.nodeList = nodeList;
    }

    /**
     *   获取需构建的所有根节点（顶级节点） "0"
     *   @return 所有根节点List集合
     */
    public List<TreeNode> getRootNode(){
        // 保存所有根节点（所有根节点的数据）
        List<TreeNode> rootNodeList = new ArrayList<>();
        // treeNode：查询出的每一条数据（节点）
        for (TreeNode treeNode : nodeList){
            // 判断当前节点是否为根节点，此处注意：若parentId类型是String，则要采用equals()方法判断。
            if (0 == treeNode.getParentId()) {
                // 是，添加
                rootNodeList.add(treeNode);
            }
        }
        return rootNodeList;
    }

    /**
     *  根据每一个顶级节点（根节点）进行构建树形结构
     *  @return  构建整棵树
     */
    public List<TreeNode> buildTree(){
        // treeNodes：保存一个顶级节点所构建出来的完整树形
        List<TreeNode> treeNodes = new ArrayList<TreeNode>();
        // getRootNode()：获取所有的根节点
        for (TreeNode treeRootNode : getRootNode()) {
            // 将顶级节点进行构建子树
            treeRootNode = buildChildTree(treeRootNode);
            // 完成一个顶级节点所构建的树形，增加进来
            treeNodes.add(treeRootNode);
        }
        return treeNodes;
    }

    /**
     *  递归-----构建子树形结构
     *  @param  pNode 根节点（顶级节点）
     *  @return 整棵树
     */
    public TreeNode buildChildTree(TreeNode pNode){ // 调用一次该方法就相当于给TreeNode对象添加children属性
        List<TreeNode> childTree = new ArrayList<TreeNode>();
        // nodeList：所有节点集合（所有数据）
        for (TreeNode treeNode : nodeList) {
            // 判断当前节点的父节点ID是否等于根节点的ID，即当前节点为其下的子节点
            if (treeNode.getParentId().equals(pNode.getId())) {
                // 再递归进行判断当前节点的情况，调用自身方法
                childTree.add(buildChildTree(treeNode));
            }
        }
        // for循环结束，即节点下没有任何节点，树形构建结束，设置树结果
        pNode.setChildren(childTree);
        return pNode;
    }
}