[PyTorch][chapter 61][强化学习-免模型学习1]

news2024/11/27 15:56:37

前言：

在现实的学习任务中，环境 $E=<X,A,P,R>$

其中的转移概率P,奖赏函数R 是未知的，或者状态X也是未知的

称为免模型学习（model-free learning）

1: 蒙特卡洛强化学习

2：同策略-蒙特卡洛强化学习

3：异策略- 蒙特卡洛强化学习

一蒙特卡洛强化学习

在免模型学习的情况下，策略迭代算法会遇到两个问题：

　　1: 是策略无法评估
因为无法做全概率展开。此时只能通过在环境中执行相应的动作观察得到的奖赏和转移的状态、

解决方案：一种直接的策略评估代替方法就是“采样”，然后求平均累积奖赏，作为期望累积奖赏的近似，这称为“蒙特卡罗强化学习”。

　　2: 策略迭代算法估计的是状态值函数（state value function） V，而最终的策略是通过状态动作值函数（state-action value function） Q 来获得。
模型已知时，有很简单的从 V 到 Q 的转换方法，而模型未知则会出现困难。

解决方案：所以我们将估计对象从 V 转为 Q，即：估计每一对 “状态-动作”的值函数。

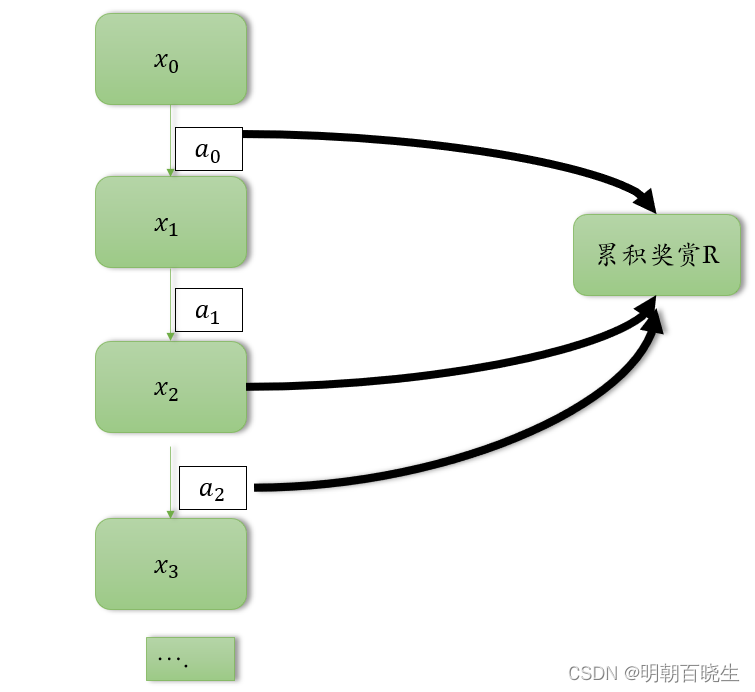
模型未知的情况下，我们从起始状态出发，使用某种策略进行采样，执行该策略T步，

并获得轨迹 $< x_0,a_0,r_1,a_1,r_2,...x_{T-1},a_{T-1},r_T,x_T>$ ,

然后对轨迹中出现的每一对 状态-动作,记录其后的奖赏之和,作为 状态-动作 对的一次

累积奖赏采样值. 多次采样得到多条轨迹后，将每个状态-动作对的累积奖赏采样值进行平均。即得到状态-动作值函数的估计.

二同策略蒙特卡洛强化学习

要获得好的V值函数估计,就需要不同的采样轨迹。

我们将确定性的策略 $\pi$ 称为原始策略

原始策略上使用 $\epsilon$ -贪心法的策略记为 $\pi^{\epsilon }(x)=$

以概率 $1-\epsilon$ 选择策略1: 策略1 ： $\pi(x)$

以概率 $\epsilon$ 选择策略2：策略2：均匀概率选取动作,

对于最大化值函数的原始策略

$\pi= argmax_{a}Q(x,a)$

其中 $\epsilon-$ 贪心策略 $\pi^{\epsilon }$ 中:

当前最优动作被选中的概率 $1-\epsilon +\frac{\epsilon }{|A|}$

每个非最优动作选中的概率 $\frac{\epsilon }{|A|}$ ，多次采样后将产生不同的采样轨迹。

因此对于最大值函数的原始策略 $\pi^{'}$ ,同样有

算法中，每采样一条轨迹，就根据该轨迹涉及的所有"状态-动作"对值函数进行更新

同策略蒙特卡罗强化学习算法最终产生的是E-贪心策略。然而，引入E-贪心策略是为了便于策略评估，而不是最终使用

三同策略蒙特卡洛算法 Python

# -*- coding: utf-8 -*-
"""
Created on Fri Nov  3 09:37:32 2023

@author: chengxf2
"""

# -*- coding: utf-8 -*-
"""
Created on Thu Nov  2 19:38:39 2023

@author: cxf
"""

import random
from enum import Enum

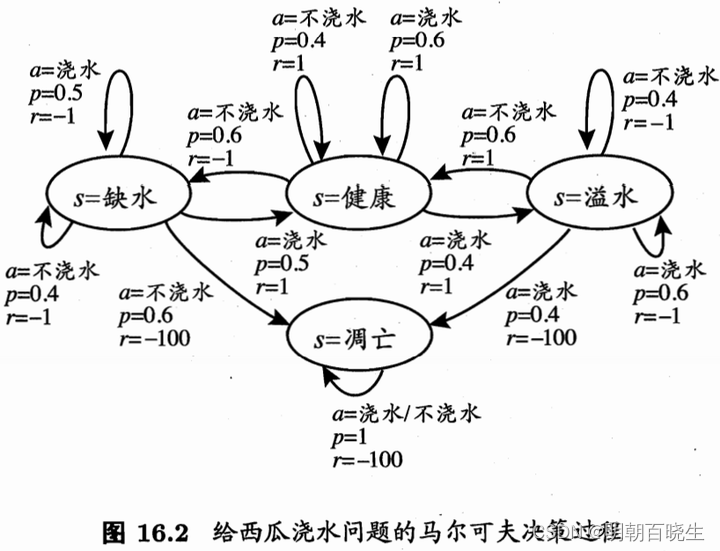
class State(Enum):
    '''状态空间X'''
    shortWater =1 #缺水
    health = 2   #健康
    overflow = 3 #溢水
    apoptosis = 4 #凋亡

class Action(Enum):
    '''动作空间A'''
    water = 1 #浇水
    noWater = 2 #不浇水
    
class Env():
    
    def reward(self, nextState):
        
        r = -100
        if nextState is State.shortWater:
             
            r =-1
            
        elif nextState is State.health:
            
            r = 1
            
        elif nextState is State.overflow:
            r= -1
        else:
            r = -100
        return r
            
    
    def action(self, state, action):
         
       
         if state is State.shortWater:
             #print("\n state--- ",state, "\t action---- ",action)
             if action is Action.water :
              
                 S =[State.shortWater, State.health]
                 proba =[0.5, 0.5]
             else:
                 S =[State.shortWater, State.apoptosis]
                 proba =[0.4, 0.6]
             
            
         elif state is State.health:
             #健康
             if action is Action.water :
                 S =[State.health, State.overflow]
                 proba =[0.6, 0.4]
             else:
                 S =[State.shortWater, State.health]
                 proba =[0.6, 0.4]
             
         elif state is State.overflow:
             #溢水
             if action is Action.water :
                 S =[State.overflow, State.apoptosis]
                 proba =[0.6, 0.4]
             else:
                 S =[State.health, State.overflow]
                 proba =[0.6, 0.4]
             
         else:  
             #凋亡
                 S =[State.apoptosis]
                 proba =[1.0]
         #print("\n S",S, "\t prob ",proba)
         nextState = random.choices(S, proba)[0]
         
         r = self.reward(nextState)
         #print("\n nextState ",nextState,"\t reward ",r)
         return nextState,r
         
         
         
     
    def __init__(self):
         
         self.X = None
         
    
     
    
    
    
class Agent():
    
    
    def initPolicy(self):
        
        self.Q ={}
        self.count ={}
        brandom = True #使用随机策略
        for state in self.S:
            for action in self.A:
                self. Q[state, action] = 0
                self.count[state,action]= 0
                randProb= [0.5,0.5]
                
        return self.Q, self.count, randProb,brandom
                
    
    def randomPolicy(self,randProb,T):
        
        A = self.A
        env = Env()
        state = State.shortWater #从缺水开始
        
        history =[]
        for t in range(T):
            a = random.choices(A, randProb)[0]
            nextState,r = env.action(state, a)
            item = [state,a,r,nextState]
            history.append(item)
            state = nextState
        
        return history
    
    def runPolicy(self,policy,T):
        

        env = Env()
        state = State.shortWater #从缺水开始
        
        history =[]
        for t in range(T):
            
            action = policy[state]
            nextState,r = env.action(state, action)
            item = [state,action,r,nextState]
            history.append(item)
            state = nextState
        
        return history
       
    def getTotalReward(self, t,T, history):
        
        denominator =T -t
        totalR = 0.0
        
        for i in range(t,T):#列表下标为0 开始，所以不需要t+1
            r= history[i][2]
            totalR +=r
            
        return totalR/denominator
              
    def updateQ(self, t ,history,R):
           #[state,action,r,nextState]
           state = history[t][0]
           action = history[t][1]
           count = self.count[state,action]
           
           self.Q[state, action]= (self.Q[state,action]*count+R)/(count+1)
           self.count[state,action] = count+1
           
           
        
        
        
    def learn(self):
        
        Q,count,randProb,bRandom =self.initPolicy()
        T =10
        policy ={}
        
        for s in range(1,self.maxIter): #采样第S 条轨迹
            
            if bRandom: #使用随机策略
                history = self.randomPolicy(randProb, T)
                #print(history)
            else:
              
                print("\n 迭代次数 %d"%s ,"\t 缺水：",policy[State.shortWater].name,
                                          "\t 健康：",policy[State.health].name,
                                         "\t 溢水：",policy[State.overflow].name,
                                         "\t 凋亡：",policy[State.apoptosis].name)
                history = self.runPolicy(policy, T)
                
            #已经有了一条轨迹了
            for t in range(0,T-1):
                R = self.getTotalReward(t, T, history)
                self.updateQ(t, history, R)
                
            rand = random.random()
            
            if rand < self.epsilon: #随机策略执行
                bRandom = True
            else:
                bRandom = False
                
                for state in self.S:
                    maxR = self.Q[state, self.A[0]]
                    for action in self.A:
                        
                        r = self.Q[state,action]

                        if r>=maxR:
                            policy[state] = action
                            maxR = r
        return policy
               
                        

                

    
    def __init__(self):
        
        self.S = [State.shortWater, State.health, State.overflow, State.apoptosis]
        self.A = [Action.water, Action.noWater]
        self.Q ={}
        self.count ={}
        self.policy ={}
        self.maxIter =5
        self.epsilon = 0.2


    
if  __name__ == "__main__":
    
     agent = Agent()
     agent.learn()

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1166829.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！