Those who do not remember the past are condemned to repeat it.

那些不能铭记历史的人注定要重蹈覆辙。

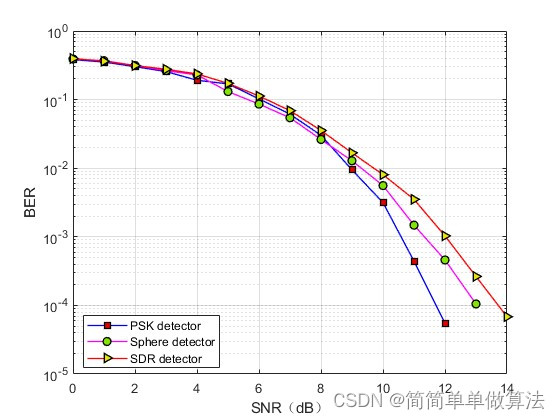
在动态规划——经典案例分析中我们提到了斐波那契数列的求解思路。知道动态规划的主要优点是能够在解决问题时避免重复计算，通过利用已经计算过的结果来加速求解过程。

斐波那契数列的递归操作是怎么完成的，使用动态规划帮我们节省了哪些重复的计算？
这些问题是本文所要研究和探讨的内容。

斐波那契数列是一个经典的数学问题，定义如下：

- F(0) = 0, F(1) = 1
- F(n) = F(n-1) + F(n-2)，其中 n > 1

如果采用递归进行求解的话，代码如下

long fib(int n){
	if (n==0) return 0;
	if (n==1) return 1;
	return fib(n-1) + fib(n-2);
}

此时算法的时间复杂度为 $F(n)=\Theta ({\varphi }^n)$，其中 $\varphi =\frac{\sqrt{5}+1}{2}\approx 1.618$

以 fib(7) 作为例子，分析它的的递归调用树

可以看到存在比较多的重复计算， 其中 fib(2) 重复计算了 8 次； fib(3)重复计算了 5 次。但我们没有必要重复计算 $F_k$ 的值如果已经计算出 $F_k$ 的值，不妨存储下来，下次需要的时候直接使用。可以形象地称中间计算结果的存储空间为 备忘录 。

---

#define UNKNOWN -1
std::vector<long> f;
long fib_m(int n) {
	if (f[n] == UNKNOWN)
		f[n] = fib_m(n - 1) + fib_m(n - 2);
	return f[n];
}

long fib_m_driver(int n) {
	f = std::vector<long>(n + 1，UNKNOWN);
	f[0] = 0; f[1] = 1;
	return fib_m(n);
}

通过引入 备忘录 空间 $f[n]$ ，我们可以将递归的很多重复计算支点消除。此时算法的时间复杂度为 $O(n)$ ;空间复杂度为 $O(n)$。

走到这一步其实还存在优化空间，对于每一个 fib(n) ，我们其实只需要知道 fib(n-1) 和 fib(n-2)的值，所以无需保存fib(0)至fib(n-3)的值。所以空间复杂度可以进一步减少到 $O(1)$

---

long fib_o(int n) {
	long prev = 1, curr = 0, next;
	for (int i = 1; i <= n; i++) {
		next = curr + prev;
		prev = curr;
		curr = next;
	}
	return curr;
}

这是自底向上的主动填充 备忘录 。这一步需要根据递归关系决定如何填充 备忘录 。通过自底向上填写 备忘录 ，我们消除了递归调用的时空开销。

---

小结

• 动机：在递归求解的过程中重复求解子问题
• 策略: 通过空间换时间，将子问题的解存储下来，避免重复计算
  • 空间: 子问题的数量
  • 子问题的数量由子问题的参数决定
    斐波那契数的子问题只有一个参数且O i< n
• 动态规划关键: 找到正确且高效的递归关系
• 求解方式
  1. 自顶向下: 被动填充备忘录，递归调用决定备忘录的填充顺序
  2. 自底向上: 主动填充备忘录，需要根据递归关系决定如何填充备忘录
     自底向上没有递归调用的时空开销

---