L1和L2正则化通俗理解

机器学习中，如果参数过多，模型过于复杂，容易造成过拟合（overfit）。即模型在训练样本数据上表现的很好，但在实际测试样本上表现的较差，不具备良好的泛化能力。为了避免过拟合，最常用的一种方法是使用使用正则化，例如 L1 和 L2 正则化。

1. L1和L2的区别

在机器学习中，

L1范数(L2 normalization)是指向量中各个元素绝对值之和，通常表述为 $\|\boldsymbol{w_i}\|_1$ ，线性回归中使用L1正则的模型也叫Lasso regularization
比如向量A=[1，-1，3]，那么A的L1范数为 |1|+|-1|+|3|.

L2范数指权值向量w中各个元素的平方和然后再求平方根（可以看到Ridge回归的L2正则化项有平方符号），通常表示为 $\|\boldsymbol{w_i}\|_2$ ，线性回归中使用L2正则的模型又叫岭回归(Ringe regularization)。

简单总结一下就是：

L1范数: 为x向量各个元素绝对值之和。
L2范数: 为x向量各个元素平方和的1/2次方，L2范数又称Euclidean范数或者Frobenius范数
Lp范数: 为x向量各个元素绝对值p次方和的1/p次方.
下图为p从无穷到0变化时，三维空间中到原点的距离（范数）为1的点构成的图形的变化情况。以常见的L-2范数（p=2）为例，此时的范数也即欧氏距离，空间中到原点的欧氏距离为1的点构成了一个球面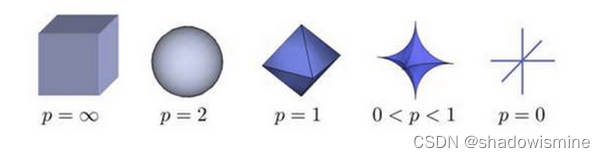

参数正则化作用

L1： 为模型加入先验，简化模型，使权值稀疏，由于权值的稀疏，从而过滤掉一些无用特征，防止过拟合
L2： 根据L2的特性，它会使得权值减小，即使平滑权值，一定程度上也能和L1一样起到简化模型，加速训练的作用，同时可防止模型过拟合

2. L2 正则化直观解释

L2 正则化公式非常简单，直接在原来的损失函数基础上加上权重参数的平方和：

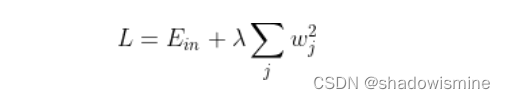
其中，Ein 是未包含正则化项的训练样本误差，λ 是正则化参数，可调。但是正则化项是如何推导的？接下来，我将详细介绍其中的物理意义。

我们知道，正则化的目的是限制参数过多或者过大，避免模型更加复杂。例如，使用多项式模型，如果使用 10 阶多项式，模型可能过于复杂，容易发生过拟合。所以，为了防止过拟合，我们可以将其高阶部分的权重 w 限制为 0，这样，就相当于从高阶的形式转换为低阶。

为了达到这一目的，最直观的方法就是限制 w 的个数，但是这类条件属于 NP-hard 问题，求解非常困难。所以，一般的做法是寻找更宽松的限定条件：

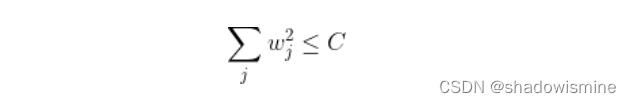
上式是对 w 的平方和做数值上界限定，即所有w 的平方和不超过参数 C。这时候，我们的目标就转换为：最小化训练样本误差 Ein，但是要遵循 w 平方和小于 C 的条件。

下面，我用一张图来说明如何在限定条件下，对 Ein 进行最小化的优化。

如上图所示，蓝色椭圆区域是最小化 Ein 区域，红色圆圈是 w 的限定条件区域。在没有限定条件的情况下，一般使用梯度下降算法，在蓝色椭圆区域内会一直沿着 w 梯度的反方向前进，直到找到全局最优值 wlin。例如空间中有一点 w（图中紫色点），此时 w 会沿着 -∇Ein 的方向移动，如图中蓝色箭头所示。但是，由于存在限定条件，w 不能离开红色圆形区域，最多只能位于圆上边缘位置，沿着切线方向。w 的方向如图中红色箭头所示。

那么问题来了，存在限定条件，w 最终会在什么位置取得最优解呢？也就是说在满足限定条件的基础上，尽量让 Ein 最小。

我们来看，w 是沿着圆的切线方向运动，如上图绿色箭头所示。运动方向与 w 的方向（红色箭头方向）垂直。运动过程中，根据向量知识，只要 -∇Ein 与运行方向有夹角，不垂直，则表明 -∇Ein 仍会在 w 切线方向上产生分量，那么 w 就会继续运动，寻找下一步最优解。只有当 -∇Ein 与 w 的切线方向垂直时，-∇Ein在 w 的切线方向才没有分量，这时候 w 才会停止更新，到达最接近 wlin 的位置，且同时满足限定条件。

-∇Ein 与 w 的切线方向垂直，即 -∇Ein 与 w 的方向平行。如上图所示，蓝色箭头和红色箭头互相平行。这样，根据平行关系得到：

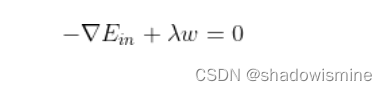
移项，得：

这样，我们就把优化目标和限定条件整合在一个式子中了。也就是说只要在优化 Ein 的过程中满足上式，就能实现正则化目标。

接下来，重点来了！根据最优化算法的思想：梯度为 0 的时候，函数取得最优值。已知 ∇Ein 是 Ein 的梯度，观察上式，λw 是否也能看成是某个表达式的梯度呢？

当然可以！λw 可以看成是 1/2λw*w 的梯度：

这样，我们根据平行关系求得的公式，构造一个新的损失函数：

之所以这样定义，是因为对 Eaug 求导，正好得到上面所求的平行关系式。上式中等式右边第二项就是 L2 正则化项。

这样，我们从图像化的角度，分析了 L2 正则化的物理意义，解释了带 L2 正则化项的损失函数是如何推导而来的。

3. L1 正则化直观解释

L1 正则化公式也很简单，直接在原来的损失函数基础上加上权重参数的绝对值：

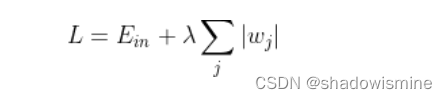
我仍然用一张图来说明如何在 L1 正则化下，对 Ein 进行最小化的优化。

Ein 优化算法不变，L1 正则化限定了 w 的有效区域是一个正方形，且满足 |w| < C。空间中的点 w 沿着 -∇Ein 的方向移动。但是，w 不能离开红色正方形区域，最多只能位于正方形边缘位置。其推导过程与 L2 类似，此处不再赘述。

4. L1 与 L2 解的稀疏性

介绍完 L1 和 L2 正则化的物理解释和数学推导之后，我们再来看看它们解的分布性。

以二维情况讨论，上图左边是 L2 正则化，右边是 L1 正则化。从另一个方面来看，满足正则化条件，实际上是求解蓝色区域与黄色区域的交点，即同时满足限定条件和 Ein 最小化。对于 L2 来说，限定区域是圆，这样，得到的解 w1 或 w2 为 0 的概率很小，很大概率是非零的。

对于 L1 来说，限定区域是正方形，方形与蓝色区域相交的交点是顶点的概率很大，这从视觉和常识上来看是很容易理解的。也就是说，方形的凸点会更接近 Ein 最优解对应的 wlin 位置，而凸点处必有 w1 或 w2 为 0。这样，得到的解 w1 或 w2 为零的概率就很大了。所以，L1 正则化的解具有稀疏性。

扩展到高维，同样的道理，L2 的限定区域是平滑的，与中心点等距；而 L1 的限定区域是包含凸点的，尖锐的。这些凸点更接近 Ein 的最优解位置，而在这些凸点上，很多 wj 为 0。

另外通过公式也能更好的理解为什么L1具备稀疏性。

假设只有一个参数为w，损失函数为L ( w )，分别加上L1正则项和L2正则项后有：

假设L ( w )在0处的导数为d0，即

则可以推导使用L1正则和L2正则时的导数。

引入L2正则项，在0处的导数

引入L1正则项，在0处的导数

可见，引入L2正则时，代价函数在0处的导数仍是d0，无变化。而引入L1正则后，代价函数在0处的导数有一个突变。从d0 + λ 到d0 − λ，若d0 + λ 和d0 − λ 异号，则在0处会是一个极小值点。因此，优化时，很可能优化到该极小值点上，即w = 0处。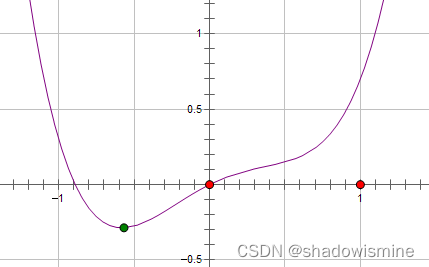

5. 正则化参数 λ

正则化是结构风险最小化的一种策略实现，能够有效降低过拟合。损失函数实际上包含了两个方面：一个是训练样本误差。一个是正则化项。其中，参数 λ 起到了权衡的作用。

以 L2 为例，若 λ 很小，对应上文中的 C 值就很大。这时候，圆形区域很大，能够让 w 更接近 Ein 最优解的位置。若 λ 近似为 0，相当于圆形区域覆盖了最优解位置，这时候，正则化失效，容易造成过拟合。相反，若 λ 很大，对应上文中的 C 值就很小。这时候，圆形区域很小，w 离 Ein 最优解的位置较远。w 被限制在一个很小的区域内变化，w 普遍较小且接近 0，起到了正则化的效果。但是，λ 过大容易造成欠拟合。欠拟合和过拟合是两种对立的状态。

6. pytorch实现L1与L2正则化

网上很多关于L2和L1正则化的对象都是针对参数的，或者说权重，即权重衰减，可以用pytorch很简单的实现L2惩罚：

class torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)

如上，weight_decay参数即为L2惩罚项前的系数

举个栗子，对模型中的某些参数进行惩罚时

#定义一层感知机
net = nn.Linear(num_inputs, 1)
#自定义参数初始化
nn.init.normal_(net.weight, mean=0, std=1)
nn.init.normal_(net.bias, mean=0, std=1)
optimizer_w = torch.optim.SGD(params=[net.weight], lr=lr, weight_decay=wd) # 对权重参数衰减，惩罚项前的系数为wd
optimizer_b = torch.optim.SGD(params=[net.bias], lr=lr)  # 不对偏差参数衰减

而对于L1正则化或者其他的就比较麻烦了，因为pytorch优化器只封装了L2惩罚功能，需要自定义L1方法：

class Regularization(torch.nn.Module):
    def __init__(self,model,weight_decay,p=2):
        '''
        :param model 模型
        :param weight_decay:正则化参数
        :param p: 范数计算中的幂指数值，默认求2范数,
                  当p=0为L2正则化,p=1为L1正则化
        '''
        super(Regularization, self).__init__()
        if weight_decay <= 0:
            print("param weight_decay can not <=0")
            exit(0)
        self.model=model
        self.weight_decay=weight_decay
        self.p=p
        self.weight_list=self.get_weight(model)
        self.weight_info(self.weight_list)
 
    def to(self,device):
        '''
        指定运行模式
        :param device: cude or cpu
        :return:
        '''
        self.device=device
        super().to(device)
        return self
 
    def forward(self, model):
        self.weight_list=self.get_weight(model)#获得最新的权重
        reg_loss = self.regularization_loss(self.weight_list, self.weight_decay, p=self.p)
        return reg_loss
 
    def get_weight(self,model):
        '''
        获得模型的权重列表
        :param model:
        :return:
        '''
        weight_list = []
        for name, param in model.named_parameters():
            if 'weight' in name:
                weight = (name, param)
                weight_list.append(weight)
        return weight_list
 
    def regularization_loss(self,weight_list, weight_decay, p=2):
        '''
        计算张量范数
        :param weight_list:
        :param p: 范数计算中的幂指数值，默认求2范数
        :param weight_decay:
        :return:
        '''
        # weight_decay=Variable(torch.FloatTensor([weight_decay]).to(self.device),requires_grad=True)
        # reg_loss=Variable(torch.FloatTensor([0.]).to(self.device),requires_grad=True)
        # weight_decay=torch.FloatTensor([weight_decay]).to(self.device)
        # reg_loss=torch.FloatTensor([0.]).to(self.device)
        reg_loss=0
        for name, w in weight_list:
            l2_reg = torch.norm(w, p=p)
            reg_loss = reg_loss + l2_reg
 
        reg_loss=weight_decay*reg_loss
        return reg_loss
 
    def weight_info(self,weight_list):
        '''
        打印权重列表信息
        :param weight_list:
        :return:
        '''
        print("---------------regularization weight---------------")
        for name ,w in weight_list:
            print(name)
        print("---------------------------------------------------")

class Regularization的使用


# 检查GPU是否可用
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
 
print("-----device:{}".format(device))
print("-----Pytorch version:{}".format(torch.__version__))
 
weight_decay=100.0 # 正则化参数
 
model = my_net().to(device)
# 初始化正则化
if weight_decay>0:
   reg_loss=Regularization(model, weight_decay, p=2).to(device)
else:
   print("no regularization")
 
 
criterion= nn.CrossEntropyLoss().to(device) # CrossEntropyLoss=softmax+cross entropy
optimizer = optim.Adam(model.parameters(),lr=learning_rate)#不需要指定参数weight_decay
 
# train
batch_train_data=...
batch_train_label=...
 
out = model(batch_train_data)
 
# loss and regularization
loss = criterion(input=out, target=batch_train_label)
if weight_decay > 0:
   loss = loss + reg_loss(model)
total_loss = loss.item()
 
# backprop
optimizer.zero_grad()#清除当前所有的累积梯度
total_loss.backward()
optimizer.step()

7. 如何判断正则化作用了模型？

一般来说，正则化的主要作用是避免模型产生过拟合，当然啦，过拟合问题，有时候是难以判断的。但是，要判断正则化是否作用了模型，还是很容易的。下面我给出两组训练时产生的loss和Accuracy的log信息，一组是未加入正则化的，一组是加入正则化：

7.1 未加入正则化loss和Accuracy

优化器采用Adam，并且设置参数weight_decay=0.0，即无正则化的方法

optimizer = optim.Adam(model.parameters(),lr=learning_rate,weight_decay=0.0)

训练时输出的 loss和Accuracy信息

step/epoch:0/0,Train Loss: 2.418065, Acc: [0.15625]
step/epoch:10/0,Train Loss: 5.194936, Acc: [0.34375]
step/epoch:20/0,Train Loss: 0.973226, Acc: [0.8125]
step/epoch:30/0,Train Loss: 1.215165, Acc: [0.65625]
step/epoch:40/0,Train Loss: 1.808068, Acc: [0.65625]
step/epoch:50/0,Train Loss: 1.661446, Acc: [0.625]
step/epoch:60/0,Train Loss: 1.552345, Acc: [0.6875]
step/epoch:70/0,Train Loss: 1.052912, Acc: [0.71875]
step/epoch:80/0,Train Loss: 0.910738, Acc: [0.75]
step/epoch:90/0,Train Loss: 1.142454, Acc: [0.6875]
step/epoch:100/0,Train Loss: 0.546968, Acc: [0.84375]
step/epoch:110/0,Train Loss: 0.415631, Acc: [0.9375]
step/epoch:120/0,Train Loss: 0.533164, Acc: [0.78125]
step/epoch:130/0,Train Loss: 0.956079, Acc: [0.6875]
step/epoch:140/0,Train Loss: 0.711397, Acc: [0.8125]

7.2 加入正则化loss和Accuracy

优化器采用Adam，并且设置参数weight_decay=10.0，即正则化的权重lambda =10.0

optimizer = optim.Adam(model.parameters(),lr=learning_rate,weight_decay=10.0)

这时，训练时输出的 loss和Accuracy信息：

step/epoch:0/0,Train Loss: 2.467985, Acc: [0.09375]
step/epoch:10/0,Train Loss: 5.435320, Acc: [0.40625]
step/epoch:20/0,Train Loss: 1.395482, Acc: [0.625]
step/epoch:30/0,Train Loss: 1.128281, Acc: [0.6875]
step/epoch:40/0,Train Loss: 1.135289, Acc: [0.6875]
step/epoch:50/0,Train Loss: 1.455040, Acc: [0.5625]
step/epoch:60/0,Train Loss: 1.023273, Acc: [0.65625]
step/epoch:70/0,Train Loss: 0.855008, Acc: [0.65625]
step/epoch:80/0,Train Loss: 1.006449, Acc: [0.71875]
step/epoch:90/0,Train Loss: 0.939148, Acc: [0.625]
step/epoch:100/0,Train Loss: 0.851593, Acc: [0.6875]
step/epoch:110/0,Train Loss: 1.093970, Acc: [0.59375]
step/epoch:120/0,Train Loss: 1.699520, Acc: [0.625]
step/epoch:130/0,Train Loss: 0.861444, Acc: [0.75]
step/epoch:140/0,Train Loss: 0.927656, Acc: [0.625]

当weight_decay=10000.0

step/epoch:0/0,Train Loss: 2.337354, Acc: [0.15625]
step/epoch:10/0,Train Loss: 2.222203, Acc: [0.125]
step/epoch:20/0,Train Loss: 2.184257, Acc: [0.3125]
step/epoch:30/0,Train Loss: 2.116977, Acc: [0.5]
step/epoch:40/0,Train Loss: 2.168895, Acc: [0.375]
step/epoch:50/0,Train Loss: 2.221143, Acc: [0.1875]
step/epoch:60/0,Train Loss: 2.189801, Acc: [0.25]
step/epoch:70/0,Train Loss: 2.209837, Acc: [0.125]
step/epoch:80/0,Train Loss: 2.202038, Acc: [0.34375]
step/epoch:90/0,Train Loss: 2.192546, Acc: [0.25]
step/epoch:100/0,Train Loss: 2.215488, Acc: [0.25]
step/epoch:110/0,Train Loss: 2.169323, Acc: [0.15625]
step/epoch:120/0,Train Loss: 2.166457, Acc: [0.3125]
step/epoch:130/0,Train Loss: 2.144773, Acc: [0.40625]
step/epoch:140/0,Train Loss: 2.173397, Acc: [0.28125]

7.3 正则化说明

就整体而言，对比加入正则化和未加入正则化的模型，训练输出的loss和Accuracy信息，我们可以发现，加入正则化后，loss下降的速度会变慢，准确率Accuracy的上升速度会变慢，并且未加入正则化模型的loss和Accuracy的浮动比较大（或者方差比较大），而加入正则化的模型训练loss和Accuracy，表现的比较平滑。并且随着正则化的权重lambda越大，表现的更加平滑。这其实就是正则化的对模型的惩罚作用，通过正则化可以使得模型表现的更加平滑，即通过正则化可以有效解决模型过拟合的问题。

8. 特征正则化

上面介绍了对于权重进行正则化的作用以及具体实现，其实在很多模型中，也会对特征采用L2归一化，有的时候在训练模型时，经过几个batch后，loss会变成nan，此时，如果你在特征后面加上L2归一化，可能可以很好的解决这个问题，而且有时会影响训练的效果，深有体会。
L2正则的原理比较简单，如下公式：

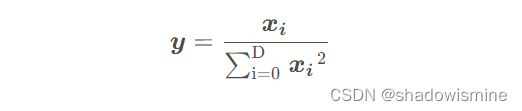
其中D为向量的长度，经过l2正则后xi 向量的元素平方和等于1

python实现

def l2norm(X, dim=-1, eps=1e-12):
    """L2-normalize columns of X
    """
    norm = torch.pow(X, 2).sum(dim=dim, keepdim=True).sqrt() + eps
    X = torch.div(X, norm)
    return X

在SSD目标检测的conv4_3层便使用了L2Norm

对特征进行L2正则的具体作用如下：