基于OR-Tools的装箱问题模型求解（PythonAPI）

装箱问题

一、背包问题（Knapsack problem）
- 1.1 0-1背包模型
- - 基于OR-Tools的0-1背包问题求解（PythonAPI）
  - - 导入pywraplp库
    - 数据准备
    - 声明MIP求解器
    - 初始化决策变量
    - 初始化约束条件
    - 目标函数
    - 调用求解器
    - 打印结果
- 1.2 多重背包问题（Multiple knapsack problems）
- - 基于OR-Tools多重背包问题求解（PythonAPI）
- 1.3 多维背包问题（Multi-dimensional knapsack problems）
- - 基于OR-Tools多维背包问题求解（PythonAPI）
二、装箱问题（Bin-packing problem）
- - 基于OR-Tools的装箱问题求解（PythonAPI）

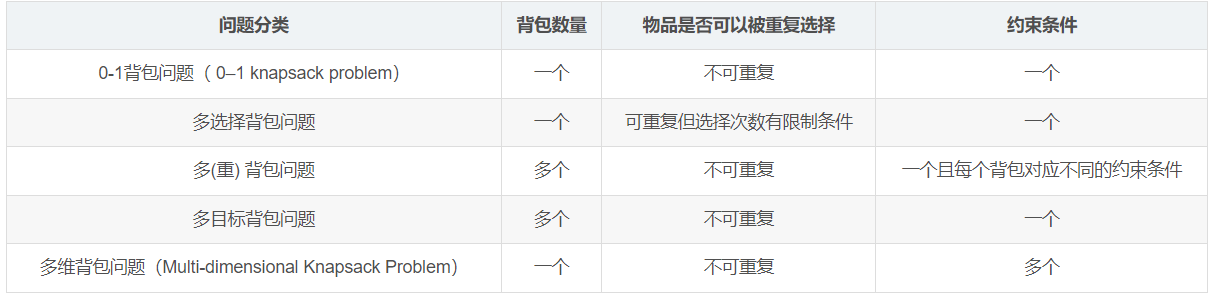
装箱问题（packing problem）的描述是要将一组给定尺寸的物品放置到具有固定容量的容器中，一般情况下由于容器有容量限制，不可能放入所有物品，那么装箱问题的目标是要找到限定约束下使得总价值最大或总花费最小的装箱方法。根据我们具体的目标情况，装箱问题又可分为两类：

背包问题(Knapsack problem)，容器数量是固定的，每个容器有自己的最大容量，而需要分配的物件有各自的价值，我们的目标是让装入容器的物体的总价值最大，并不要求所有物体都装入；
装箱问题（ Bin-packing problem），容器容量是相同的，但是数量不固定，我们的目标是用最少的容器来存放所有的物件。

一、背包问题（Knapsack problem）

旅行者要在一个背包内装入一些对旅行最有用得物品（旅行者对每件物品的价值都有评判）。背包最多只能装入总重为b单位的物品，并且对于每件物品只能选择整个携带或者不携带。假设共有n件物品，第 $j$ 件物品重 $a_j$ 单位，其价值为 $c_j$ 。在携带物品总重量不超过 $b$ 单位的条件下，请问如何装入物品以使背包内的物品价值最大?

1.1 0-1背包模型

对于 $j = 1, ..., n$ ，定义0-1决策变量 $x_j=1$ 表示携带物品 $j$ 。则物品的数学模型为：
$\begin{align} \max \quad &\sum_{j \in J} c_{j}x_{j} \\ \text{subject to} \quad &\sum_{j=1}^n a_{j}x_{j} \leq b, \\ &x_{j} \in \{0,1\}, \quad \forall j=1,...,n \end{align}$
具有上述形式的整数规划模型称为背包模型，其中约束条件（2）称为背包约束，约束条件（3）定义了0-1变量 $x_j$ 。

基于OR-Tools的0-1背包问题求解（PythonAPI）

OR-Tools官网题目
50个物品被装入一个箱子。每个物品都有一个值(物品上的数字)和一个重量(与物品的面积大致成比例)。背包的容量被为850，目标是找到一组能使总价值最大化而又不超过容量的物品。

导入pywraplp库

from ortools.linear_solver import pywraplp

数据准备

values = [
    360, 83, 59, 130, 431, 67, 230, 52, 93, 125, 670, 892, 600, 38, 48, 147,
    78, 256, 63, 17, 120, 164, 432, 35, 92, 110, 22, 42, 50, 323, 514, 28,
    87, 73, 78, 15, 26, 78, 210, 36, 85, 189, 274, 43, 33, 10, 19, 389, 276,
    312
]
weights = [
    7, 0, 30, 22, 80, 94, 11, 81, 70, 64, 59, 18, 0, 36, 3, 8, 15, 42, 9, 0,
    42, 47, 52, 32, 26, 48, 55, 6, 29, 84, 2, 4, 18, 56, 7, 29, 93, 44, 71,
    3, 86, 66, 31, 65, 0, 79, 20, 65, 52, 13
]
capacities = 850         # 背包容量
num_items = len(weights) # 物品数量

声明MIP求解器

solver = pywraplp.Solver.CreateSolver("SCIP")

初始化决策变量

x = {}
for j in range(num_items):
    x[j] = solver.IntVar(0, 1, f"x{j}")
print(x)

{0: x0, 1: x1, 2: x2, 3: x3, 4: x4, 5: x5, 6: x6, 7: x7, 8: x8, 9: x9, 10: x10, 11: x11, 12: x12, 13: x13, 14: x14, 15: x15, 16: x16, 17: x17, 18: x18, 19: x19, 20: x20, 21: x21, 22: x22, 23: x23, 24: x24, 25: x25, 26: x26, 27: x27, 28: x28, 29: x29, 30: x30, 31: x31, 32: x32, 33: x33, 34: x34, 35: x35, 36: x36, 37: x37, 38: x38, 39: x39, 40: x40, 41: x41, 42: x42, 43: x43, 44: x44, 45: x45, 46: x46, 47: x47, 48: x48, 49: x49}

初始化约束条件

solver.Add(solver.Sum([weights[j] * x[j] for j in range(num_items)]) <= capacities)

<ortools.linear_solver.pywraplp.Constraint; proxy of <Swig Object of type 'operations_research::MPConstraint *' at 0x0000017B2B458510> >

上面这种写法将列表推导式打开，等价于：

cn_terms = []
for j in range(num_items):
    cn_terms.append(weights[j] * x[j])
solver.Add(solver.Sum(cn_terms))

还有另外一种写法：

constraint = solver.RowConstraint(0, capacities, "")
for j in range(num_items):
    constraint.SetCoefficient(x[j], weights[j])

目标函数

objective_terms = []
for j in range(num_items):
    objective_terms.append(values[j] * x[j])
solver.Maximize(solver.Sum(objective_terms))

调用求解器

status = solver.Solve()

打印结果

if status == pywraplp.Solver.OPTIMAL or status == pywraplp.Solver.FEASIBLE:
    print(f"Total cost = {solver.Objective().Value()}")
    total_weight = 0
    picked_items = []
    for j in range(num_items):
        # Test if x[i,j] is 1 (with tolerance for floating point arithmetic).
        if x[j].solution_value() > 0.5:
            total_weight += weights[j]
            picked_items.append(j)
    print(f"total weight={total_weight}")
    print(f"装入了背包的物品：{picked_items}")

else:
    print("No solution found.")

Total cost = 7534.0
total weight=850
装入了背包的物品：[0, 1, 3, 4, 6, 10, 11, 12, 14, 15, 16, 17, 18, 19, 21, 22, 24, 27, 28, 29, 30, 31, 32, 34, 38, 39, 41, 42, 44, 47, 48, 49]

1.2 多重背包问题（Multiple knapsack problems）

把单个背包扩展到多个背包，就是多背包问题，对于多背包问题，我们可以采用下面的定义方式：
给出n个物件（j=1,…,n）和m个背包（i=1,…,m）(m ≤ n )，0-1决策变量x_ij =1将物品 j 装入背包 i 。按如下定义（仍然只是单维）：
$\begin{align} \max \quad & \sum_{i \in I}{}\sum_{j \in J} c_{j}x_{ij}\\ \text{subject to} \quad &\sum_{j=1}^n a_{j}x_{ij} \leq b_i, \quad \forall i =1,...,m \\ &\sum_{i \in I}{x_{ij}} \leq1,\quad \forall j =1,...,n \\ &x_{j} \in \{0,1\}, \quad \forall j=1,...,n \end{align}$

基于OR-Tools多重背包问题求解（PythonAPI）

# The problem is to pack a subset of the items into five bins, each of which has a maximum capacity of 100, so that the total packed value is a maximum.
# 导入pywraplp库
from ortools.linear_solver import pywraplp

weights = [48, 30, 42, 36, 36, 48, 42, 42, 36, 24, 30, 30, 42, 36, 36]
values = [10, 30, 25, 50, 35, 30, 15, 40, 30, 35, 45, 10, 20, 30, 25]
knapsack_capacities = [100, 100, 100, 100, 100]  # 5个背包的容量

num_items = len(weights)  # 物品数量
num_knapsacks = len(knapsack_capacities)  # 5个背包

# 声明MIP求解器
solver = pywraplp.Solver.CreateSolver("SCIP")

# 初始化决策变量
x = {}
for i in range(num_knapsacks):
    for j in range(num_items):
        x[i, j] = solver.IntVar(0, 1, f'x{i}{j}')

# 背包约束
for i in range(num_knapsacks):
    cn_terms = []
    for j in range(num_items):
        cn_terms.append(weights[j] * x[i, j])
    solver.Add(solver.Sum(cn_terms) <= knapsack_capacities[i])

# 约束：每个物品只能装入一个背包
for j in range(num_items):
    cn_terms = []
    for i in range(num_knapsacks):
        cn_terms.append(x[i, j])
    solver.Add(solver.Sum(cn_terms) <= 1)
# 目标函数
objective_terms = []
for i in range(num_knapsacks):
    for j in range(num_items):
        objective_terms.append(values[j] * x[i, j])
solver.Maximize(solver.Sum(objective_terms))
# 调用求解器
status = solver.Solve()
# 打印结果
if status == pywraplp.Solver.OPTIMAL or status == pywraplp.Solver.FEASIBLE:
    print(f"Total cost = {solver.Objective().Value()}\n")
    knapsack = {}
    for i in range(num_knapsacks):
        knapsack[i] = []
        for j in range(num_items):
            if x[i, j].solution_value() > .5:
                knapsack[i].append(j)
    print("背包—放入的物品：", knapsack)

1.3 多维背包问题（Multi-dimensional knapsack problems）

实际生活中可能限制背包存放物体数量的不仅是重量，还有体积等属性，因此上面的定义更严格的来说应该是单维单背包问题，如果有多维限定，那么在每一维存放物体的总量都不能超过背包的限定值。

$\begin{align} \max \quad & \sum_{i \in I}{}\sum_{j \in J} c_{j}x_{j}\\ \text{subject to} \quad &\sum_{j=1}^n a_{ij}x_{j} \leq b_i, \quad \forall i =1,...,m \\ &x_{j} \in \{0,1\}, \quad \forall j=1,...,n \end{align}$

决策变量 $x_j=1$ 代表物品 $j$ 装入背包；
$c_i$ ：物品 $i$ 的价值；
n：物品的个数；
$b_i$ 维度 $i$ 的背包约束，如重量、体积等；
$a_{ij}$ 表示物品 $j$ 对背包的约束 $i$ 的消耗；

基于OR-Tools多维背包问题求解（PythonAPI）

import pandas as pd
import numpy as np

# ==========测试==========
knapsack = {"weight": 600, "volume": 600}
values = [1898, 440, 22507, 270, 14148, 3100, 4650, 30800, 615, 4975, 1160, 4225, 510, 11880, 479, 440, 490, 330, 110,
          560, 24355, 2885, 11748, 4550, 750, 3720, 1950, 10500]

weights = [45, 5, 85, 150, 65, 95, 30, 12, 170, 20, 40, 25, 20, 3, 7, 25, 12, 22, 25, 9, 165, 2, 85, 15, 9, 2, 4, 100]
volumes = [30, 20, 125, 5, 80, 25, 35, 73, 12, 15, 15, 40, 5, 10, 10, 12, 10, 9, 10, 20, 60, 40, 50, 36, 49, 40, 19,
           150]
dimension_items = {
    "weight": weights,
    "volume": volumes
}
from ortools.linear_solver import pywraplp

solver = pywraplp.Solver.CreateSolver("SCIP")

num_dimensions = len(dimension_items)
num_items = len(values)
# 0-1决策变量
x = {}
for j in range(num_items):
    x[j] = solver.IntVar(0, 1, f'x{j}')

# 约束
for i in dimension_items.keys():
    cn_terms = []
    for j in range(num_items):
        cn_terms.append(dimension_items[i][j] * x[j])
    solver.Add(solver.Sum(cn_terms) <= knapsack[i])

# 目标函数
obj_terms = []
for j in range(num_items):
    obj_terms.append(values[j] * x[j])
solver.Maximize(solver.Sum(obj_terms))

status = solver.Solve()

if status == pywraplp.Solver.OPTIMAL or status == pywraplp.Solver.FEASIBLE:
    print(f"Total cost = {solver.Objective().Value()}\n")
    knapsack = []
    for j in range(num_items):
        if x[j].solution_value() > .5:
            knapsack.append(j)
    print("背包—放入的物品：", knapsack)

二、装箱问题（Bin-packing problem）

和背包问题不同，装箱问题问题是站在容器优化的角度来定义的，不再考虑放置物品的价值，而是希望用最少的容器装下所有的物品，每个容器的容量相同。装箱问题问题相比背包问题更加一般化，生活中物流等领域也常会遇到这种问题，比如用最少的运输车辆递送快递以最小化成本。

Bin packing problem: Given as many bins with a common capacity as necessary, find the fewest that will hold all the items. In this problem, the items aren’t assigned values, because the objective doesn’t involve value.

装箱问题问题也可以用整数规划模型来表示：
https://blog.csdn.net/wangzhenyang2/article/details/104595159

$\begin{align} \min \quad & \sum_{i}^m{} y_i\\ \text{subject to} \quad &\sum_{j=1}^n a_{j}x_{ij} \leq b \cdot y_i, \quad \forall i =1,...,m \\ &\sum_{i=1}^m x_{ij} = 1, \quad \forall j =1,...,m \\ &x_{j} \in \{0,1\}, \quad \forall j=1,...,n\\ &y_{i} \in \{0,1\}, \quad \forall i=1,...,m \end{align}$

决策变量 $x_{ij}=1$ 代表物品 $j$ 装入箱子 $i$ ；
决策变量 $y_{i}=1$ 代表箱子 $i$ 被使用；
$c_i$ ：物品 $i$ 的价值；
$n$ ：物品的个数；
$m$ ：箱子个数；
$b_i$ 维度 $i$ 的背包约束；
$a_{j}$ 表示物品 $j$ 的重量；

基于OR-Tools的装箱问题求解（PythonAPI）

在这个例子中，不同重量的物品需要装入到一组容量相同的箱子中。假设有足够的箱子可以装下所有的物品，目标为使用的箱子数量最小。

from ortools.linear_solver import pywraplp

weights = [48, 30, 19, 36, 36, 27, 42, 42, 36, 24, 30]  # a
num_items = len(weights)  # n
num_bins = num_items  # m
bin_capacity = 100  # b

solver = pywraplp.Solver.CreateSolver("SCIP")

# 初始化决策变量
# Variables
# x[i, j] = 1 if item i is packed in bin j.
x = {}
for i in range(num_bins):
    for j in range(num_items):
        x[(i, j)] = solver.IntVar(0, 1, "x_%i_%i" % (i, j))

# y[j] = 1 if bin j is used.
y = {}
for i in range(num_bins):
    y[i] = solver.IntVar(0, 1, "y[%i]" % i)

# 约束条件
for i in range(num_bins):
    cn_terms = []
    for j in range(num_items):
        cn_terms.append(weights[j] * x[i, j])
    solver.Add(solver.Sum(cn_terms) <= bin_capacity * y[i])

for j in range(num_items):
    cn_terms = []
    for i in range(num_bins):
        cn_terms.append(x[i, j])
    solver.Add(solver.Sum(cn_terms) == 1)

# 目标函数
obj_terms = []
for i in range(num_bins):
    obj_terms.append(y[i])
solver.Minimize(solver.Sum(obj_terms))

status = solver.Solve()

if status == pywraplp.Solver.OPTIMAL or status == pywraplp.Solver.FEASIBLE:
    print(f"num of bins = {solver.Objective().Value()}\n")

    for i in range(num_bins):
        bin = []
        if y[i].solution_value() == 1:
            for j in range(num_items):
                if x[i, j].solution_value() > .5:
                    bin.append(j)
            print(f'箱子{i}-装入物品：{bin}')
else:
    print("No solution found.")

num of bins = 4.0

箱子0-装入物品：[0, 1, 2]
箱子1-装入物品：[3, 4, 5]
箱子2-装入物品：[6, 7]
箱子3-装入物品：[8, 9, 10]