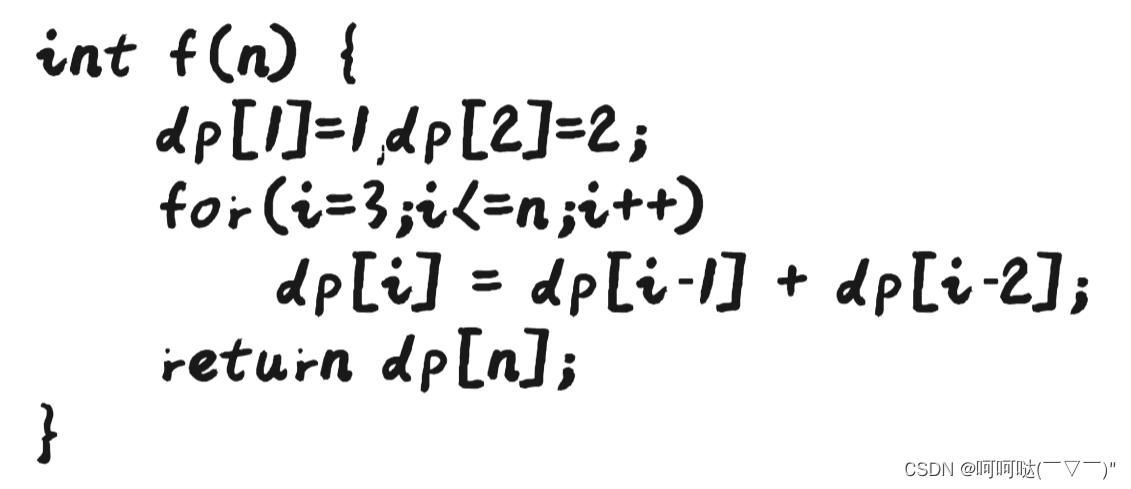代码随想录算法训练营第四十一天 | LeetCode 416. 分割等和子集
文章链接:01背包理论基础 01背包理论基础(滚动数组) 分割等和子集
视频链接:01背包理论基础 01背包理论基础(滚动数组) 分割等和子集
1. 01 背包理论基础
1.1 思路
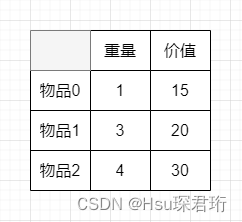
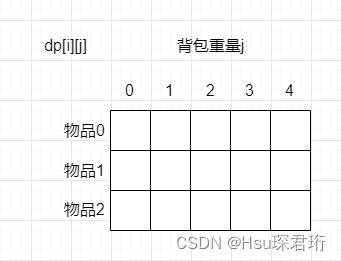
- 二维 dp 数组及其下标的含义:dp[i][j]:[0,i] 的物品中任取,放入容量为 j 的背包,价值总和最大是多少
- 确认递推公式:
a. 不放物品 i,背包容量为 j 的最大价值为 dp[i-1][j]
b. 放物品 i:背包容量为 j-weight[i] 的最大价值为 dp[i-1][j-weight[i]]+value[i]。翻译一下即背包容量减去物品 i 的容量 dp[i-1][j-weight[i]] 所能放的最大价值+物品 i 的价值。可以这么理解:放了物品 i,还剩下 j - weight[i] 的容量可以放其他物品,剩下空间能得到的最大价值是 dp[i-1][j-weight[i]]
c. 上面两个当然是取最大值了,因为我们要求价值最大,因此递推公式:dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]) - dp 数组的初始化:根据递推公式 dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])可以看出不放物品 i 的话是由该位置的正上方推导出来的,放物品 i 的话是由该位置的左上方推导出来的,因此第一行和第一列都要初始化,这样别的位置就都能由它们推导出来了。
- 首先是第一列,背包容量都为 0 了,那自然物品都放入不了,价值为 0,因此第一列全初始化为 0
- 然后是第一行,只放物品 0,背包容量 j,如果 j >= weight[0](即物品 0),那么 dp[0][j] 就初始化为 value[0];如果 j<weight[0] 那么 dp[0][j] 就初始化为 0
- 至于其他位置的初始化,其实初始化为什么都可以,因为我们的递推公式是能把这个其他 dp[i][j] 位置的值给覆盖的
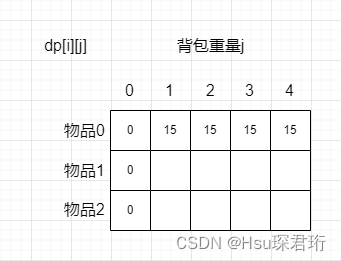
- 遍历顺序:二维 dp 数组的遍历很讲究。要两层 for循环,一层 for循环遍历物品,一层 for循环遍历背包容量。那么第一层物品第二层背包还是第一层背包第二层物品呢?答案是都可以
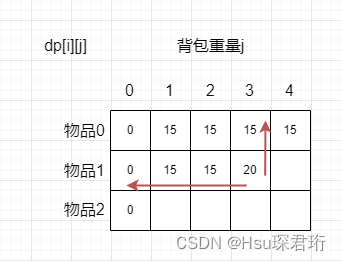
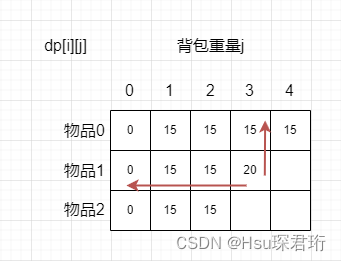
- 当前 dp[i][j] 的值是由正上方和左上方推导出来的。因为由于 dp[i-1][j] 和 dp[i - 1][j - weight[i]] 都在正上方和左上方,所以即使遍历次序不同,dp[i][j] 所需要的数据就是在正上方或左上角,不影响推导,不管是哪种遍历方式,dp[i][j] 的正上方或左上角总会有值,总能把 dp[i][j] 填上去
- 打印 dp 数组:主要用于 debug
1.2 代码
public class BagProblem {
public static void main(String[] args) {
int[] weight = {1,3,4};
int[] value = {15,20,30};
int bagSize = 4;
testWeightBagProblem(weight,value,bagSize);
}
/**
* 动态规划获得结果
* @param weight 物品的重量
* @param value 物品的价值
* @param bagSize 背包的容量
*/
public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){
// 创建dp数组
int goods = weight.length; // 获取物品的数量
int[][] dp = new int[goods][bagSize + 1];
// 初始化dp数组
// 创建数组后,其中默认的值就是0
for (int j = weight[0]; j <= bagSize; j++) {
dp[0][j] = value[0];
}
// 填充dp数组
for (int i = 1; i < weight.length; i++) {
for (int j = 1; j <= bagSize; j++) {
if (j < weight[i]) {
/**
* 当前背包的容量都没有当前物品i大的时候,是不放物品i的
* 那么前i-1个物品能放下的最大价值就是当前情况的最大价值
*/
dp[i][j] = dp[i-1][j];
} else {
/**
* 当前背包的容量可以放下物品i
* 那么此时分两种情况:
* 1、不放物品i
* 2、放物品i
* 比较这两种情况下,哪种背包中物品的最大价值最大
*/
dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);
}
}
}
// 打印dp数组
for (int i = 0; i < goods; i++) {
for (int j = 0; j <= bagSize; j++) {
System.out.print(dp[i][j] + "\t");
}
System.out.println("\n");
}
}
}
2. 01 背包动态规划理论基础(滚动数组)
2.1 思路
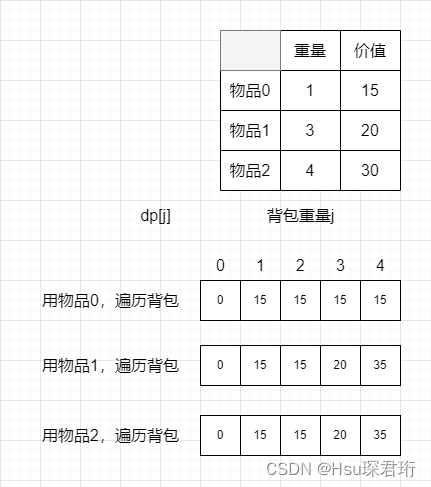
- 在使用二维数组时递推公式:dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])即当前层的数值是由正上方和左上方(即上一层)推导出来的。而我们可以把数据拷贝到第 i 层,直接在第 i 层计算,这就是滚动数组的由来,也就是为什么可以把二维降为一维
- 确定 dp 数组及其下标的含义:我们用 dp[j] 表示方便和二维数组dp[i][j] 的 j 保持同一个意思,方便理解。dp[j] 表示容量为 j 的背包,所背的物品的最大价值为 dp[j]
- 递推公式:在二维数组的递推公式中我们是由放物品 i 和不放物品 i 的状态中取最大值,一维数组也是一样的,dp[j]=Math.max(dp[j],dp[j-weight[i]+value[i]),不放物品 i 就是 dp[j],表示覆盖原来的数据,放物品 i 就是去掉物品 i 容量的最大价值+物品 i 的价值就是当前 j 容量的最大价值
- dp 数组的初始化:dp[0] 表示背包容量为 0 的最大价值,那当然是 0 了,因为没有物品的重量为 0 可以放入背包中;非 0 下标,看递推公式 dp[j]=Math.max(dp[j],dp[j-weight[i]+value[i]),可以看出当前值是由前一个值加上 value[i] 和本身 dp[j] 比较取最大值,那既然和本身取最大值,初始化时就应该把它初始化为非负数里的最小值即可(也就是 0),那初始化时就不会初始化一个数值会把比较中本来应该计算的数值给覆盖掉了。这里虽然是直接全部初始化为 0,但也是经过思考的,而不是尝试着全为 0 或者全为 1 这样子
- 遍历顺序:大多数人知道的都是直接两层 for循环 for(int i=0;i<物品数量;i++)for(int j=bagweight;j>=weight[i];j–)即先物品再背包,背包那一层是倒序。首先看为什么倒序呢?是为了保证每个物品只被添加过一次。那为什么先物品再背包呢?反过来行不行?因为我们背包容量是倒序遍历的,如果先遍历背包容量,那么每个 dp[j] 只会放入一个物品,即:背包中只放入了一个物品

- 打印 dp 数组:主要用于 debug
2.2 代码
public static void main(String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWight = 4;
testWeightBagProblem(weight, value, bagWight);
}
public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){
int wLen = weight.length;
//定义dp数组:dp[j]表示背包容量为j时,能获得的最大价值
int[] dp = new int[bagWeight + 1];
//遍历顺序:先遍历物品,再遍历背包容量
for (int i = 0; i < wLen; i++){
for (int j = bagWeight; j >= weight[i]; j--){
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
//打印dp数组
for (int j = 0; j <= bagWeight; j++){
System.out.print(dp[j] + " ");
}
}
3. LeetCode 416. 分割等和子集
3.1 思路
- 如果能找到集合中出现总和为 sum/2 子集总和,就认为 true。而且这种背包问题要注意元素是否可以重复,本题是不可以重复的,每个元素只能使用一次,然后集合里的元素能不能装满 sum/2 这么个背包。
- dp 数组及其下标的含义:dp[j] 容量为 j 的背包的最大价值为 dp[j]。可能会疑惑,本题也没有什么物品的重量和价值啊?本题的数值既是它的重量也是它的价值。那我们把背包容量为 sum/2 装满后的价值也是 sum/2。target=sum/2。如果最后 dp[target]==target 那就是 true 了
- 递推公式:dp[j]=Math.max(dp[j],dp[j-nums[i]]+nums[i])。不了解的可以看上面 01 背包理论基础 和 01 背包动态规划理论基础(滚动数组)部分
- dp 数组的初始化:dp[0]=0,容量为 0 的背包最大价值自然也为 0。非 0 下标也是初始化为 0,因为后续求 dp[j] 时都是用前一个值加上 nums[j] 和本身作比较取最大值的然后把 dp[j] 覆盖的,如果初始化为很大,那就覆盖不了
- 遍历顺序:是先物品再背包,for(int i=0;i<nums.length;i++)for(int j=target;j>=nums[i];j–)如果 j 比 nums[i] 还小就放不进去背包了
- 打印 dp 数组:用于 debug
3.2 代码
class Solution {
public boolean canPartition(int[] nums) {
if(nums == null || nums.length == 0) return false;
int n = nums.length;
int sum = 0;
for(int num : nums) {
sum += num;
}
//总和为奇数,不能平分
if(sum % 2 != 0) return false;
int target = sum / 2;
int[] dp = new int[target + 1];
for(int i = 0; i < n; i++) {
for(int j = target; j >= nums[i]; j--) {
//物品 i 的重量是 nums[i],其价值也是 nums[i]
dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
}
//剪枝一下,每一次完成內層的for-loop,立即檢查是否dp[target] == target,優化時間複雜度(26ms -> 20ms)
if(dp[target] == target)
return true;
}
return dp[target] == target;
}
}