一、符号执行概念
符号执行(Symbolic Execution)是一种程序分析技术,它
可以通过分析程序来得到让特定代码区域执行的输入。
符号执行的
目的
是在给定的时间内,
生成一组输入,并通过这些输入尽可能多的探索执行路径。根据运行目的来分,主要有两个:
-
从测试的角度来看,它可以模拟出各个路径的输入值,从而创建高覆盖率的测试套件。
-
从缺陷查找的角度来看,它为开发人员提供了触发缺陷的具体输入,利用该输入,程序可用于缺陷的确认与调试。符号执行不仅限于查找诸如缓冲区溢出之类的问题,而且可以通过根据缺陷发现的条件,生成复杂的断言,来判断缺陷发生的可能性。
符号执行的优势是能够以尽可能少的测试用例达到高测试覆盖率,从而挖掘出复杂软件程序的深层错误。但会受到
路径爆炸问题、
约束求解困、
内存建模等问题。
符号执行经过了
传统符号执行→动态符号执行
→
选
择
性符
号
执行
的发展过程,动态符号执行包括
混合测试
和
执
行
生
成
测试两种。
-
经典符号执行并不真实地执行,而是基于解析程序,通过符号值模拟执行;有代价小、效率高的优点,但是执行效率比较低、误报高。
-
动态符号执行结合使用了具体执行与符号执行,综合了具体执行和经典符号执行的优点,并出现了 混合执行 和 执行生成测试 两种符号执行技术;
-
选择性符号执行可以对程序员感兴趣的部分进行符号执行,其它部分用真实值执行,代表工具 S2E 。
二、经典符号执行
经典符号执行的核心思想是通过使用符号值来代替具体值作为程序输入,并用符号表达式来表示与符号值相关的程序变量的值。在遇到程序分支指令时,程序的执行也相应地搜索每个分支,分支条件被加入到符号执行保存的程序状态的PC中,PC表示当前路径的约束条件。在收集了路径约束条件之后,使用约束求解器来验证约束的可解性,以确定该路径是否可达。若该路径约束可解,则说明该路径是可达的;反之则说明该路径不可达,结束对该路径的分析。
这里举一个经典的例子,来说明符号执行的具体过程
:
1 int twice(int v){
2 return 2*v;
3 }
4
5 void testme(int x, int y){
6 z = twice(y);
7 if (z == x){
8 if (x > y+10)
9 ERROR;
10 }
11 }
12
13 int main(){
14 x = sym_input();
15 y = sym_input();
16 testme(x, y);
17 return 0;
18 }
这段代码中的testme()有三条执行路径。
符号执行的目的,就是在给定的时间预算内,生成一组输入,并通过这些输入尽可能多的探索执行路径。
-
执行路径(execution path):一个true和false的序列seq={p0,p1...,pn}。其中,如果是一个条件语句,那么pi=true则表示条件语句的取值为:true,否则取false;
-
执行树(execution tree):一个程序的所有执行路径则可表征成一颗执行树。
下图是样例代码的执行树:
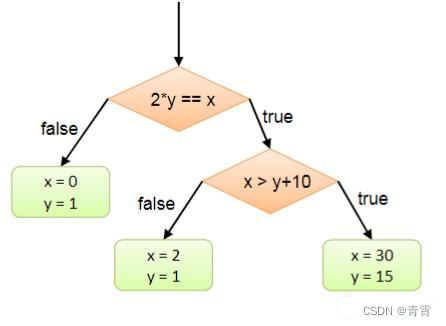
符号执行通过维护
符号状态
和
路径约束
,以便在运行过程中传递信息。
-
符号状态(symbolic state):符号执行维护一个 符号状态 σ,将变量映射到符号表达式;
-
符号路径约束(symbolic path constraint): 符号路径约束PC,它是符号表达式上无量词的一阶公式;
-
在执行开始时,将符号状态σ初始化为一个空映射,将符号路径约束PC初始化为true;
-
在符号执行过程中,符号状态σ 和 符号路径约束PC都会更新;
-
在沿着程序执行路径的符号执行结束时, 使用约束求解器对符号路径约束PC进行求解,以生成具体的输入值。如果程序在这些具体的输入值上执行,它将采用与符号执行完全相同的路径并以相同的方式终止。
对于样例代码,具体过程如下
:

经典的符号执行有一个关键的
缺点
,若符合执行路径的符号路径约束无法使用约束求解器进行有效的求解,则无法生成输入。
三、现代符号执行技术
经典的符号执行,过度依赖符号执行的约束求解能力,这就限制了传统符号执行的能力发挥。
如果能加入具体值进行分析,将大大简化分析过程,降低分析的难度和提升效率;但分析过程中,仍不可避免的还是需要将各种条件表达式,进行符号化抽象后变成约束条件参与执行。将程序语句转换为符号约束的精度,对符号执行所达到的覆盖率以及约束求解的可伸缩性会产生重大影响。
所以如何做好混合具体(Concrete)执行和符号(Symbolic)执行的能力的平衡,就成为现代符号执行的关键点。

混合执行测试(Concolic testing)和执行生成测试(Execution-Generated Testing (EGT))这两种现代符号执行的代表都是基于这个思想发展而来的。
3.1、混合执行测试
下面以混合执行测试(Concolic testing)为例说明下现代符号执行的主要过程。

与经典的符号执行不同,由于混合执行在整个执行过程中,需要维护程序的具体状态,因此其输入需要初始具体值。
混合执行测试从一个给定的输入或随机输入开始执行程序,沿着执行的条件语句在输入上收集符号约束,然后使用约束求解推断先前输入的变化,以便引导程序接下来的执行该走向哪一个执行路径。重复此过程,直到探索了所有执行路径,或者满足用户定义的覆盖标准、时间设置到期为止。
混合执行测试会同时维护两个状态:
-
具体状态:映射所有有具体值的变量;
-
符号状态:仅映射没有具体值的变量。
对于样例代码,执行过程如下:
比较混合执行测试和传统的符号执行,不难发现由于具体值的引入,简化了约束求解的难度。
3.2、执行生成测试
执行生成测试也融合了具体执行与符号执行的软件测试技术,由斯坦福大学 Cristian等提出并在 EXE中实现。
执行生成测试与混合测试最大的不同点在于将符号执行与具体执行混合的方式不同。执行生成测试的混合是在一次程序执行中,对符号变量无关的代码段使用具体执行,而对符号变量有关的代码段进行符号执行,使用符号执行引导测试过程,为每条路径生成一个测试用例,并进行一次执行。
与混合测试相比,执行生成测试的优势是能更加系统且高效地得到所有的路径信息以及对应的测试用例,避免重复性搜索过程;其缺点是内存空间耗费较大,一种解决思路是可以使用多线程的方式代替分支存储,实现对多个分支的同时搜索和测试用例的生成。
执行生成测试的核心思想是通过程序代码自动地生成潜在的高度复杂的测试用例,在用符号输入执行程序的过程中,在分支处将false路径的状态信息记录下来,判断为true的分支继续执行。记录其约束信息,通过求解这些约束信息得到该路径的测试用例,该分析过程就是执行生成测试。
对于样例代码,执行过程如下:
3.3、选择性符号执行
受路径爆炸与约束求解问题的制约,符号执行不适用于程序规模较大或逻辑复杂的情况。选择性符号执行可以解决这类问题。
选择性符号执行也是具体执行与符号执行混合的一种分析技术,依据特定的分析,决定符号执行与具体执行的切换使用。在选择性符号执行中,用户可以制定一个完整系统中的任意感兴趣额的部分进行符号执行分析,可以是应用程序、库文件、系统内核和设备驱动程序。选择性符号执行在符号执行和具体执行间无缝地来回转换,并透明地转换符号状态和具体状态。选择性符号执行极大地提高了符号执行在实际应用中对大型软件分析测试的可用性,且不再需要对这些环境进行模拟建模。

选择性符号执行的核心是符号执行和具体执行的交互处理,即在具体执行转入符号执行区域及符号执行转入具体执行时的处理。
四、挑战与解决方案
符号执行仍存在路径爆炸(代码规模、复杂度)、约束求解(计算算法)、内存模型(工具设计)等挑战。
4.1、路径爆炸(Path Explosion)
因为在符号执行的分析过程中,在每个分支节点,符号执行都会衍生出两个符号执行实例,程序分支路径的数量与程序分支的数量呈指数级增长关系。
以下图的代码为例,代码中共有3个分支判断语句和1个循环语句,3个分支判断语句,根据x,y,z值的不同,将会产生8条不同的程序路径;而对于循环来说,当a取最大值时,该循环将会产生231条路径。

符号执行在过程处理中默认已经过滤了以下两种路径:
-
不依赖于符号输入的路径
-
对于当前的路径约束,不可解的路径。
但是,尽管符号执行已经做了这些过滤,路径爆炸依旧是符号执行的最大挑战。路径爆炸不是符号执行特有的挑战,是整个程序分析都需要考虑的最大的问题。
解决路径爆炸的方案,可以从以下两个角度来考虑:
-
减少路径总数(优先的考虑最有希望的路径, 路径合并,剪枝);
-
相似的路径不再分析(函数摘要,缓存);
依据这个思路业界提出了两种解决方案:
-
启发式(Heuristic): 大多数启发式方法侧重于实现较高的语句和分支覆盖率。
a)特别有效的方法是使用静态控制流图(CFG)来指导探索,向最接近的路径或优先选择先前执行次数最少的语句;
b)在每个可行的符号分支,随机选择要探索的一侧; 或者将符号检验与随机检验进行交错进行;
c)采用先验知识,探索以往容易出错的函数;目前也有研究通过AI的方式得到这些推荐的分析路径;
-
利用完善的程序分析技术(Sound program analysis techniques): 这种方法主要是使用程序分析和软件验证中的各种思想,以合理的方式降低路径探索的复杂性。
a)静态地合并路径,然后再求解;
b)通过函数摘要,缓存或重用已经计算过的信息用于后续的计算中;
c)通过剪枝,去除无关的变量对路径的求解的影响;
4.2、约束求解(Constraint Solving)
-
减少不相关的约束(Irrelevant constraint elimination) 符号执行中的绝大多数查询是为了确定某个分支的可行性,一种有效的优化方法是从路径条件中删除与当前分支的结果无关的那些约束。
-
增量求解(incremental solving) 符号执行期间生成的约束集的一个重要特征是,它们根据来自程序源代码的一组固定的静态分支来表示。因此,许多路径具有相似的约束集,因此可以采用相似的解决方案。
a)通过重用先前类似查询的结果,来提高约束求解的速度;
b)通过约束集的超集,减少无解的情况出现; 我们目前常用的符号执行的工具KLEE,在设计中都采用了着两种方式。

4.3、内存建模(Memory Modeling)
在符号执行中我们将变量映射到了一个内存模型,来表示这个变量的类型、值或者值域。这个对变量的抽象模式对程序语句转化成符号约束的精度和对符号执行的覆盖率有着很大的影响。太过精确,往往容易陷入复杂的计算,而不能得到具体的解;太过笼统,又会造成漏报。所以精度和可扩展性之间是需要权衡的。
目前这个权衡的主要参考依据是:
-
具体分析问题的性质;
-
采用的约束求解器的限制;
四、符号执行工具
|
语言
|
符号执行器
|
链接
|
备注信息
|
|
LLVM
|
KLEE
|
https://klee.github.io/
|
Cadar et al., 2006
|
|
LLVM
|
Cloud9
|
http://cloud9.epfl.ch/
|
Bucur et al., 2011,基于KLEE的并行符号执行
|
|
LLVM
|
Kite
|
http://www.cs.ubc.ca/labs/isd/Projects/Kite/
|
do Val, 2014, 基于KLEE
|
|
Java
|
JPF-Symbc
|
https://github.com/SymbolicPathFinder/jpf-symbc
|
2008, 用于测试NASA的软件
|
|
Java
|
jayhorn
|
http://jayhorn.github.io/jayhorn/
|
基于soot,支持Z3, 2016
|
|
Java
|
JDart
|
https://github.com/psycopaths/jdart
|
Luckow et al., 2016
|
|
Python
|
PyExZ3
|
https://github.com/thomasjball/PyExZ3
|
Ball and Daniel,2015
|
|
JavaScript
|
Jalangi
|
https://github.com/Samsung/jalangi2
|
Sen et al., 2013
|
|
Binaries
|
angr
|
http://angr.io/
|
Shoshitaishvili et al., 2015, python框架
|
目前符号执行,在实际的应用中还主要用于与fuzz结合使用,用于缩小fuzz的取值范围。由于符号执行的主要瓶颈--约束求解的性能和局限性,并未在静态分析的商业工具中,大规模的使用。但我们有理由相信,在不久的将来随着并行技术、计算性能的提升、以及求解器的优化,符号执行能够在静态分析中发挥越来越大的作用