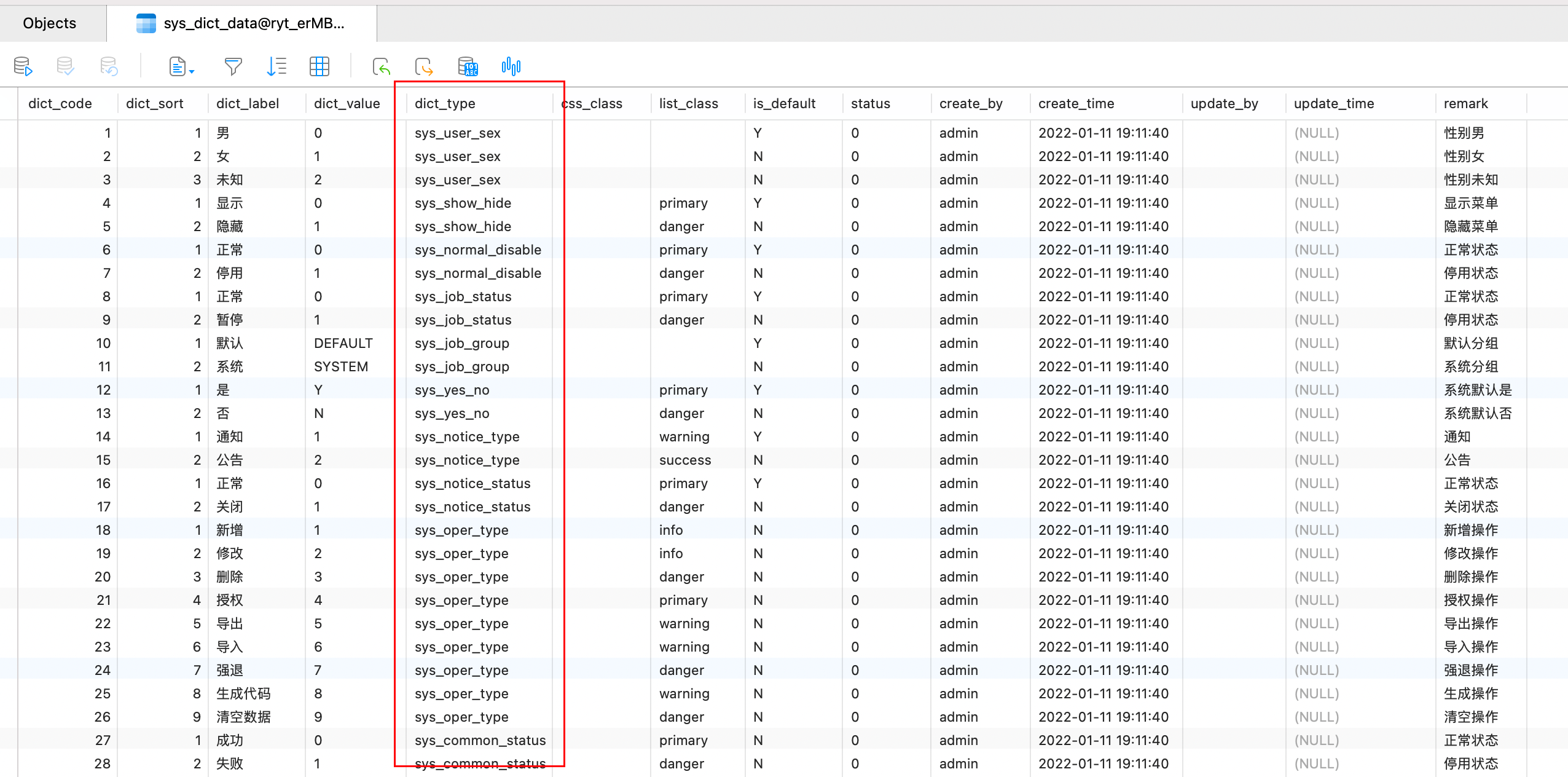
什么是布隆过滤器

布隆过滤器其实本质上来讲就是一种巧妙的数据结构，特点就是高效的插入和查询。

它能告诉我们：什么一定不存在，或者什么可能会存在

总结：布隆过滤器是概率性的。它只能告诉我们什么一定不存在，或者什么有可能存在

布隆过滤器能解决什么问题

一、解决缓存穿透的场景：

倘若查询大量不存在的数据，查询缓存 -> 查询DB，此时都缓存一直没数据，就会一直查DB，则为缓存穿透

使用布隆过滤器，能够拦截大量查询不存在数据的请求，以免大量的查询走到DB那一层

二、大集合查询某一个具体的数据的场景（比如一亿个用户系统中查询某个用户是否下过单）

总结：以上两种场景都有一个共性，判断一个元素是否在某一个集合中。使用布隆过滤器能够有效解决此场景的问题。

布隆过滤器的原理

一、哈希函数

哈希函数：将任意大小的数据经过转换，得到了特定大小的数据。譬如，原数据为userPhone，经hash函数转换后得到的数据即为hash code。

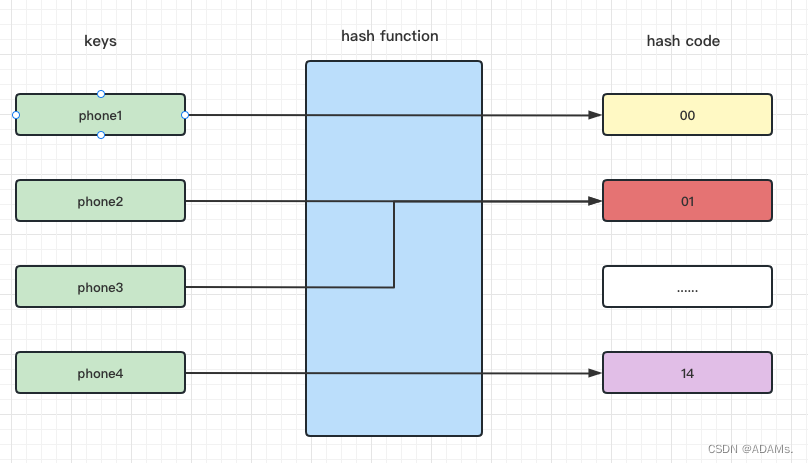
如图所示，phone1经过hash函数转换后得到了hash code = 00，而phone2、phone3经过hash函数转换后得到了hash code = 01。

由此可知，数据得到了压缩，且哈希函数是实现布隆过滤器的基础。

二、数据结构

布隆过滤器的数据结构其实就是一个bit数组，具体的结构如下所示：

如图所示，其结构每一个下标所对应的数值都对应的是0、1制的数据值。

三、执行原理

假设有2个元素 {x ， y}，且当前布隆过滤器设置了2个hash函数。此时x，y两个元素经过hash函数映射得到的数据结果如下图所示

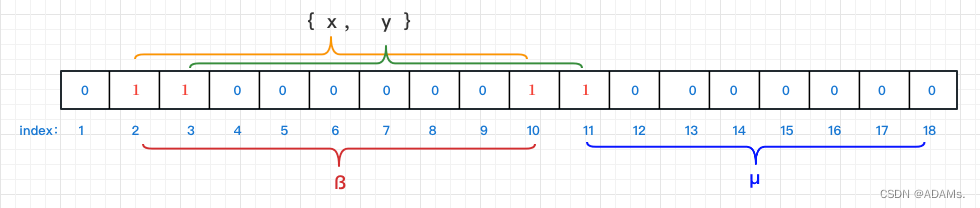
• 由图可知， {x ， y}经过2个hash函数的映射，分别占用index = [ 2 , 10 ]、[ 3 , 11 ]；此时我们的这些index下标，所对应的value值由0改为了1。
• 查询 µ 是否在集合里，首先将 µ 分别经过2个hash函数映射，得到index = [ 11 , 18 ]的value值：index[11] = 1，index[18] = 0；由于index[18] = 0（存在一个下标所对应的value为0的数值，此元素必然不存在集合中，因此 µ 必然不在集合中）
• 查询 ß 是否在集合中，其经过2个hash映射分别得到index = [ 2 , 10 ]的value值：index[2] = 1，index[10] = 1；（由于其所映射的index下标所对应的value都为1，因此 ß 有可能存在集合中 ）

PS：此处的数据存在集合中，是非必然存在的，而是有可能存在，存在一定的误判几率；

假设 ß 经过hash函数映射得到index = [ 2 , 10 ]，虽然这2个下标所对应的value都是1，但是 [ 2 , 10 ] 有可能是由不同元素经过hash函数映射出来的下标值。

因此这种情况说明 ß 经过hash函数映射得到index = [ 2 , 10 ]，其也并非绝对是一个元素经过hash函数映射过来的，故此存在误判的可能。

总结：布隆过滤器经过hash函数映射得到值都是1，则说明数据可能会存在；但是某一位数值是0，则说明数据一定不存在

布隆过滤器的业务实现方式

代码实现可以参考redisson的bloom filter，或者使用goove包的布隆过滤器（不详细展开，可参考网上代码）

业务接入流程：

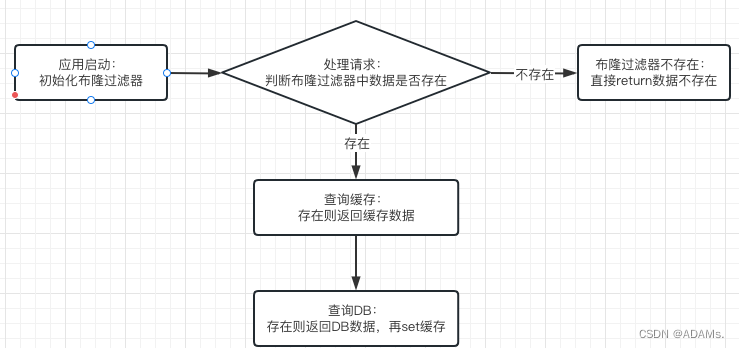
布隆过滤器的美与不美

美之所在：

1. 能够过滤大部分的无效请求，譬如查询一个不存在的数据，直接可通过布隆过滤器拦截无效请求。
2. 针对高并发场景，在保护系统层面起到一定程度的作用
3. 概念简单，性能较好

不美之所在：

1. 存在误判率（误判率可以通过：增加数组长度、增加hash次数等方式来进行，但是代价是其会让布隆过滤器的性能降低，CPU需要运算更多的内容）
2. 无法删除布隆过滤器中的数组数据（倘若布隆过滤器需要重新刷新数据，建议使用定时器定时创建一个新的布隆过滤器，废弃旧的布隆过滤器）
3. hash函数个数和布隆过滤器的数组长度不好定义
   1. 倘若布隆过滤器数组长度过小，那么数组的所有bit位都会变成1，就起不到过滤的作用了
   2. hash函数的个数也不宜过多，倘若hash函数太多，则数组所有bit位都变为1的速度也会过快
   3. 倘若hash函数太少，误报率也会变高，譬如所有数据都只经过1次hash，那么hash碰撞的概率极大，所得到的bit位重复概率也会随之增多
4. 首次初始化布隆过滤器存在一定的代价，倘若数据量过大，初始化工作量和复杂度也会增加