目录
一、模拟算法题目
(1)神奇的幻方
(2)Proceting the Flower
(3)排座椅
(4)国王的游戏
(5)字典序最大的子序列
一、模拟算法题目
(1)神奇的幻方
题目链接:神奇的幻方
题解:对于本题,其实难度不是很大,就是模拟,因为这是典型的模拟,锻炼了思维,所以我对于本题做了笔记。读了题我们知道从1到n*n我们对于每个数一个一个开始模拟,根据上一个数的状态推出当前数的状态。所以我设了三个数组,heng[i]表示数i在第几行,lie[i]表示数i在第几列,a[i][j]表示i行列的数是多少,然后开始一个一个推。
#include<bits/stdc++.h> using namespace std; int n; int hang[1600],lie[1600]; int a[40][40]; int main() { cin>>n; hang[1]=1; lie[1]=(n+1)/2; a[1][lie[1]]=1; for(int i=2;i<=n*n;i++){ if(hang[i-1]==1&&lie[i-1]!=n){ hang[i]=n; lie[i]=lie[i-1]+1; a[hang[i]][lie[i]]=i; } else if(hang[i-1]!=1&&lie[i-1]==n){ hang[i]=hang[i-1]-1; lie[i]=1; a[hang[i]][lie[i]]=i; } else if(hang[i-1]==1&&lie[i-1]==n){ hang[i]=2; lie[i]=n; a[hang[i]][lie[i]]=i; } else{ int x=hang[i-1],y=lie[i-1]; if(a[x-1][y+1]==0){ hang[i]=x-1; lie[i]=y+1; a[hang[i]][lie[i]]=i; } else{ hang[i]=x+1; lie[i]=y; a[hang[i]][lie[i]]=i; } } } for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ if(j==n){ cout<<a[i][j]; } else{ cout<<a[i][j]<<" "; } } cout<<endl; } return 0; }
(2)Proceting the Flower
题目链接:Proceting the Flower
对于本题翻译成中文的意思是 :
农夫有n头牛跑到花田上吃草,农夫要把他们送回到自己的牛舍,所花的时间分别是t[i],单程时间是t[i],回来还要t[i],每头牛留在花田上每单位时间内吃花量为d[i]。求花田上最少被破坏的数量为多少?
题解:对于本题,假如a,b两头相邻的牛的顺序发送变化,假设a在b前,那么对于总体破坏花的数量 a前面并未发生变化,b后面也未发生变化,a前面并未与a,b相关,b后面是与总体相关,并未与个体相关。
推算如下:
#include<bits/stdc++.h> using namespace std; typedef long long ll; int n; typedef struct{ int t,d; }node; node a[100010]; struct rule{ bool operator()(node x,node y){ return x.t*y.d<y.t*x.d; } }; int main() { cin>>n; for(int i=0;i<n;i++){ cin>>a[i].t>>a[i].d; } sort(a,a+n,rule()); ll sum=0,t=0; for(int i=0;i<n;i++){ sum+=t*a[i].d; t+=2*a[i].t; } cout<<sum; return 0; }
(3)排座椅
题目链接:排座椅
题解:对于本题,横向和纵向是分开的,根据题意是想要分开更多的人交头接耳。那么根据题意横向分隔是不会影响行,纵向切割不影响列,所以如果分开哪一列或者哪一行的人数更多,就先用它,也就是需要排序。后面输出是根据序号从小到大,这也要注意。
#include<bits/stdc++.h> using namespace std; typedef long long ll; int n,m,k,l,d; typedef struct{ int num;//隔开的人数 int pos;//位置 }node; node hang[1100],lie[1100]; //该排序规则使得某一种分隔方法人数多的在前面 struct rule1{ bool operator()(node x,node y){ return x.num>y.num; } }; //该排序使得序号小的在前面 struct rule2{ bool operator()(node x,node y){ return x.pos<y.pos; } }; int main() { cin>>m>>n>>k>>l>>d; //序号位置初始化 for(int i=1;i<=m;i++){ hang[i].pos=i; } for(int i=1;i<=n;i++){ lie[i].pos=i; } for(int i=1;i<=d;i++){ int x,y,p,q; cin>>x>>y>>p>>q; if(x==p){ //在同一行,用竖线隔开 lie[min(y,q)].num++; } else{ //同一列,因为是交头接耳,所以只有这两种情况 hang[min(x,p)].num++; } } sort(hang+1,hang+1+m,rule1()); sort(lie+1,lie+1+n,rule1()); sort(hang+1,hang+1+k,rule2()); sort(lie+1,lie+1+l,rule2()); for(int i=1;i<=k;i++){ if(i==k){ cout<<hang[i].pos; } else{ cout<<hang[i].pos<<" "; } } cout<<endl; for(int i=1;i<=l;i++){ if(i==l){ cout<<lie[i].pos; } else{ cout<<lie[i].pos<<" "; } } return 0; }
(4)国王的游戏
题目链接:国王的游戏
题解:本题应该用高精度算法,但是我只想写下这种类型的题目具体思路,方便以后复习,所以就没有写全,不能完全AC(加上高精度即可AC)。
本题与第二题一样的思路,都是推理,两个位置的相对交换对于前后没有影响,只对于他们两有变化,具体推理如下:
#include<bits/stdc++.h> using namespace std; typedef long long ll; int n; typedef struct{ int l,r; }node; struct rule{ bool operator()(node x,node y){ return x.l*x.r<y.l*y.r; } }; node a[1100]; int main() { cin>>n; for(int i=0;i<=n;i++){ cin>>a[i].l>>a[i].r; } sort(a+1,a+1+n,rule()); // cout<<"sort后"<<endl; ll sum=a[0].l; sum=sum*a[1].l; for(int i=2;i<n;i++){ //注意是i<=n,不能等于n,因为是前一个大臣左手的数,不包括自己的左手 sum=sum*a[i].l; } // cout<<"sum="<<sum<<endl; cout<<sum/a[n].r; return 0; }
(5)字典序最大的子序列
题目链接:字典序最大的子序列
题解:对于本题,字典序最大得子序列,先创建一个字符,每一添加点前字符串的字符,遍历每个字符,从后往前,字符小就删除。
#include<bits/stdc++.h> using namespace std; string s,ans; int main() { cin>>s; int l=s.size(); for(int i=0;i<l;i++){ while(ans.size()&&ans.back()<s[i]){ ans.pop_back(); } ans+=s[i]; } cout<<ans; return 0; }
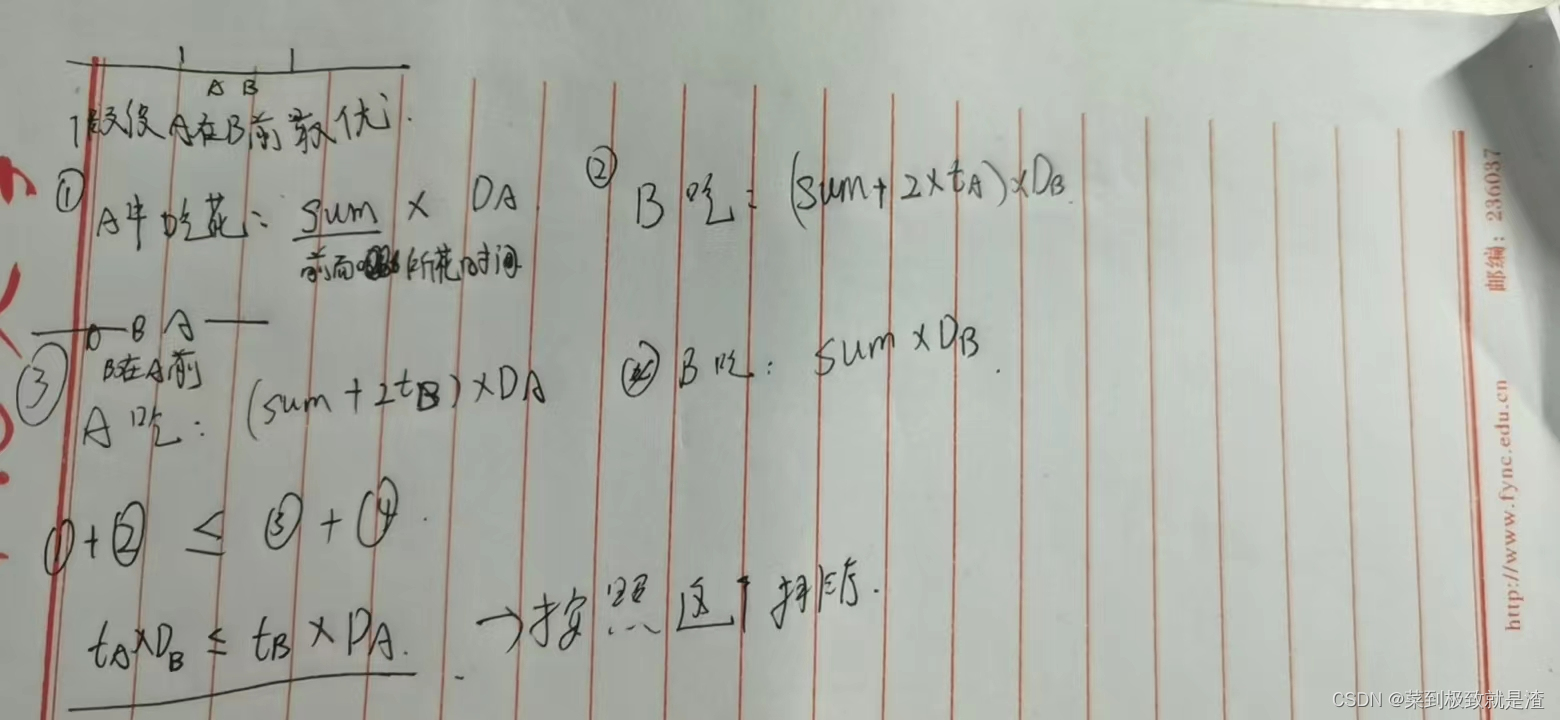







![[oeasy]python0033_任务管理_jobs_切换任务_进程树结构_fg](https://img-blog.csdnimg.cn/img_convert/e80bff55718950abc63889b3d44520da.png)



![[HAL库]STM32 ADC功能和DMA读数据的方法](https://img-blog.csdnimg.cn/54b7e8d96f214b03a39393a56cc881b3.png)