一、题目解析
题目链接：有效三角形的个数
我们知道想要组成一个三角形那么其任意两边之和必定大于第三边，即
但是如果我们知道这三条边的大小顺序，那么只需判断一次即可，假设c是最大的那条边，那么不等式②和③不用判断自然也就成立了。
二、算法原理
解法一：排序+暴力求解(时间复杂度：O(n^3)）
三层for循环枚举出所有的三元组，并且判断是否能构成三角形，但是这个暴力求解也是可以稍微优化一下的，对原数组进行排序，在判断较小的两条边之和大于第三边即可，不过也会超时。
class Solution {
public:
int triangleNumber(vector<int>& nums) {
sort(nums.begin(), nums.end());
int ret = 0;
int n = nums.size();
for(int i = 0; i < n; i++)
{
for(int j = i + 1; j < n; j++)
{
for(int k = j + 1; k < n; k++)
{
if(nums[i] + nums[j] > nums[k])
{
ret++;
}
}
}
}
return ret;
}
};解法二：排序+双指针（时间复杂度：O(n^2)）
- 排序
- 先固定最大的数
- 在最大的数的左区间内，使用双指针算法，快速统计出符合要求的三元组的个数
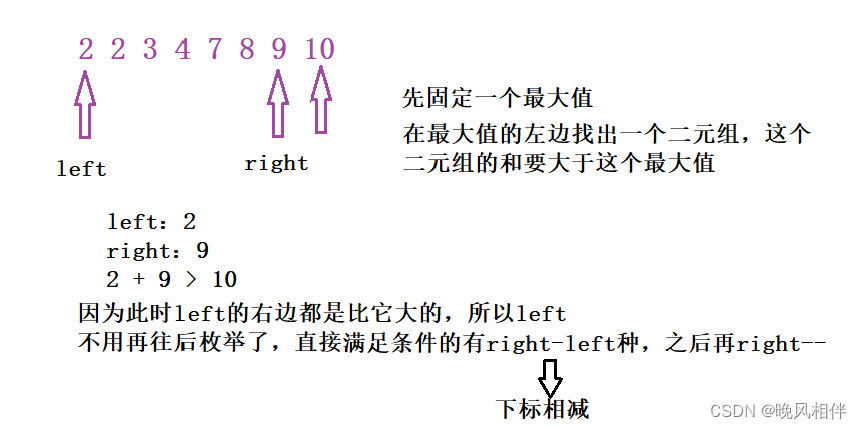
这种方法可以减少枚举的次数，最后再固定下一个最大值继续重复此方法向后枚举。
三、代码编写
class Solution {
public:
int triangleNumber(vector<int>& nums) {
sort(nums.begin(), nums.end());
int ret = 0;
int n = nums.size() - 1;
for(int i = n; i >= 2; i--)
{
int left = 0, right = i - 1;
while(left < right)
{
if(nums[left] + nums[right] > nums[i])
{
ret += right - left;
right--;
}
else
{
left++;
}
}
}
return ret;
}
};如有写的不好或有错误的地方还望指出，谢谢
