【数据结构复习之路】数组和广义表（严蔚敏版）万字详解主打基础

专栏：数据结构复习之路

复习完上面三章【线性表】【栈和队列】【串】，我们接着复习数组和广义表，这篇文章我写的非常详细且通俗易懂，看完保证会带给你不一样的收获。如果对你有帮助，看在我这么辛苦整理的份上，三连一下啦

一、数组的定义

二、数组的顺序表示和实现

三、矩阵的压缩存储

3.1、特殊矩阵

3.1.1、对称矩阵

3.1.2、三角矩阵

3.1.3、对角矩阵（带状矩阵）

3.2、稀疏矩阵(超详细)

3.3、十字链表（稀疏矩阵的链式存储结构）

四、广义表的定义

4.1、广义表的性质

4.2、广义表的存储结构

4.1.1、链表表示（法1）

4.1.2、链表表示（法2）

4.1.3、广义表的深度递归算法

结尾

Reference

一、数组的定义

数组和广义表可看成是一种特殊的线性表，其特殊在于: 表中的元素本身也是一种线性表，。内存连续。根据下标在O(1)时间读/写任何元素。

数组特点：结构固定，定义后维数和维界不再改变。

数组基本操作：除了结构的初始化和销毁之外，只有取元素和修改元素值的操作

二、数组的顺序表示和实现

一般都是采用顺序存储结构来表示数组，但数组可以是多维的，并且存储数据元素的内存单元地址是一维的，因此，在存储数组结构之前，需要解决将多维关系映射到一维关系的问题。

两种顺序存储方式：

以行序为主序 (低下标优先)
以列序为主序 (高下标优先)

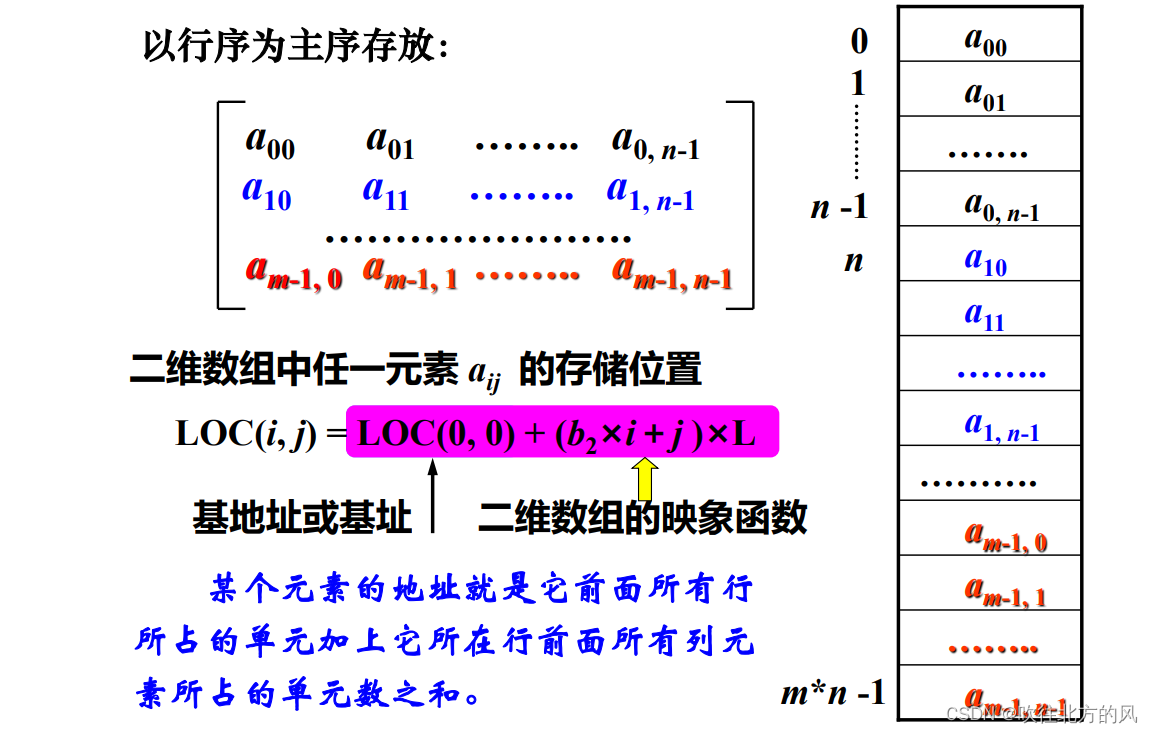
例题：

设数组 A[0…59, 0…69] 的基地址为 2048，每个元素占 2 个存储单元，若以列序为主序顺序存储，则元素 A[31, 57] 的存储地址为______。

同理，对三维数组A[b1 ][b2 ][b3 ],可以看成b1个b2 × b3的二维数组，若首元素的存储地址为LOC[0,0,0]，则按行序为主序存放。

则元素 $a_{i00}$ 的存储地址为 LOC( i , 0 , 0) = LOC(0,0,0) + ( i × b2 × b3 ) * L

这是因为该元素之前有 i 个b2× b3的二维数组.

所以 $a_{ijk}$ 的存储地址为 LOC( i , j , k) = LOC(0,0,0) + ( i × b2 × b3 + j × b3 + k) * L

推广到一般情况，可得到 n 维数组数据元素存储位置的映像关系：

LOC(j1 ,j2 ,…,jn )=LOC(0,0,0)+(b2×…×bn×j1+ b3×…×bn×j2+…+bn× jn-1+ jn ) × L

代码实现：（选择性掌握，可能有些学校不怎么考察）

5.1数组的定义&5.2数组的顺序表示和实现-CSDN博客

看完这个博客的介绍，你也许就能理解如下代码的实现了：

这里我构造一个a[3][4][2]的三维数组，并给出完整可运行代码，自己参悟（有详细注释）。

#include<stdarg.h>
#include<malloc.h>
#include<stdio.h>
#include<stdlib.h> // atoi()
#include<io.h> // eof()
#include<math.h>
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW 3
#define UNDERFLOW 4
typedef int Status; //Status是函数的类型,其值是函数结果状态代码，如OK等
typedef int Boolean; //Boolean是布尔类型,其值是TRUE或FALSE
typedef int ElemType;
#define MAX_ARRAY_DIM 8 //假设数组维数的最大值为8
typedef struct
{
    ElemType* base; //数组元素基址，由InitArray分配
    int dim; //数组维数
    int* bounds; //数组维界基址，由InitArray分配
    int* constants; // 数组映象函数常量基址，由InitArray分配，即每变化一维的跨度，方便计算出base数组对应的下标
} Array;
Status InitArray(Array& A, int dim, ...)
{
    //若维数dim和各维长度合法，则构造相应的数组A，并返回OK
    int elemtotal = 1, i; // elemtotal是元素总值
    va_list ap;
    if (dim<1 || dim>MAX_ARRAY_DIM)
        return ERROR;
    A.dim = dim;
    A.bounds = (int*)malloc(dim * sizeof(int));
    if (!A.bounds)
        exit(OVERFLOW);
    va_start(ap, dim);
    for (i = 0; i < dim; ++i)
    {
        A.bounds[i] = va_arg(ap, int); //依次取出bound1 = 3, bound2 = 4, bound3 = 2
        if (A.bounds[i] < 0)
            return UNDERFLOW;
        elemtotal *= A.bounds[i];
    }
    va_end(ap);
    A.base = (ElemType*)malloc(elemtotal * sizeof(ElemType));
    if (!A.base)
        exit(OVERFLOW);
    A.constants = (int*)malloc(dim * sizeof(int));
    if (!A.constants)
        exit(OVERFLOW);
    A.constants[dim - 1] = 1; //一维跨度为1
    for (i = dim - 2; i >= 0; --i)
        A.constants[i] = A.bounds[i + 1] * A.constants[i + 1]; //计算其余维度跨度
    return OK;
}
Status DestroyArray(Array* A)
{
    //销毁数组A
    if ((*A).base)
    {
        free((*A).base);
        (*A).base = NULL;
    }
    else
        return ERROR;
    if ((*A).bounds)
    {
        free((*A).bounds);
        (*A).bounds = NULL;
    }
    else
        return ERROR;
    if ((*A).constants)
    {
        free((*A).constants);
        (*A).constants = NULL;
    }
    else
        return ERROR;
    return OK;
}
Status Locate(Array A, va_list ap, int* off) // Value()、Assign()调用此函数 */
{
    //若ap指示的各下标值合法，则求出该元素在A中的相对地址off

    int i, ind;
    *off = 0;
    for (i = 0; i < A.dim; i++)
    {
        ind = va_arg(ap, int);
        if (ind < 0 || ind >= A.bounds[i])
            return OVERFLOW;
        *off += A.constants[i] * ind;
    }
    return OK;
}
Status Value(ElemType* e, Array A, ...) 
{
    //依次为各维的下标值，若各下标合法，则e被赋值为A的相应的元素值
    va_list ap;
    Status result;
    int off;
    va_start(ap, A);
    if ((result = Locate(A, ap, &off)) == OVERFLOW) //调用Locate()
        return result;
    *e = *(A.base + off);
    return OK;
}
Status Assign(Array* A, ElemType e, ...)
{
    //依次为各维的下标值，若各下标合法，则将e的值赋给A的指定的元素
    va_list ap;
    Status result;
    int off;
    va_start(ap, e);
    if ((result = Locate(*A, ap, &off)) == OVERFLOW) //调用Locate()
        return result;
    *((*A).base + off) = e;
    return OK;
}
int main()
{
    Array A;
    int i, j, k, * p, dim = 3, bound1 = 3, bound2 = 4, bound3 = 2; //a[3][4][2]数组
    ElemType e, * p1;
    InitArray(A, dim, bound1, bound2, bound3); //构造3＊4＊2的3维数组A
    p = A.bounds;
    printf("A.bounds=");
    for (i = 0; i < dim; i++) //顺序输出A.bounds
        printf("%d ", *(p + i));
    p = A.constants;
    printf("\nA.constants=");
    for (i = 0; i < dim; i++) //顺序输出A.constants
        printf("%d ", *(p + i));
    printf("\n%d页%d行%d列矩阵元素如下:\n", bound1, bound2, bound3);
    printf("将 i*100+j*10+k赋值给A[i][j][k]:\n\n") ; //运行结果1 
//    printf("将(i * 4 * 2 + j * 2 + k) * 4赋值给A[i][j][k]:\n\n") ; //运行结果2 
    for (i = 0; i < bound1; i++)
    {
        for (j = 0; j < bound2; j++)
        {
            for (k = 0; k < bound3; k++)
            {
            	Assign(&A, i * 100 + j * 10 + k, i, j, k); // 将i*100+j*10+k赋值给A[i][j][k]   
//            	Assign(&A, (i * 4 * 2 + j * 2 + k) * 4, i, j, k); // 将(i * 4 * 2 + j * 2 + k) * 4赋值给A[i][j][k]
                Value(&e, A, i, j, k); //将A[i][j][k]的值赋给e
                printf("A[%d][%d][%d]=%2d ", i, j, k, e); //输出A[i][j][k]
            }
            printf("\n");
        }
        printf("\n");
    }
    p1 = A.base;
    printf("A.base=\n");
    for (i = 0; i < bound1 * bound2 * bound3; i++) //顺序输出A.base
    {
        printf("%4d", *(p1 + i));
        if (i % (bound2 * bound3) == bound2 * bound3 - 1)
            printf("\n");
    }
    DestroyArray(&A);
    return 0;
}

运行结果1：

A.bounds=3 4 2
A.constants=8 2 1 
3页4行2列矩阵元素如下:
将 i*100+j*10+k赋值给A[i][j][k]:

A[0][0][0]= 0 A[0][0][1]= 1
A[0][1][0]=10 A[0][1][1]=11
A[0][2][0]=20 A[0][2][1]=21
A[0][3][0]=30 A[0][3][1]=31

A[1][0][0]=100 A[1][0][1]=101
A[1][1][0]=110 A[1][1][1]=111
A[1][2][0]=120 A[1][2][1]=121
A[1][3][0]=130 A[1][3][1]=131

A[2][0][0]=200 A[2][0][1]=201
A[2][1][0]=210 A[2][1][1]=211
A[2][2][0]=220 A[2][2][1]=221
A[2][3][0]=230 A[2][3][1]=231

A.base=
   0   1  10  11  20  21  30  31
 100 101 110 111 120 121 130 131
 200 201 210 211 220 221 230 231

运行结果2：

A.bounds=3 4 2
A.constants=8 2 1
3页4行2列矩阵元素如下:
将(i * 4 * 2 + j * 2 + k) * 4赋值给A[i][j][k]:

A[0][0][0]= 0 A[0][0][1]= 4
A[0][1][0]= 8 A[0][1][1]=12
A[0][2][0]=16 A[0][2][1]=20
A[0][3][0]=24 A[0][3][1]=28

A[1][0][0]=32 A[1][0][1]=36
A[1][1][0]=40 A[1][1][1]=44
A[1][2][0]=48 A[1][2][1]=52
A[1][3][0]=56 A[1][3][1]=60

A[2][0][0]=64 A[2][0][1]=68
A[2][1][0]=72 A[2][1][1]=76
A[2][2][0]=80 A[2][2][1]=84
A[2][3][0]=88 A[2][3][1]=92

A.base=
   0   4   8  12  16  20  24  28
  32  36  40  44  48  52  56  60
  64  68  72  76  80  84  88  92

三、矩阵的压缩存储

矩阵定义：一个由 m×n 个元素排成的 m 行（横向） n 列（纵向）的表。

对于值相同的元素很多且呈某种规律分布、零元素多的矩阵，为了节省存储空间，可以对这类矩阵进行压缩存储。

矩阵的压缩存储：

为多个相同的非零元素只分配一个存储空间
对零元素不分配空间

下面我们将会介绍特殊矩阵和稀疏矩阵的压缩存储。

3.1、特殊矩阵

3.1.1、对称矩阵

在一个 n 阶方阵 A 中，若元素满足下述性质： $a_{ij} = a_{ji}$ (1 ≤ i , j ≤ n )，则称 A 为对称矩阵。

对称矩阵上下三角中的元素数均为： n(n + 1) / 2

因此可以行序为主序将元素存放在一个一维数组 sa[n(n+1)/2] 中：

那么 $a_{ij}$ 和 sa[k] 中，如何根据 i 和 j 确定其对应的数组下标 k 呢？

解释：

【1】对于下三角形的行序存储： $a_{ij}$ 前的 i -1 行有 1+ 2 +…+ (i -1)= i(i -1)/2 个元素(求和)，在第 i 行上有 j 个元素。

【2】对于上三角形的列序存储： $a_{ij}$ 前的 j -1 列有 1+ 2 +…+ (i -1)= j(j -1)/2 个元素(求和)，在第 j 列上有 i 个元素。

⚠️注意：对于上三角的列序存储和下三角的行序存储，采用的分析方式是相同的。

对于上三角的行序存储的数组下标 k： $\frac{(i - 1) * (2n -(i - 2))}{2} + j -i$
对于下三角的列序存储的数组下标 k： $\frac{(j - 1) * (2n -(j - 2))}{2} + i -j$

因为 $a_{ij} = a_{ji}$ ，所以只要交换关系式中的 i 和 j 即可。

例题：

根据上面的公式，将 i = 6 , j = 7 代入得a67对于的下标k为：

[（6-1）* （2 * 8 - （6 - 2））] / 2 + (7 - 6) == 31

所以a67的地址为：1000 + 31 * 3 = 1093

当然这题的数据给的比较小，也可以不用公式：

这个元素在上三角部分中，是第6行中第2个元素，而这个元素的前面应该存储了31个元素(8+7+6+5+4+1=31)，又由于每个矩阵元素占3个单元，所以矩阵元素a67的地址为1000+31×3=1093。

3.1.2、三角矩阵

以主对角线划分，三角矩阵有上（下）三角两种。上（下）三角矩阵的下（上）三角（不含主对角线）中的元素均为常数。在大多数情况下，三角矩阵常数为零。

三角矩阵的存储：除了存储主对角线及上（下）三角中的元素外，再加一个存储常数 c 的空间。

3.1.3、对角矩阵（带状矩阵）

对角矩阵可按行优先顺序或对角线的顺序。都可将其压缩存储到一维数组中，且也能找到每个非零元素和向量下标的对应关系。

当然对于按对角线存储我们也可以采用一个二维数组来存，这也许比用一维数组顺序存储方便一点：

对于前者占用空间为：6 * 6 = 36，压缩后的空间占：5 * 6 = 30 ，虽然压缩的空间不是很多，但是当对角矩阵很大时，其压缩效果就比较显著了。

3.2、稀疏矩阵(超详细)

稀疏矩阵：设在 m×n 的矩阵中有 t 个非零元素。令 $\delta$ = t / (m × n) ，当 $\delta$ ≤0.05 时称为稀疏矩阵。

压缩存储原则：存各非零元的值、行列位置和矩阵的行列数。

三元组 $(i , j,a_{ij})$ 惟一确定矩阵的一个非零元，因此：

M 可以由 {(1,2,12), (1,3,9), (3,1,-3), (3,6,14), (4,3,24), (5,2,18), (6,1,15), (6,4,-7) } 和矩阵维数 (6, 7) 唯一确定。

⚠️通常，为了可靠描述，还会加一个总行数、总列数、非零元素总个数。

稀疏矩阵的压缩存储方法——顺序存储结构

#define MAXSIZE 12500 //假设非零元个数的最大值

typedef struct { 
    int i, j; //该非零元的行列下标
    Elemtype e; 
}Triple;

typedef struct { 
    Triple data[MAXSIZE + 1]; 
    int mu, nu, tu; //矩阵的总行、总列数和总非零元个数
}TSMatrix;

扩展：已知一个稀疏矩阵的三元组表，求该矩阵转置矩阵的三元组表。

转置矩阵：一个 m×n 的矩阵 M，它的转置 T 是一个 n×m 的矩阵，且 T (i, j) = M[ j, i]，1≤i≤n，1≤j≤m，即 M 的行是 T 的列，M 的列是 T 的行。

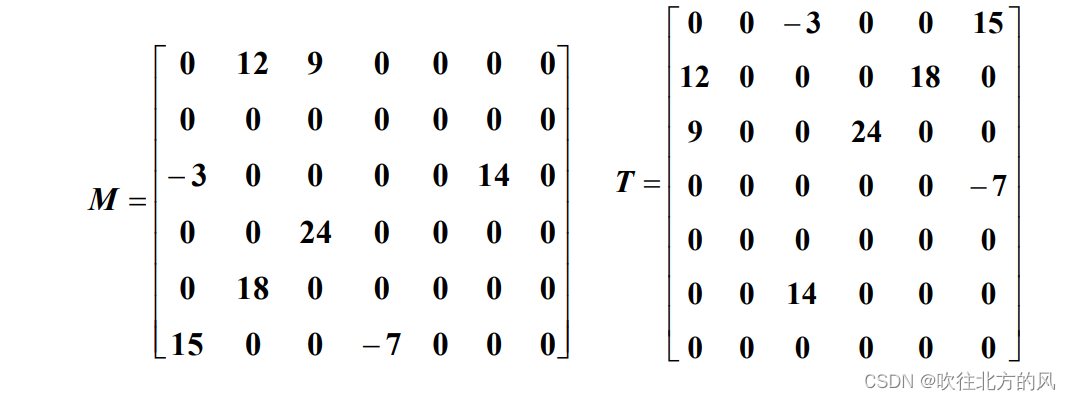
法一：

代码实现：

Status TransposeSMatrix(TSMatrix M, TSMatrix &T) { 
    T.mu=M.nu; T.nu=M.mu; T.tu=M.tu; 
    int q = 1;
    if (T.tu) 
   { 
    for (int col = 1; col <= M.nu; ++ col) //nu是M的列
     {
    	 for (int p = 1; p <= M.tu; ++ p) { //tu是M对应的三元组非零元总数
    	 	if ( M.data[p].j == col ) {
    	 		T.data[q].i = M.data[p].j ; 
                T.data[q].j = M.data[p].i ; 
                T.data[q].e = M.data[p].e ;
                q++;
			 }
		 }
	 }
  }
  return OK; 
} // TransposeSMatrix

时间复杂度：O(nu * tu) ，若 tu 与mu * nu 同数量级，则为：O(mu* $nu^{2}$ )

三元组的快速转置算法：

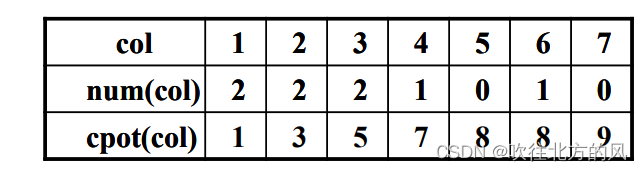
上面那张图，是实现三元组快速转置前，必须需要求得的数据，下面就分别介绍它们的求法：

【1】num[col]的由来：

【2】cpot[col] 的由来（借助num[col]）:

理解了上面两个数组的求解，下面就开始如何通过 cpot[col] 数组，准确找到转置矩阵T的三元组的每一行应该存哪一个非零元数：

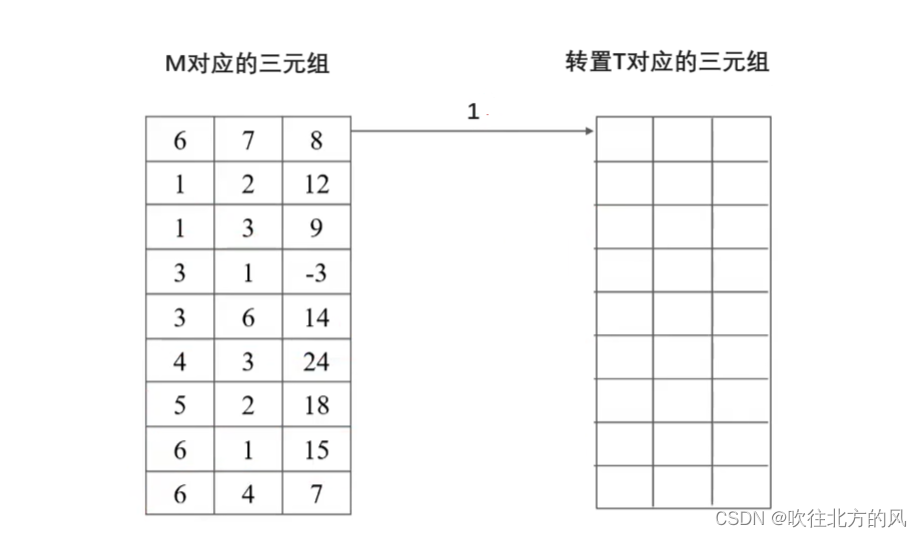
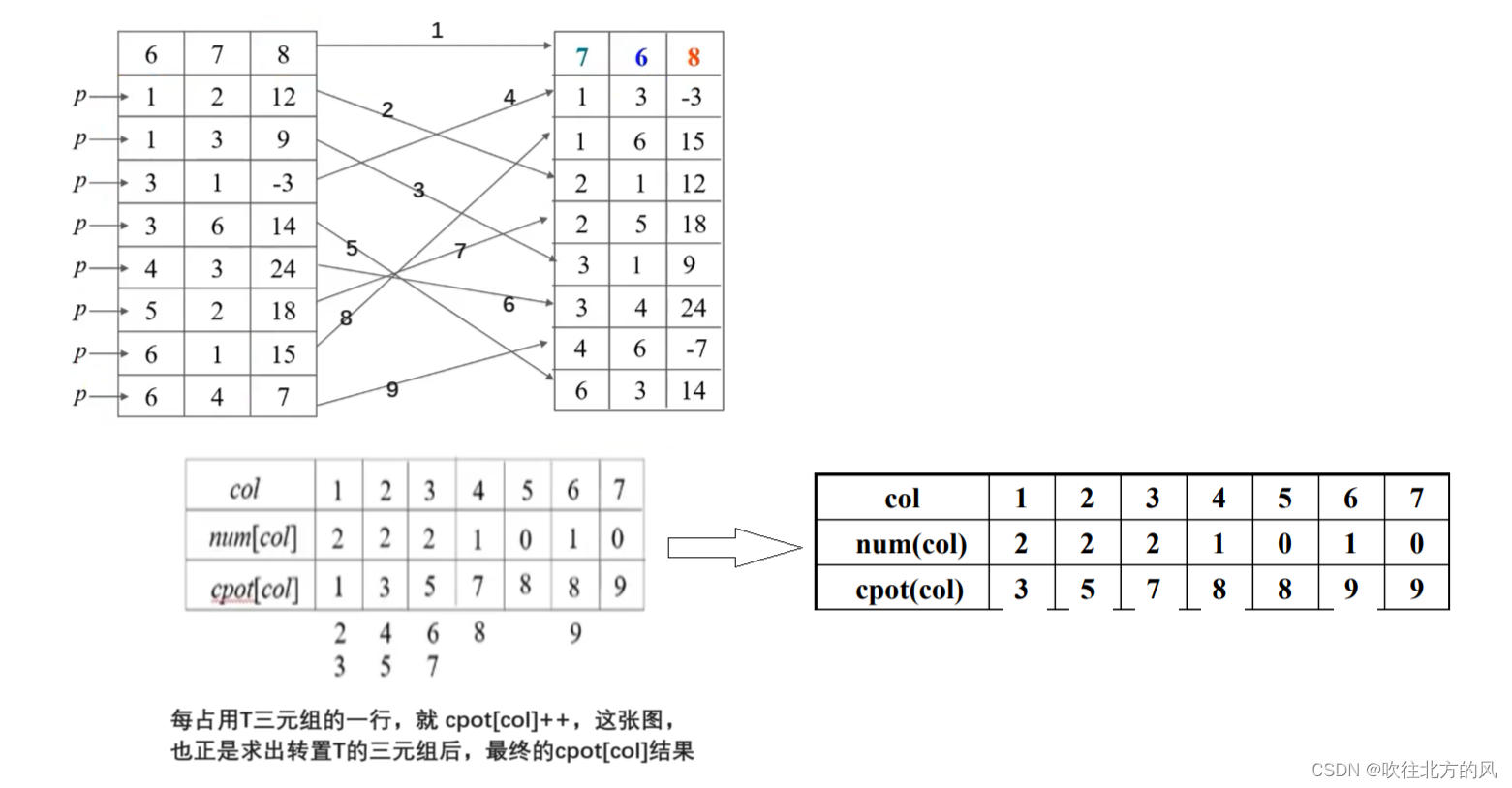
完整代码：

Status FastTransposeSMatrix( TSMatrix M, TSMatrix &T ,int num[] , int cpot[]) { 
// 采用三元组顺序表存储表示，求稀疏矩阵 M 的转置矩阵 T 
    T.mu = M.nu; T.nu = M.mu; T.tu = M.tu; 
    if (T.tu) { 
        for (int col=1; col<=M.nu; ++col) num[col] = 0; 
        for (int t = 1; t <= M.tu ; ++t) ++num[M.data[t].j]; // 求 M 中各列非零元的个数
        
        cpot[1] = 1;
        for (int col = 2; col <= M.nu ; ++col) cpot[col] = cpot[col -1] + num[col -1]; // 求 M 中各列的第一个非零元在 T.data 中的序号

        int col , q;
        for (int p = 1 ; p <= M.tu ; ++p) { // 开始求 M的转置 T对应的三元组
             col = M.data[p].j;
			 q = cpot[col]; 
             T.data[q].i = M.data[p].j; T.data[q].j = M.data[p].i; 
             T.data[q].e = M.data[p].e; 
			 cpot[col]++; 
            } 
   } 
   return OK;
} // FastTransposeSMatri

上面代码时间复杂度：O(nu + tu) ，若 tu 与 mu * nu 同数量级，则为：O(mu * nu)

优缺点：

三元组顺序表又称有序的双下标法。

三元组顺序表的优点：非零元在表中按行序有序存储，因此便于进行依行顺序处理的矩阵运算。

三元组顺序表的缺点：不能随机存取。若按行号存取某一行中的非零元，则需从头开始进行查找。

3.3、十字链表（稀疏矩阵的链式存储结构）

正如三元组顺序表的缺点所在，我们可以用稀疏矩阵的链式存储结构来解决这个问题。

优点：它能够灵活地插入因运算而产生的新的非零元素，删除因运算而产生的新的零元素，实现矩阵的运算。

在十字链表中，矩阵的每一个非零元素用一个结点表示，该结点除了（row，col，value）外，还有两个域：

right：用于链接同一行中的下一个非零元素；
down：用以链接同一列中的下一个非零元素。

十字链表中结点的结构示意图：

这里看两个稀疏矩阵的存储示意图，你大概就能明白他的大致结构了：

【1】

【2】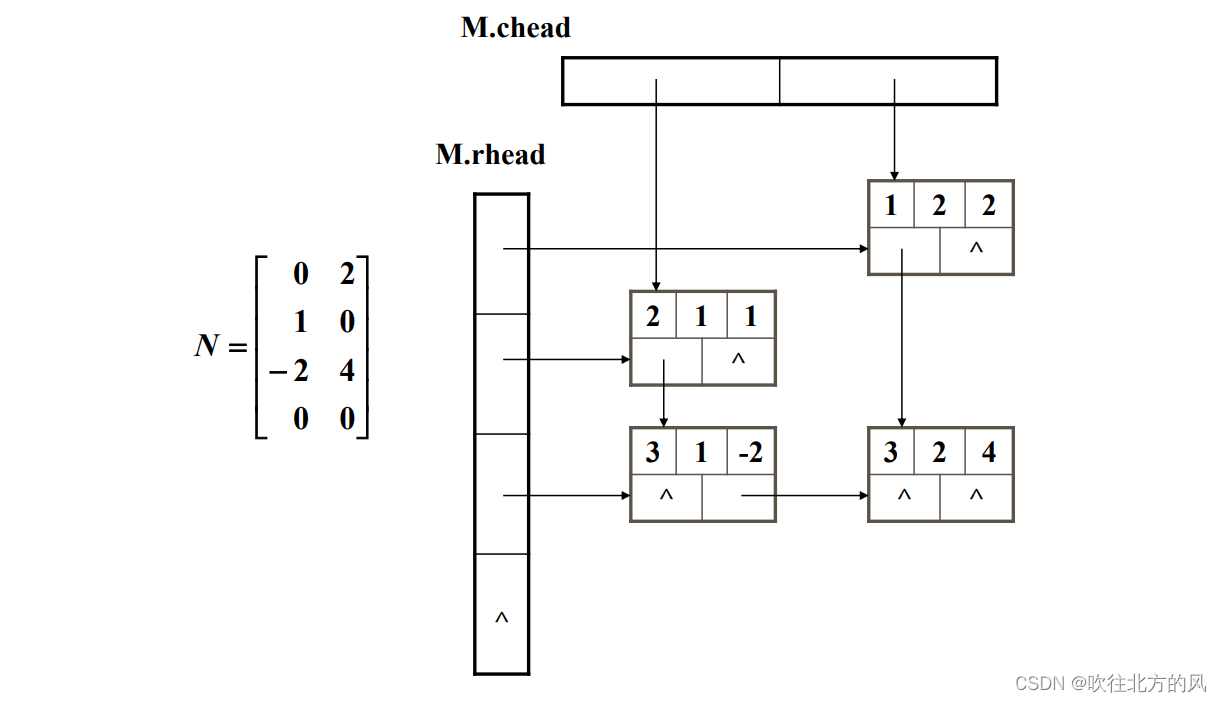

十字链表的结构类型说明如下：

typedef struct OLNode
{ 
   int i, j; // 非零元素的行和列下标
   ElemType e;
   struct OLNode * right, *down; // 非零元素所在行表、列表的后继链域
} OLNode; *OLink;

typedef struct
{ 
   OLink * rhead , *chead; //行、列链表的头指针向量基址，注意这里是指针数组（即OLNode结构的结点的指针的指针）
   int mu, nu, tu; //稀疏矩阵的行数、列数、非零元个数
} CrossList;

这里的结构和上一章讲【数据结构复习之路】栈和队列（本站最全最详细讲解）& 严蔚敏版-CSDN博客

里面的队列的链式存储是非常相似的，只是这里的每一行、每一列都是可以看成一个链队列。

下面给出可运行的完整代码（三元组转十字链表），希望能帮助你理解：

#include<stdio.h>
#include<stdlib.h>
typedef struct OLNode
{
    int i, j, e; //矩阵三元组i代表行 j代表列 e代表当前位置的数据
    struct OLNode* right, * down; //指针域 右指针 下指针
}OLNode, * OLink;
typedef struct
{
    OLink* rhead, * chead; //行和列链表头指针
    int mu, nu, tu;  //矩阵的行数,列数和非零元的个数
}CrossList;
void CreateMatrix_OL(CrossList* M);
void display(CrossList M);
int main()
{
    CrossList M;
    M.rhead = NULL;
    M.chead = NULL;
    CreateMatrix_OL(&M);
    printf("输出矩阵M:\n");
    display(M);
    return 0;
}
void CreateMatrix_OL(CrossList* M)
{
    int m, n, t;
    int num = 0;
    int i, j, e;
    OLNode* p = NULL, * q = NULL;
    printf("输入矩阵的行数、列数和非0元素个数：");
    scanf("%d%d%d", &m, &n, &t);
    (*M).mu = m;
    (*M).nu = n;
    (*M).tu = t;
    if (!((*M).rhead = (OLink*)malloc((m + 1) * sizeof(OLink))) || !((*M).chead = (OLink*)malloc((n + 1) * sizeof(OLink))))
    {
        printf("初始化矩阵失败");
        exit(0);
    }
   
    for (i = 0; i <= m; i++)
    {
        (*M).rhead[i] = NULL;
    }
    for (j = 0; j <= n; j++)
    {
        (*M).chead[j] = NULL;
    }
    while (num < t) {
        scanf("%d%d%d", &i, &j, &e);
        num++;
        if (!(p = (OLNode*)malloc(sizeof(OLNode))))
        {
            printf("初始化三元组失败");
            exit(0);
        }
        p->i = i;
        p->j = j;
        p->e = e;
        //链接到行的指定位置
        //如果第 i 行没有非 0 元素，或者第 i 行首个非 0 元素位于当前元素的右侧，直接将该元素放置到第 i 行的开头
        if (NULL == (*M).rhead[i] || (*M).rhead[i]->j > j)
        {
            p->right = (*M).rhead[i];
            (*M).rhead[i] = p;
        }
        else
        {
            //找到当前元素的位置
            for (q = (*M).rhead[i]; (q->right) && q->right->j < j; q = q->right);
            //将新非 0 元素插入 q 之后
            p->right = q->right;
            q->right = p;
        }
        //链接到列的指定位置
        //如果第 j 列没有非 0 元素，或者第 j 列首个非 0 元素位于当前元素的下方，直接将该元素放置到第 j 列的开头
        if (NULL == (*M).chead[j] || (*M).chead[j]->i > i)
        {
            p->down = (*M).chead[j];
            (*M).chead[j] = p;
        }
        else
        {
            //找到当前元素要插入的位置
            for (q = (*M).chead[j]; (q->down) && q->down->i < i; q = q->down);
            //将当前元素插入到 q 指针下方
            p->down = q->down;
            q->down = p;
        }
    }
}
void display(CrossList M) {
    int i,j;
    //一行一行的输出
    for (i = 1; i <= M.mu; i++) {
        //如果当前行没有非 0 元素，直接输出 0
        if (NULL == M.rhead[i]) {
            for (j = 1; j <= M.nu; j++) {
                printf("0 ");
            }
            putchar('\n');
        }
        else
        {
            int n = 1;
            OLink p = M.rhead[i];
            //依次输出每一列的元素
            while (n <= M.nu) {
                if (!p || (n < p->j) ) {
                    printf("0 ");
                }
                else
                {
                    printf("%d ", p->e);
                    p = p->right;
                }
                n++;
            }
            putchar('\n');
        } 
    }
}

输出结果：

输入矩阵的行数、列数和非0元素个数：3 4 4
1 1 3
1 4 5
2 2 -1
3 1 2
输出矩阵M:
3 0 0 5
0 -1 0 0
2 0 0 0

四、广义表的定义

广义表（又称列表 Lists）是 n≥0个元素 a1 , a2 , …, an 的有限序列，其中每一个ai 或者是原子（单个元素），或者是一个子表。

广义表通常记作： LS = (a1，a2，…，an )

其中： LS 为表名， n 为表的长度，每一个 ai 为表的元素。习惯上，一般用大写字母表示广义表，小写字母表示原子。

表头：若 LS 非空 (n≥1 )，则其第一个元素 a1 就是表头。记作 head(LS) = a1。
注：表头可是原子，也可是子表。
表尾：除表头之外的其它元素组成的表。记作 tail(LS) = (a2 , ..., an )。
注：表尾不是最后一个元素，而是一个子表。

【例题】

A=( ) ：空表，长度为 0
B=(( )) ：长度为 1，表头、表尾均为 ( )
C=(a, (b, c)) ：长度为 2，由原子 a 和子表 (b, c) 构成，表头为 a ；表尾为 ((b, c))
D=(x,y,z)：长度为 3，每一项都是原子，表头为 x ；表尾为 (y, z)
E=(C, D)：长度为 2，每一项都是子表。表头为 C ；表尾为 (D)
F=(a, F)：长度为 2，第一项为原子，第二项为它本身（F），表头为 a ；表尾为 (F)

4.1、广义表的性质

【1】广义表中的数据元素有相对次序（一个直接前驱和一个直接后继【除了表头和表尾】）

【2】广义表的长度定义为最外层所包含元素的个数；如： C=(a, (b, c)) 是长度为 2 的广义表。

【3】广义表的深度定义为该广义表展开后所含括号的重数。e.g： A = (b, c) 的深度为 1，B = (A, d) 的深度为 2， C = (f, B, h) 的深度为 3。

⚠️注意：“原子”的深度为 0 ; “空表”的深度为 1 。

【4】广义表可以为其他广义表共享；如：广义表 B 就共享表 A。在 B 中不必列出 A 的值，而是通过名称来引用。

【5】广义表可以是递归的表。如：F=(a, F)=(a, (a, (a, …))) ，注意：递归表的深度是无穷值，长度是有限值。

【6】广义表是多层次结构，广义表的元素可以是单元素，也可以是子表，而子表的元素还可以是子表，…。可以用图形象地表示。

广义表可看成是线性表的推广，线性表是广义表的特例。

广义表的结构相当灵活，在某种前提下，它可以兼容线性表、数组、树和有向图等各种常用的数据结构。

当二维数组的每行（或每列）作为子表处理时，二维数组即为一个广义表。

另外，树和有向图也可以用广义表来表示。由于广义表不仅集中了线性表、数组、树和有向图等常见数据结构的特点，而且可有效地利用存储空间，因此在计算机的许多应用领域都有成功使用广义表的实例

广义表基本运算：

取表头运算 GetHead 和取表尾运算 GetTail

若广义表 LS=(a1 , a2 , …, an )，则 GetHead(LS) = a1 ， GetTail(LS) = (a2 , …, an )。

⚠️注意：取表头得到的结果可以是原子，也可以是一个子表。取表尾得到的结果一定是一个子表。

e.g: D = ( E, F ) = ((a, (b, c))，F )

GetHead( D ) = E ，GetTail( D ) = ( F )
GetHead( E ) = a ，GetTail( E ) = ((b, c))
GetHead(((b, c))) = (b, c) ，GetTail(((b, c))) = ( )
GetHead((b, c)) = b ，GetTail((b, c)) = (c)
GetHead((c)) = c ，GetTail((c)) = ( )

4.2、广义表的存储结构

由于广义表中既可存储原子（不可再分的数据元素），也可以存储子表，因此很难使用顺序存储结构表示，通常情况下广义表结构采用链表实现。

比如D = (a , ((b , c) , d) ) ，如果采用顺序存储，就需要一个三维数组，这是非常浪费存储空间的！

4.2.1、链表表示（法1）

法1也叫：头尾链表存储

typedef struct GLNode {
    int tag;//标志域，用于区分元素结点和表结点

    union {  //元素结点和表结点的联合部分
        char atom;//atom是原子结点的值域
        struct {
            struct GLNode* hp, * tp;
        }ptr;//ptr是表结点的指针域，hp指向表头；tp指向表尾
    }un;
}GLNode, * Glist;

这里用到了 union 共用体，因为同一时间此节点不是原子节点就是子表节点，当表示原子节点时，就使用 atom 变量；反之则使用 ptr 结构体。

这里我用法1链表存储该广义表，并画出了图，你能看出哪些特点呢？

【1】

【2】

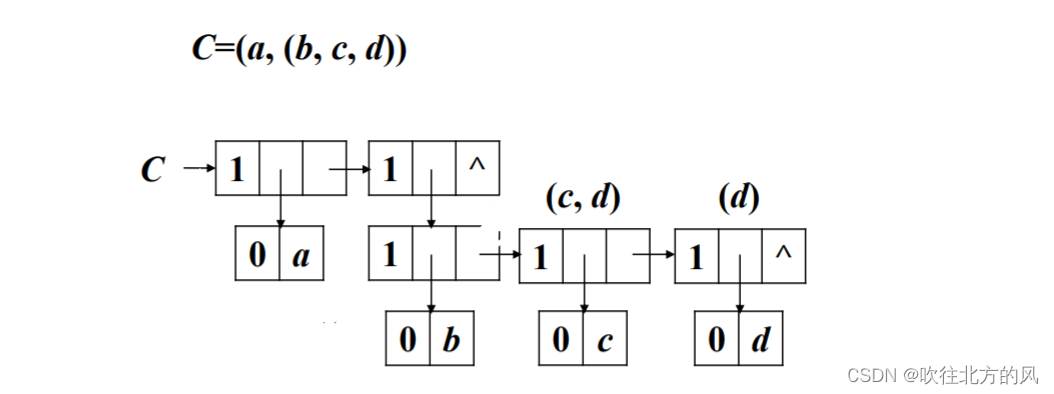
【3】

【4】

【总结】

从图【2】可以看到，存储原子 a、b、c、d 时都是用子表包裹着表示的，因为原子 a 和子表 (b,c,d) 在广义表中同属一级，而原子 b、c、d 也同属一级。
就如A，除非A是一个空表，指针A的值为 NULL，否则指针A的指向的一定是 tag 值为 1 的子表结点。
采用首尾表示法容易分清列表中原子或子表所在的层次
最高层的表结点的个数即为广义表的长度

这里给出这种结构，求广义表长度的完整代码：

假设 C = （a , ( b , c , d )）

#include <stdio.h>
#include <stdlib.h>
typedef struct GLNode{
    int tag;//标志域
    union{
        char atom;//原子结点的值域
        struct{
            struct GLNode * hp,*tp;
        }ptr;//子表结点的指针域，hp指向表头；tp指向表尾
    };
}*Glist;
Glist creatGlist(Glist C){
    //广义表C
    C=(Glist)malloc(sizeof(Glist));
    C->tag=1;
    //表头原子‘a’
    C->ptr.hp=(Glist)malloc(sizeof(Glist));
    C->ptr.hp->tag=0;
    C->ptr.hp->atom='a';
    //表尾子表（b,c,d）,是一个整体
    C->ptr.tp=(Glist)malloc(sizeof(Glist));
    C->ptr.tp->tag=1;
    C->ptr.tp->ptr.hp=(Glist)malloc(sizeof(Glist));
    C->ptr.tp->ptr.tp=NULL;
    //开始存放下一个数据元素（b,c,d）,表头为‘b’，表尾为（c,d）
    C->ptr.tp->ptr.hp->tag=1;
    C->ptr.tp->ptr.hp->ptr.hp=(Glist)malloc(sizeof(Glist));
    C->ptr.tp->ptr.hp->ptr.hp->tag=0;
    C->ptr.tp->ptr.hp->ptr.hp->atom='b';
    C->ptr.tp->ptr.hp->ptr.tp=(Glist)malloc(sizeof(Glist));
    //存放子表(c,d)，表头为c，表尾为d
    C->ptr.tp->ptr.hp->ptr.tp->tag=1;
    C->ptr.tp->ptr.hp->ptr.tp->ptr.hp=(Glist)malloc(sizeof(Glist));
    C->ptr.tp->ptr.hp->ptr.tp->ptr.hp->tag=0;
    C->ptr.tp->ptr.hp->ptr.tp->ptr.hp->atom='c';
    C->ptr.tp->ptr.hp->ptr.tp->ptr.tp=(Glist)malloc(sizeof(Glist));
    //存放表尾d
    C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->tag=1;
    C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.hp=(Glist)malloc(sizeof(Glist));
    C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.hp->tag=0;
    C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.hp->atom='d';
    C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.tp=NULL;
    return C;
}
int GlistLength(Glist C){
    int Number=0;
    Glist P=C;
    while(P){
        Number++;
        P=P->ptr.tp;
    }
    return Number;
}
int main(){
    Glist C = creatGlist(C);
    printf("广义表的长度为：%d",GlistLength(C));
    return 0;
}

输出结果为：

广义表的长度为：2

4.2.2、链表表示（法2）

法2也叫：扩展线性链表存储（孩子兄弟链表）

typedef struct GLNode {
    int tag;// 标志域，用于区分元素结点和表结点

    union {  // 元素结点和表结点的联合部分
        char atom;//原子结点的值域
        struct GLNode* hp;//表结点的表头指针
    }un;
    struct GLNode* tp;//这里的tp相当于链表的next指针，用于指向下一个数据元素
}GLNode, * GList;

这里我用法2链表存储该广义表，并画出了图，你能看出哪些特点呢？

【1】

【2】

【3】

【4】

【总结】

无论 A 是否为空表，指针 A 指向的都是一个 tag 值为 1 的子表结点。当 A 为空表时，指针 A 所指结点的 hp 和 tp 指针都为 NULL。
最高层结点 tp 域必为 NULL
表达式中的左括号 “（ ” 对应存储表示中的 tag = 1 的结点。
就如【图2】，由于其最顶层（蓝色标注）表示的此广义表，而第二层（红色标注）表示的才是该广义表中包含的数据元素，因此可以通过计算第二层中包含的节点数量，才可求得广义表的长度。

选择一个自己更擅长的结构就行了，我更倾向于法1的存储结构。

4.3、广义表的深度递归算法

思路：

依次遍历广义表 C 的每个节点，若当前节点为原子（tag 值为 0），则返回 0；若为空表，则返回 1；反之，则继续遍历该子表中的数据元素。
设置一个初始值为 0 的整形变量 max，每次递归过程返回时，令 max 与返回值进行比较，并取较大值。这样，当整个广义表递归结束时，max+1 就是广义表的深度。
其实，每次递归返回的值都是当前所在的子表的深度，原子默认深度为 0，空表默认深度为 1。

基于法1的存储结构：

#include <stdio.h>
#include <stdlib.h>
 
typedef struct GLNode{
    int tag;//标志域
    union{
        char atom;//原子结点的值域
        struct{
            struct GLNode * hp,*tp;
        }ptr;//子表结点的指针域，hp指向表头；tp指向表尾
    };
}*Glist,GNode;
 
Glist creatGlist(Glist C){
    //广义表C
    C=(Glist)malloc(sizeof(GNode));
    C->tag=1;
    //表头原子‘a’
    C->ptr.hp=(Glist)malloc(sizeof(GNode));
    C->ptr.hp->tag=0;
    C->ptr.hp->atom='a';
    //表尾子表（b,c,d）,是一个整体
    C->ptr.tp=(Glist)malloc(sizeof(GNode));
    C->ptr.tp->tag=1;
    C->ptr.tp->ptr.hp=(Glist)malloc(sizeof(GNode));
    C->ptr.tp->ptr.tp=NULL;
    //开始存放下一个数据元素（b,c,d）,表头为‘b’，表尾为（c,d）
    C->ptr.tp->ptr.hp->tag=1;
    C->ptr.tp->ptr.hp->ptr.hp=(Glist)malloc(sizeof(GNode));
    C->ptr.tp->ptr.hp->ptr.hp->tag=0;
    C->ptr.tp->ptr.hp->ptr.hp->atom='b';
    C->ptr.tp->ptr.hp->ptr.tp=(Glist)malloc(sizeof(GNode));
    //存放子表(c,d)，表头为c，表尾为d
    C->ptr.tp->ptr.hp->ptr.tp->tag=1;
    C->ptr.tp->ptr.hp->ptr.tp->ptr.hp=(Glist)malloc(sizeof(GNode));
    C->ptr.tp->ptr.hp->ptr.tp->ptr.hp->tag=0;
    C->ptr.tp->ptr.hp->ptr.tp->ptr.hp->atom='c';
    C->ptr.tp->ptr.hp->ptr.tp->ptr.tp=(Glist)malloc(sizeof(GNode));
    //存放表尾d
    C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->tag=1;
    C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.hp=(Glist)malloc(sizeof(GNode));
    C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.hp->tag=0;
    C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.hp->atom='d';
    C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.tp=NULL;
    return C;
}
int GlistDepth(Glist C){
    //如果表C为空表时，直接返回长度1；
    if (!C) {
        return 1;
    }
    //如果表C为原子时，直接返回0；
    if (C->tag==0) {
        return 0;
    }
    int max=0;//设置表C的初始长度为0；
    for (Glist pp=C; pp; pp=pp->ptr.tp) {
        int dep=GlistDepth(pp->ptr.hp); //求以 pp -> ptr.hp为头指针的子表深度 
        if (dep>max) {
            max=dep;//每次找到表中遍历到深度最大的表，并用max记录
        }
    }
    //程序运行至此处，表明广义表不是空表，由于原子返回的是0，而实际长度是1，所以，此处要+1；
    return max+1;
}
int main(int argc, const char * argv[]) {
    Glist C=creatGlist(C);
    printf("广义表的深度为：%d",GlistDepth(C));
    return 0;
}

输出结果为：