完整代码:
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Title</title>
<style type="text/css">
#box1 table{
border: 0px;
border-collapse: collapse;
cursor: pointer;
background-color: gray;
}
#box1 th {
border: 0px;
border-collapse: collapse;
cursor: pointer;
}
#box1 td{
border: 1px solid #000;
border-collapse: collapse;
cursor: pointer;
text-align: center;
font-size: 4;
}
#box1{
border: 0px;
}
.wall{
background-color: black;
}
.startPoint{
background-color: blue;
}
.targetPoint{
background-color: blue;
}
.passed{
background-color: yellow;
}
</style>
</head>
<body>
单击灰色格子将其设置为障碍( 黑色 ),单击障碍清空障碍
<div id="box1"></div>
<button onclick="startSearch()">开始寻路</button>
<button onclick="initRingWalls()">生成环状障碍</button>
<button onclick="initPointWalls()">生成点状障碍</button>
</body>
<script type="text/javascript">
var map_code_td = new Map();
var row_count = 40;
var col_count = 40;
var rowNum_start = 1;
var colNum_start = 1;
var rowNum_target = 20;
var colNum_target = 20;
var map_code_wallYn = new Map();
var code_start = rowNum_start + "_" + colNum_start;
var code_target = rowNum_target + "_" + colNum_target;
// 辅助帮助显示横竖纹的底色棋盘,没有任何事件和业务逻辑
function initBox1( ) {
var table = document.createElement("table");
table.rules = 'all' ;
for (var rowNum = 1; rowNum <= row_count; rowNum++) {
var tr = document.createElement("tr");
for (var colNum = 1; colNum <= col_count; colNum++) {
var td = document.createElement("td");
td.width = 10;
td.height = 10;
td.className ="road";
tr.appendChild(td);
var code = rowNum + "_" + colNum;
map_code_td.set(code, td);
}
table.appendChild(tr);
}
document.getElementById( "box1" ).appendChild(table);
table.addEventListener( "click", setOrClearWall );
var code_start = rowNum_start + "_" + colNum_start;
var code_target = rowNum_target + "_" + colNum_target;
map_code_td.get( code_start ).className = "startPoint";
map_code_td.get( code_target ).className = "targetPoint";
}
function initPointWalls(){
// 清空障碍
clearAllWalls();
for (var rowNum = 1; rowNum <= row_count; rowNum++) {
for (var colNum = 1; colNum <= col_count; colNum++) {
var code = rowNum + "_" + colNum;
if( code == code_start || code == code_target ){
continue;
}
// 右 1/3 的几率成为障碍
var randomNum = randomBetween(1,10000);
if( randomNum < 3333 ){
var td = map_code_td.get( code );
td.className = "wall";
map_code_wallYn.set( code, 'y' );
}
}
}
}
// 鼠标的点击事件监听方法,用来将点击的格子设置为墙
function setOrClearWall(){
var td = event.srcElement;
var rowNum = td.parentElement.rowIndex + 1;
var colNum = td.cellIndex + 1;
var code = rowNum + "_" + colNum;
if( td.className == "wall" ){
td.className = "road";
map_code_wallYn.set( code, "n" );
}else if( td.className =='road' ){
td.className = "wall";
map_code_wallYn.set( code, "y" );
}
}
function randomBetween(minNum,maxNum){
return Math.floor(Math.random() * (maxNum - minNum + 1)) + minNum;
}
function clearAllWalls(){
for (var rowNum = 1; rowNum <= row_count; rowNum++) {
for (var colNum = 1; colNum <= col_count; colNum++) {
var code = rowNum + "_" + colNum;
if( code == code_start || code == code_target){
continue;
}
var wallYn = map_code_wallYn.get( code );
if( wallYn == 'y' ){
map_code_td.get( code ).className = "";
map_code_wallYn.set( code, "n" );
}else{
var td = map_code_td.get( code );
if( td.className == 'passed' ){
td.className = "";
}
}
}
}
}
function initRingWalls(){
// 清空障碍
clearAllWalls();
// 将第三行设置为障碍
var circles = [2,4,6,8,10,12,14,16,18];
for( var i in circles ){
var circle = circles[i];
var randomNum = randomBetween(1,4);
var randomNum_1 = randomBetween(circle,col_count - circle);
var randomNum_2 = randomBetween(circle,col_count - circle);
var randomNum_3 = randomBetween(circle,row_count - circle);
var randomNum_4 = randomBetween(circle,row_count - circle);
// 顶行
for (var colNum = circle; colNum <= ( col_count - circle );colNum++){
if( randomNum == 1 ){
if( colNum == randomNum_1 ){
continue;
}
}
var code = circle + "_" + colNum;
map_code_td.get( code ).className = "wall";
map_code_wallYn.set( code, "y" );
}
// 底行
for (var colNum = circle; colNum <= ( col_count - circle );colNum++){
if( randomNum == 2 ){
if( colNum == randomNum_2 ){
continue;
}
}
var code = ( row_count - circle ) + "_" + colNum;
map_code_td.get( code ).className = "wall";
map_code_wallYn.set( code, "y" );
}
// 左列
for (var rowNum = circle; rowNum <= ( row_count - circle );rowNum++){
if( randomNum == 3 ){
if( rowNum == randomNum_3 ){
continue;
}
}
var code = rowNum + "_" + circle;
map_code_td.get( code ).className = "wall";
map_code_wallYn.set( code, "y" );
}
// 右列
for (var rowNum = circle; rowNum <= ( row_count - circle );rowNum++){
if( randomNum == 4 ){
if( rowNum == randomNum_4 ){
continue;
}
}
var code = rowNum + "_" + ( col_count - circle );
map_code_td.get( code ).className = "wall";
map_code_wallYn.set( code, "y" );
}
}
}
// 检测 code 表示的格子是否可以通行
function canPass( code ){
var arr = code.split("_");
var rowNum = parseInt( arr[0])
var colNum = parseInt( arr[1] );
if( rowNum > row_count || rowNum < 1 || colNum > col_count || colNum < 1 ){
// 该位置已经超过边界了,不能走
return false;
}
var wallYn = map_code_wallYn.get( code );
if( wallYn == 'y' ){
// 该位置是墙,不能走
return false;
}
return true;
}
class Node {
constructor(code,parent) {
this.code = code;
this.children = [];
this.parent = parent;
}
addChild(node) {
this.children.push(node);
}
}
initBox1( );
function startSearch( ){
// todo
var node_start = new Node( code_start,null )
console.log( node_start)
console.log( node_start.code)
var nodes_currLevel = [node_start];
var nodes_nextLevel = [];
var codes_passed = [];
var node_target = null;
while( true ){
// todo 如果找到了 目标节点或者 nodes_currLevel 为空了,需要退出循环
// todo 遍历 nodes_currLevel 中的 每个 node,检测其是否是目标节点,如果是目标节点,则找到了最短路径,
if( nodes_currLevel.length == 0 ){
break;
}
for( var i in nodes_currLevel ){
var node = nodes_currLevel[i];
console.log( "node = ",node)
var code = node.code;
console.log( "code = " + code );
if( codes_passed.indexOf( code ) > -1 ){
// 该节点已经遍历过了,不需要重复遍历
continue;
}
if( code == code_target ){
// 找到目标节点了
node_target = node;
break
}
// todo 找到该节点的所有可达子节点,保存到下一级的集合中,并将当前节点置为已遍历状态
// todo 找到该节点的上、右、下、左节点( 需要排除超过边界的和是障碍物的 )
var arr = code.split("_");
var rowNum = parseInt( arr[0] );
var colNum = parseInt( arr[1] );
var code_up = ( rowNum - 1 ) + "_" + colNum;
var code_right = rowNum + "_" + ( colNum + 1 );
var code_down = ( rowNum + 1 ) + "_" + colNum;
var code_left = rowNum + "_" + ( colNum - 1 );
if( canPass( code_up ) ){
// 上子节点可通过
// 更新树结构
var node_up = new Node( code_up,node );
node.addChild( node_up );
nodes_nextLevel.push( node_up );
}
if( canPass( code_right ) ){
// 右子节点可通过
// 更新树结构
var node_right = new Node( code_right,node );
node.addChild( node_right );
nodes_nextLevel.push( node_right );
}
if( canPass( code_down ) ){
// 下子节点可通过
// 更新树结构
var node_down = new Node( code_down,node );
node.addChild( node_down );
nodes_nextLevel.push( node_down );
}
if( canPass( code_left ) ){
// 左子节点可通过
// 更新树结构
var node_left = new Node( code_left,node );
node.addChild( node_left );
nodes_nextLevel.push( node_left );
}
codes_passed.push( code );
}
// 该层遍历完了,更新 nodes_currLevel 和重置 nodes_nextLevel
nodes_currLevel = nodes_nextLevel;
nodes_nextLevel = [];
if( node_target != null ){
break;
}
}
if( node_target != null ){
console.log("找到最短路径了,node_target = ",node_target);
// todo 画出最短路径
printPath( node_target );
}else{
alert( "未找到最短路径" );
}
}
function printPath( node_target ){
if( node_target == null ){
return;
}
var node_prev = node_target.parent;
console.log("node_prev = ",node_prev);
while( true ){
if( node_prev == null ){
break;
}
var code = node_prev.code;
if( code == code_start ){
break
}
var td = map_code_td.get( code );
td.className = "passed";
node_prev = node_prev.parent;
}
}
</script>
</html>

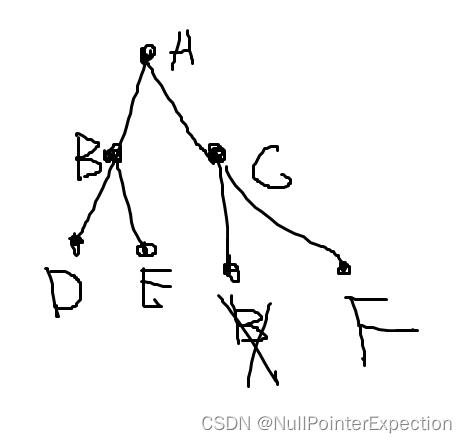
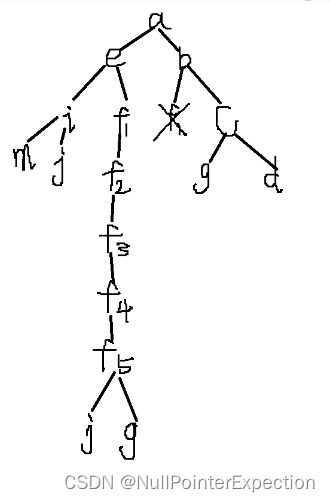
广度优先搜索算法求解最短路径的过程就是在构筑一棵多叉树,当找到表示目标节点的叶子节点时,显而易见该叶子节点到根节点( 开始节点 )的高度即是路径的长度,所以哪个叶子节点最先被发现是目标节点,显然该节点距离根节点的高度肯定是最短的,因为最先结束嘛,但是这也是广度优先搜索算法的局限性,就是要求任意两个连通节点之间的距离相等,如果这里A到B,A到C,B到D,C到F等的距离不是相等的,显然算法执行过程中最先搜到目标节点距离根节点的距离不一定是最短的,所以需要改进一下该算法,怎么改进呢?其实大名鼎鼎的 Dijkstra 迪杰斯特拉算法就是改进的广度优先搜索算法,不过迪杰斯特拉算法不是那么显而易见,即不是显而易见的傻瓜式的就能想到的,需要思考一下逻辑。其实我们可以换一种思维,在n*m网格中做文章,比如网格中的一个 code = "3_4"的格子( 即第3行第4列的格子 ),其距离为5 ,我们可以把它拆分成5个虚拟格子,code 分别为 "3_4_1"、 "3_4_2"、 "3_4_3"、 "3_4_4"、 "3_4_5",正常的一个格子,不考虑障碍物、边界、已经走完的格子,是有4个可达格子的,分别是其上、右、下、左边的格子,对于虚拟出的格子,它的可达格子只能是下一个虚拟格子( 当然对于最尾部的虚拟格子,它的可达格子和正常的格子是一样的,都是上右下左 ),如图:

a为起点,k为终点,f格子的距离为5,其余格子的距离都为1,带了虚拟格子的搜索树长如下这样: