对于代数Riccati方程的求解网上能找到很多的资源，matlab也有成熟的函数，但是对于时变系统的Riccati矩阵微分方程，能找到的资料还比较少。

一、求解代数Riccati方程

可以在网上找到很多资料，如

• https://blog.csdn.net/m0_62299908/article/details/127807014

matlab也有相应的一系列函数 lqr、icare等。
对于这些函数不同的适用范围自己目前了解的还不够，之后补上。
这些函数到底能不能用于求解时变系统自己还没搞清楚。

二、如何处理时变系统

参见matlab官方论坛 Solving Riccati differential equation with time variable matrix
这个帖子给出的方案是ode45中有一个关于处理时变项的例子。

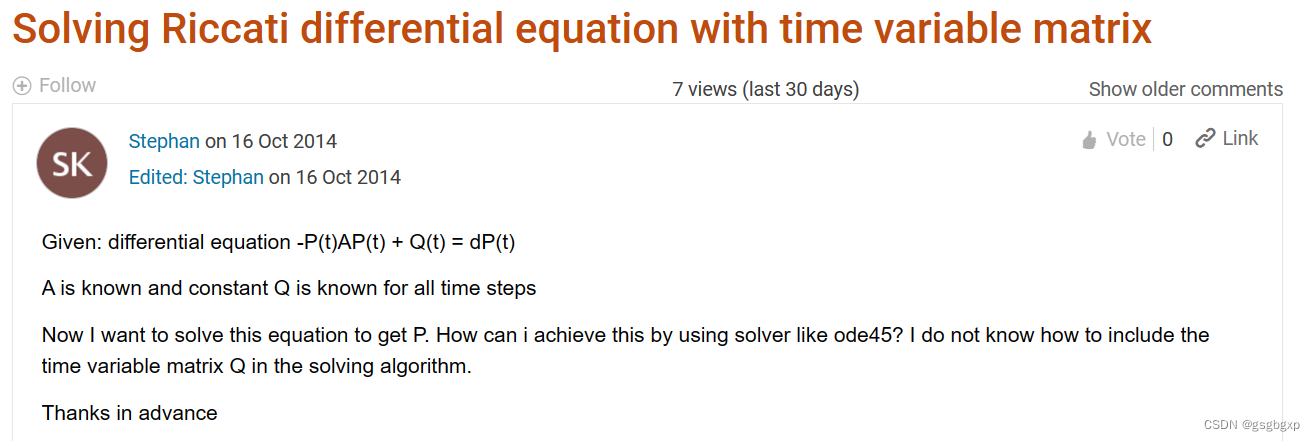
matlab的 ode45 函数官方文档的例子中有一个 ODE with Time-Dependent Terms。
内容如下

Consider the following ODE with time-dependent parameters
$$y^{\prime }(t)+f(t)y(t)=g(t).$$
The initial condition is $y_0=1$. The function f(t) is defined by the n-by-1 vector f evaluated at times ft. The function g(t) is defined by the m-by-1 vector g evaluated at times gt.

Create the vectors f and g.

ft = linspace(0,5,25);
f = ft.^2 - ft - 3;

gt = linspace(1,6,25);
g = 3*sin(gt-0.25);

Write a function named myode that interpolates f and g to obtain the value of the time-dependent terms at the specified time. Save the function in your current folder to run the rest of the example.
The myode function accepts extra input arguments to evaluate the ODE at each time step, but ode45 only uses the first two input arguments t and y.

function dydt = myode(t,y,ft,f,gt,g)
f = interp1(ft,f,t); % Interpolate the data set (ft,f) at time t
g = interp1(gt,g,t); % Interpolate the data set (gt,g) at time t
dydt = -f.*y + g; % Evaluate ODE at time t

Solve the equation over the time interval [1 5] using ode45. Specify the function using a function handle so that ode45 uses only the first two input arguments of myode. Also, loosen the error thresholds using odeset.

tspan = [1 5];
ic = 1;
opts = odeset('RelTol',1e-2,'AbsTol',1e-4);
[t,y] = ode45(@(t,y) myode(t,y,ft,f,gt,g), tspan, ic, opts);

Plot the solution, |y|, as a function of the time points, |t|.

plot(t,y)

三、如何处理“矩阵”微分方程

在上一节中给出的方法实际上是已经把矩阵微分方程变换成了一列，如果矩阵较大的话还是比较麻烦。
这个帖子给出了较好的解决方案 How can I solve the matrix Riccati differential equation within MATLAB?
或者还可参考
How can I solve a matrix differential equation within MATLAB?

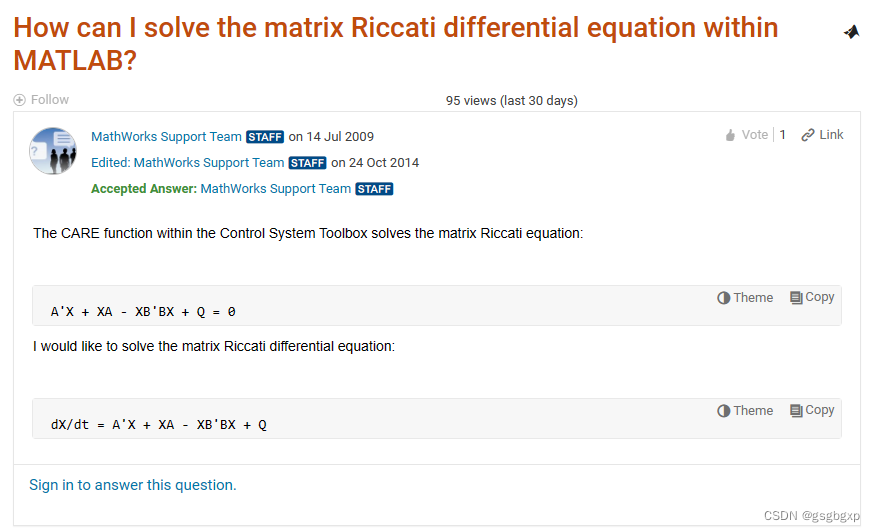
给出的解决方案如下
The matrix Riccati differential equation:

 dX/dt = A'X + XA - XBB'X + Q

can be solved using the functions in the ODE suite.
Assume your dependent matrix “X” is “n”-by-“n”, and you have known “n”-by-“n” matrices “A”, “B”, and “Q”. The following method will solve the matrix Riccati differential equation. Save the following as a MATLAB file somewhere on the MATLAB Path.

function dXdt = mRiccati(t, X, A, B, Q)
X = reshape(X, size(A)); %Convert from "n^2"-by-1 to "n"-by-"n"
dXdt = A.'*X + X*A - X*B*B.'*X + Q; %Determine derivative
dXdt = dXdt(:); %Convert from "n"-by-"n" to "n^2"-by-1

Then, you can use the ODE45 function to solve this problem:

[T X] = ode45(@(t,X)mRiccati(t, X, A, B, Q), [0 10], X0) 

For example, using the sample data:

A = [1 1; 2 1]; 
B = [1; 1]; 
Q = [2 1; 1 1];
X0 = [1; 1; 1; 1];

You can use the following command to solve the system of differential equation

[T X] = ode45(@(t,X)mRiccati(t, X, A, B, Q), [0 10], X0) 

ODE45 returns “X” as a vector at each time step. You may use the following code to reshape each row of “X” to get the matrix and store it in a cell array:

[m n] = size(X);
XX = mat2cell(X, ones(m,1), n);
fh_reshape = @(x)reshape(x,size(A));
XX = cellfun(fh_reshape,XX,'UniformOutput',false);

The results of this can be verified by the LQR function:

[K,S,E] = lqr(A, B, Q, 1)

where “S” should have results very similar to the last elements in “X” or “XX”. The LQR function computes the steady-state value of the system. In this example, we generated the solution for up to “t = 10”, which is an adequate approximation of infinity for this problem.

For more information on ODE45 and other such solvers, refer to the function reference page for ODE45 in the MATLAB documentation.

对于该方法网上还有人追问，如有需要可查阅

• https://www.mathworks.com/matlabcentral/answers/225984-how-can-i-solve-matrix-riccati-differential-equation
• how can i solve matrix riccati differential equation?

四、关于逆向积分

在上面的两个例子中给出的都是初始条件，但实际上Riccati方程给出的往往是终端条件，需要逆向(backward)积分。
对于简单的情况，微分方程中并不含自变量。
此时逆向积分并不复杂，只需要在定义时间区间tspan时把初始时刻和终端时刻调换即可，参考链接为
https://www.mathworks.com/matlabcentral/answers/151336-solving-differential-riccati-equation-with-a-boundary-condition

示例如下

par = [1;2;1];  % q0, q1, and q2
yf = 1;
ti = 0; tf = 2;
opt = odeset('AbsTol',1.0e-07,'RelTol',1.0e-07);
[t,y] = ode45( @riccatiEquation, [tf,ti], yf ,opt, par);

% Visualize
plot(t,y)

function dydx = riccatiEquation(x,y,parameters)
q0 = parameters(1);
q1 = parameters(2);
q2 = parameters(3);

dydx = q0 + q1*y + q2*y*y;
end

或者采用平移的方式，可参考吴受章的最优控制书。
如果实在不行，用变量代换转换成初值问题是不是也行？没有进行仿真验证。

其实对于这类问题有一个更广义的形式，即微分方程的多点边值问题，对此该类问题不能使用ode45解决，而应采用 BVP4C 或 BVP5C 来解决。参考链接如下

• Using ode45 to solve system of ODEs with some initial conditions and some terminal conditions
• Solve BVP with Multiple Boundary Conditions
• https://stackoverflow.com/questions/29162100/how-can-i-solve-a-system-of-odes-with-some-terminal-conditions-in-matlab

五、线性时变系统的Riccati矩阵微分方程

前段时间因事中断了一段时间，现在自己已经不面临这个问题了…
按照前几节的步骤似乎能解决这一问题，但没有经过仿真验证自己心里也不是很有底。

六、补充各类参考链接

时间有限，本来还想给几个例子，看之后自己还有没有机会吧。这里把一些自己在这个过程中的参考链接放上来

How can I solve riccati equation in Simulink with varying state space?

有一些链接给了代码，没来得及细看，但感觉似乎都是时不变系统的

• 这个代码声称解决的是时变矩阵微分方程，但得到的是近似解。而且还有论文支撑，看上去最靠谱 Recursive Approximate Solution to Matrix Diff. Riccati Eq.
• Solve Riccati Differential Equation (solve_riccati_ode)
• symmetric differential matrix Riccati equations
• 这份代码和上一份是同一个人上传到MathWorks网站上的，相差仅一天，可能是一样的 The solve the matrix Riccati differential equation
• Algebraic Riccati Equation Solver
• 这份代码也有论文，但似乎很专业，可能是数学专业的 Invariant Galerkin Ansatz Spaces and Davison-Maki Methods for the Numerical Solution of Differential Riccati Equations