声明:下面的方法不一定正确,个人学习过程中所写,并未做大量测试,仅供参考,应该有BUG,暂时不改了。
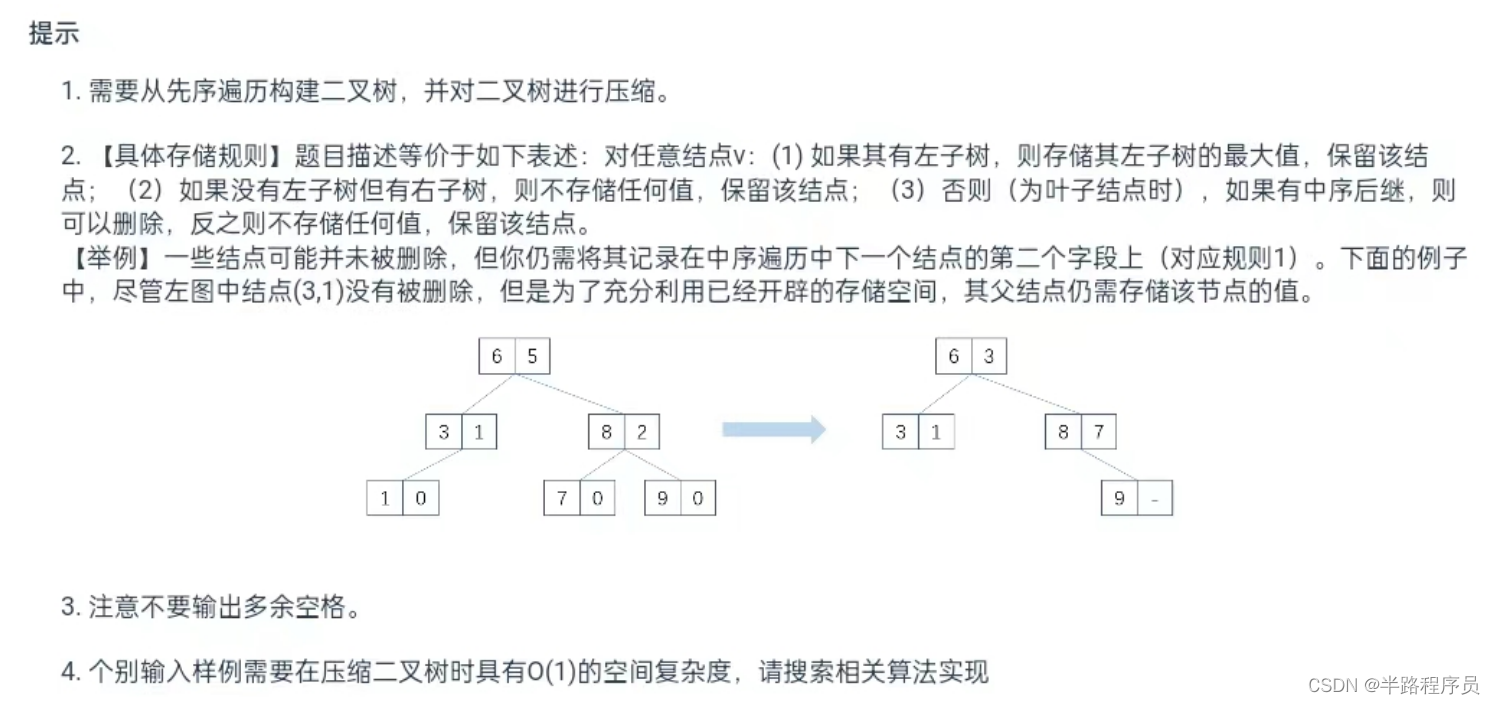
描述:某数据库为提升搜索效率,对某一整型字段构建二叉搜索树(BST)。每个结点包含两个数据信息: 1)结点的数据,2) 该结点子树的元素数目。为了压缩搜索树规模,该数据库为每个结点增加一个字段,该字段用于存储中序遍历时在访问该结点之前访问的结点数据。在该改进下,被存储的结点如果为叶子结点,该结点在新树中将被删除,以提高存储效率。如果一个叶子结点无中序后继,则无需删除。
给定该BST的先序遍历(第二个字段未给出),请编写程序,输出经过压缩后新BST的先序遍历结果。
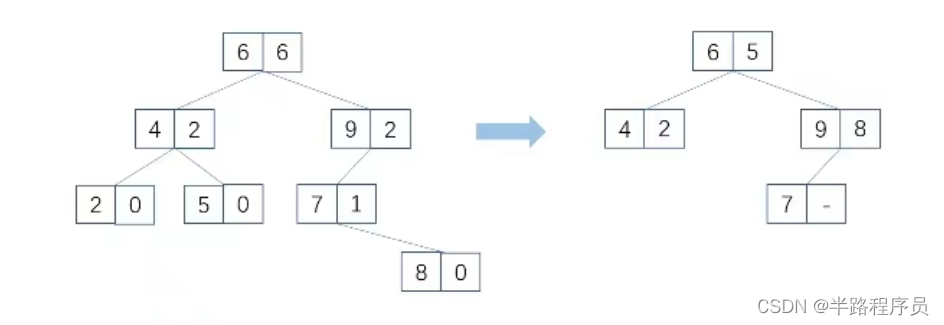
输入格式
输入共两行:第一行为一个int数据n,表示该BST的总结点个数。1<=n<=100000:第二行为n个int数据,为该BST的先序遍历结果(保证顺序是正确的,并保证数据两两不同)。 每个数据的范围:0<=X<=1*10^7。
输出格式
输出共一行:第一行为新BST的先序遍历结果,依序输出结点数据以及保存的其他结点数据(若没有则输出字符-)

#include <iostream>
#include <vector>
#include <map>
#include <stack>
using namespace std;
struct Node
{
int val, childNodes = 0;
Node* left, *right;
int left_type = 0;//类型标志
int right_type = 0;//类型标志
Node(int val, int childNodes):val(val),childNodes(childNodes),left(nullptr), right(nullptr) {}
};
// 根据先序遍历,创建一个二叉搜索树
Node* createBstFromPreOrder(vector<int>& preOrderNums, int left, int right) {
if (left > right) {
return nullptr;
}
Node* root = new Node(preOrderNums[left], right - left);
// 如果没有找到,mid为最右边值大1,这样左边的右边界为mid-1刚好就是数组最右边
int mid = right+1;
for (int i = left + 1; i <= right; i++) {
if (preOrderNums[i] > preOrderNums[left]) {
mid = i;
break;
}
}
root->left = createBstFromPreOrder(preOrderNums, left+1, mid-1);
root->right = createBstFromPreOrder(preOrderNums, mid, right);
return root;
}
// 线索化时的前一个结点
Node* pre = nullptr;
map<int, int> mp_delete;
//中序对二叉树进行线索化
void InThreading(Node* p){
//如果当前结点存在
if (p) {
InThreading(p->left);//递归当前结点的左子树,进行线索化
//如果当前结点没有左孩子,左标志位设为1,左指针域指向上一结点 pre
if (!p->left) {
p->left_type = 1;
p->left=pre;
}
//如果 pre 没有右孩子,右标志位设为 1,右指针域指向当前结点。
if (pre&&!pre->right) {
pre->right=p;
pre->right_type = 1;
p->childNodes = pre->val;
// 表示需要删除的节点
cout << "需要删除的节点:" << pre->val << endl;
mp_delete[pre->val] = 1;
}
pre=p;//pre指向当前结点
InThreading(p->right);//递归右子树进行线索化
}
}
void preorderBst(Node *root)
{
if(root != NULL)
{
Node *p = root;
while (p != NULL)
{
while (p->left_type == 0) // 左指针不是线索,则边访问边左移
{
cout << p->val << " " << p->childNodes << endl; // 访问结点
p = p->left; // 左移,访问左子树
}
cout << p->val << " " << p->childNodes << endl; // 此时p左必为线索,但还没有被访问,则访问
p = p->right; // 此时p左孩子不存在,则右指针若非空,则不论是否为线索都指向其后继
}
}
}
Node *Next(Node *t) //已知节点t找t的"后继"结点位置
{
if(t->right_type==1) //右标志为1,可以直接得到"后继"结点
{
t=t->right;
}
else /*右标志为0,不能直接的到"后继"结点,
则需要找到右子树最左下角的节点*/
{
t=t->right;
while(t->left_type==0)
{
t=t->left;
} //while
}//else
return t;
}
// 改方法用来遍历线索二叉树,当删除相关节点之后,线索被取消了,这个方法不能用
void InorderTraverse(Node *temp)//利用线索实现中序遍历
{
if(!temp)
{
return;
}
while(temp->left_type==0)//查找第一个节点
{ //因为二叉树的创建creat是以先序遍历序列创建,所以t所指向的第一个结点并不是中序遍历所要访问的第一个结点
temp=temp->left;
}
cout << "val:" << temp->val << " left_type:" << temp->left_type
<< " right_type:" << temp->right_type << " childNodes:" << temp->childNodes << endl;
while(temp->right)// 此处以"t的右孩子不为空"为循环条件,是因为,先前设定了最后一个结点的"后继"为空,表示结束
{ //根据线索访问后续结点
temp=Next(temp);
cout << "val:" << temp->val << " left_type:" << temp->left_type
<< " right_type:" << temp->right_type << " childNodes:" << temp->childNodes << endl;
}
}
// 用mp记录第一次出现时,用来向左走时判断,如果之前出现过,则不向走了,表是左边已经走过了
map<int, int> mp;
// 删除相关节点,将线索取消掉
void deleteBstNode(Node* root) {
if (root == nullptr) return;
stack<Node*> stk;
Node* p = root;
while (p != nullptr || stk.size()) {
// 当没有出现过,且左边有孩子
while(p->left && p->left->left_type == 0 && mp[p->val] == 0) {
stk.push(p);
mp[p->val] = 1;
p = p->left;
}
// 如果左边的孩子拥有前驱结点,则取消前驱标志
if (p->left && p->left->left_type == 1 && p->left->left && mp[p->val] == 0) {
stk.push(p);
mp[p->val] = 1;
// 将其中序的前一个结点置为-1,标志为“-”
p->childNodes = -1;
p = p->left;
p->left = nullptr;
p->left_type = 0;
}
// 表示左边需要删除
else if (p->left && mp[p->val] == 0) {
cout << "删除了---" << p->left->val << endl; //2
p->left->right = nullptr;
p->left = nullptr;
}
// 如果右边没有了,或者刚好右边有一个需要删除
if((p->right == nullptr && stk.size()) || (p->right && p->right->right_type == 1)) {
while ((p->right == nullptr && stk.size()) || (p->right && p->right->right_type == 1)) {
// 右边需要删除
if (p->right && p->right->right_type == 1) {
cout << "删除了+++" << p->right->val << endl; // 5
p->right->right = nullptr;
p->right = nullptr;
} else if(p->right){
// 不需要删除
p = p->right;
break;
}
p = stk.top();
stk.pop();
}
// 不满足上述条件时,将p右移动
if (p->right && p->right->right_type == 0) {
p = p->right;
}
} else if (p->right && p->right->right_type == 0) {
p = p->right;
} else {
// 最后不满足时一定要返回
return;
}
}
}
// 二叉树递归先序遍历
void preOrder(Node* root) {
if (root == nullptr) {
return;
}
cout << root->val << " " << root->childNodes << " " << endl;;
preOrder(root->left);
preOrder(root->right);
}
// 二叉树递归中序遍历
void inOrder(Node* root) {
if (root == nullptr) {
return;
}
inOrder(root->left);
cout << root->val << " " << root->childNodes << " " << endl;;
inOrder(root->right);
}
// 二叉树递归后续遍历
void postOrder(Node* root) {
if (root == nullptr) {
return;
}
postOrder(root->left);
postOrder(root->right);
cout << root->val << " " << root->childNodes << " " << endl;;
}
// 下面这个访问线索二叉树方法有问题
// void inOrderTraverse(Node* root)
// {
// //从根节点开始先找到最左边
// if (root == NULL)
// {
// return;
// }
// Node* temp = root;
// //先找到最左边结点 然后根据线索化直接向右遍历
// while (temp != NULL && temp->left_type == 0)
// {
// temp = temp->left;
// }
// while (temp != NULL)
// {
// //输出
// cout << "val:" << temp->val << " left_type:" << temp->left_type
// << " right_type:" << temp->right_type << " childNodes:" << temp->childNodes << endl;
// temp = temp->right;
// }
// }
int main() {
vector<int> nums = {6, 4, 2, 5, 9, 7, 8};
Node * head = createBstFromPreOrder(nums, 0, nums.size()-1);
preOrder(head);
cout << "=====================================" << endl;
inOrder(head);
cout << "=====================================" << endl;
postOrder(head);
cout << "=====================================" << endl;
// 线索化二叉树
InThreading(head);
// 删除相关节点
deleteBstNode(head);
// 遍历二叉树
preOrder(head);
cout << "=====================================" << endl;
cin.get();
return 0;
}
![[ 云计算 | AWS 实践 ] 使用 Java 列出存储桶中的所有 AWS S3 对象](https://img-blog.csdnimg.cn/a82e8ccbf79d485299e41259558d41a5.png)