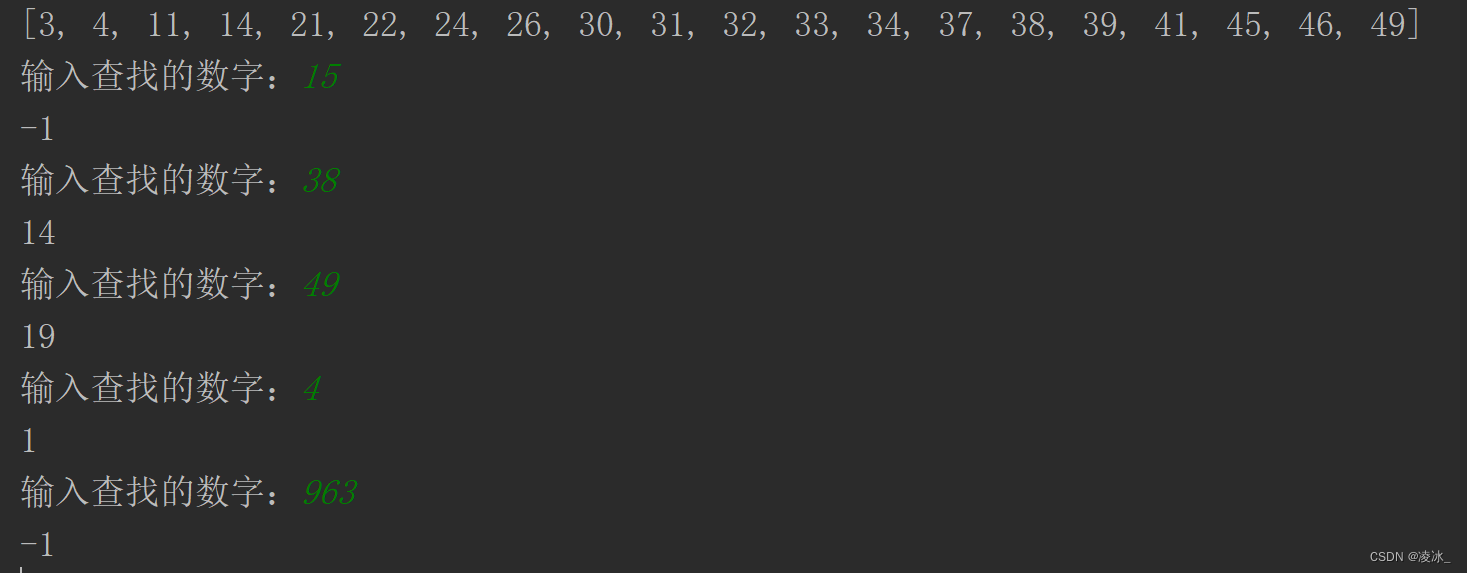
trie树
#include <iostream>
using namespace std;
const int N = 1000010;
int son[N][26],cnt[N],idx;
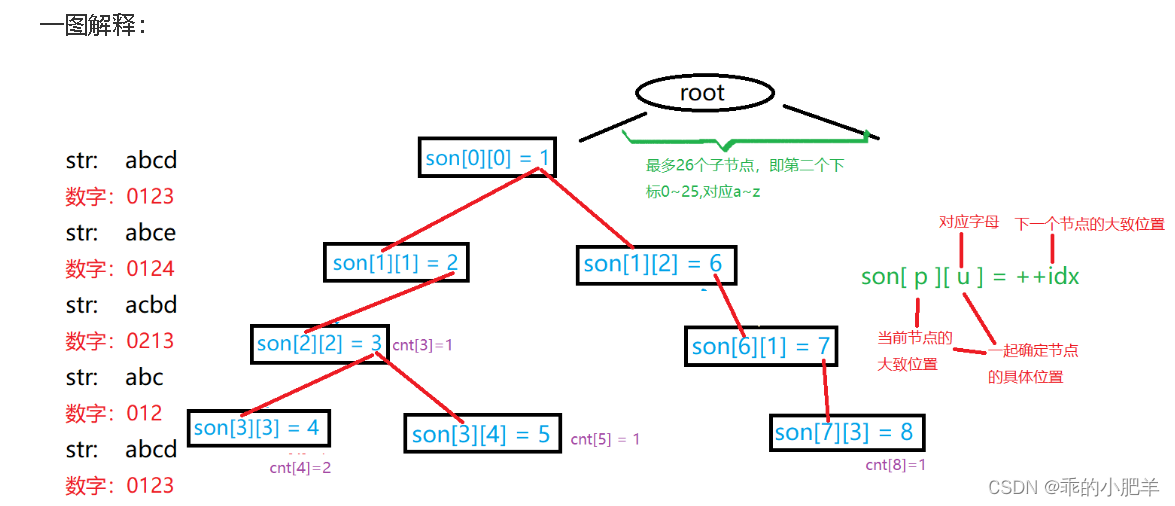
//明确前面两个数组以及idx的含义
//我们把son这个二维数组看成一个字典树
//本题要求26个字母,所以我们每个节点里面最多有26个儿子节点
//而我们本题要求字符串长度是100000个,所以son数组的N代表有100000层,对应的就是字符串长度
//为什么这样就可以呢,因为我们查找的字符串(只有26个字母)在查找的时候想象成树
//每次面临26种选择(26个字母)(也有点组合的意思),选择一种和当前匹配的,没有就说明没有匹配的
//idx是什么呢,我们怎么用数组来模拟的呢,我们怎么算是创建过这个节点了,我们son数组的元素为1
//就代表我们创建了这个节点,如果遇到这个节点之后我们就可以直接往下走,如果没有遇到,我们就
//不往下走,先创建在走,创建的过程就是idx++,就是走到当前元素为1时说明创建过了
//cnt数组表示以当前节点的值为终点的字符串个数
char str[N];
void insert(char str[])
{
int p = 0;//p代表我们当前走到哪个位置了(把数组抽象成一棵树)
for(int i = 0; str[i] != '\0';i++)//枚举插入的字符串,枚举的字符串抽象成路径
{
int u = str[i] - 'a';//映射到数组里,son数组一维数组的下标0代表的是a,1是b
if(son[p][u] == 0) son[p][u] = ++idx;//每次进入判断是否创建过当前值的节点
p = son[p][u];//走到下一层
}
cnt[p]++;//当前下标为终点的字符串个数++
}
int inquire(char str[])
{
int p = 0;
for(int i = 0; str[i] != '\0';i++)
{
int u = str[i] - 'a';
if(!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
int main()
{
int n;
cin>>n;
for(int i = 0;i < n;i++)
{
char chose[2];
cin>>chose>>str;
if(chose[0] == 'I')
{
insert(str);
}
else
{
printf("%d\n",inquire(str));
}
}
return 0;
}并查集
#include <iostream>
#include <algorithm>
#include <vector>
#include <cstring>
using namespace std;
//本题是模板题,所以我们先理解这道题的模板是什么
//本题的模板是并查集,那什么是并查集呢,其实你可以想象成一个树
//我们的字符串都是通过递归去搜索的,跟字典树类似
//但是并查集强在归并和询问的操作近乎O(1)的时间复杂度,可以快速将两个集合
//合并和快速查两个集合是否在同一个集合
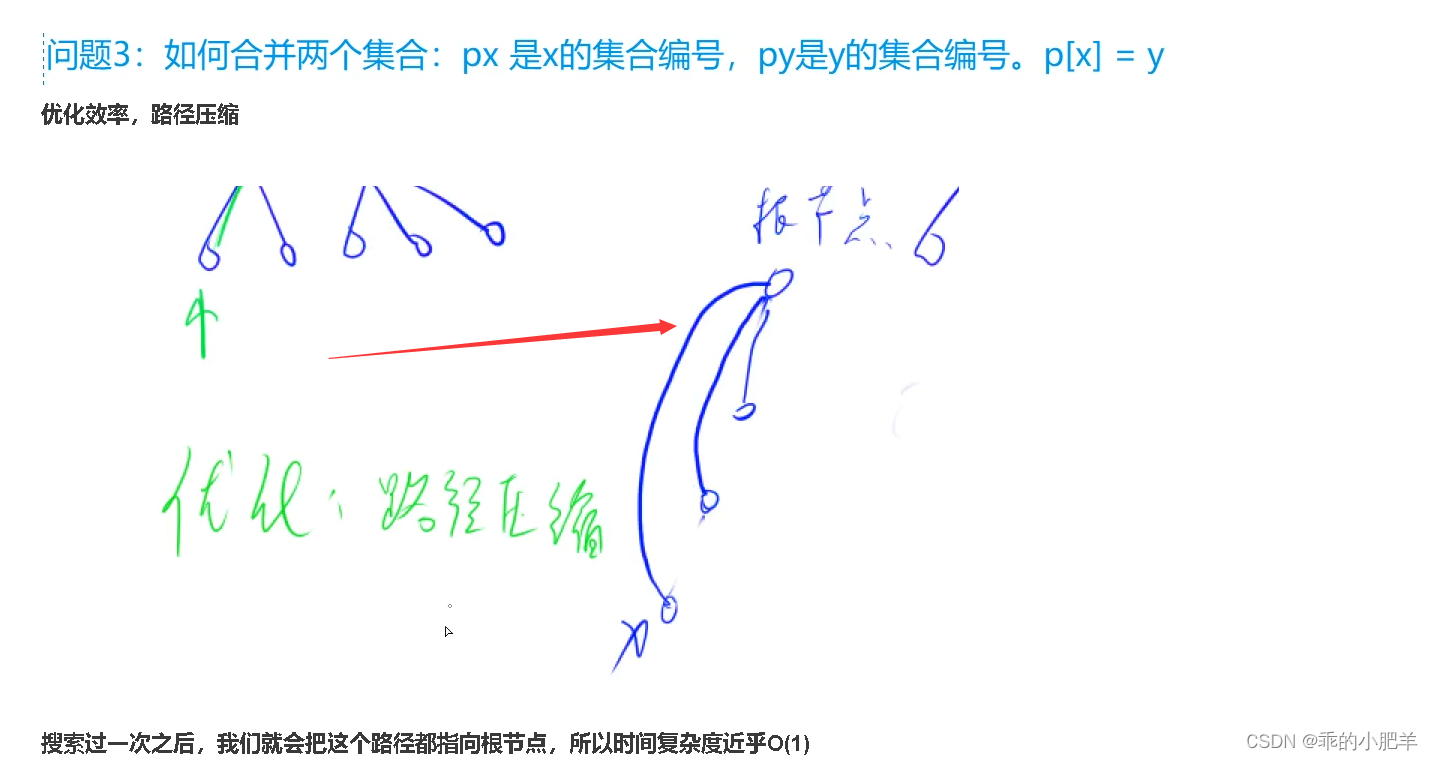
//并查集的基本原理是什么呢,基本原理就是每个集合我们看成一颗小树,一颗大树里可能包含小树
//比方说一个字符串是一个集合,那么这棵大树可能就有好多字符串集合,
//那我们并查集是怎么快速实现合并和查询的呢,这就要说到并查集的编号了
//我们怎么去查找到这个集合呢,我们肯定得让他的根节点跟孩子节点编号不一样,我们才能找到
//我们的集合,在此我们设置P[x]为节点的编号,而p[x] == x 是根节点的编号
//我们的p[x]代表的是当前节点的父节点
//1.如何判断根节点 if(p[x] == x)
//2.如何从孩子节点求根节点的编号while(p[x]!=x) x = p[x];
//3.如何合并两个集合,假设编号是p[X],P[Y],前面提到过的我们抽象成一颗树,这棵树
//合并只需要把一个根节点作为另一个根节点的父节点即可
//在此,我们还需要优化一下,路径压缩法,等于说第一次查询过这个集合之后下次查询就是O(1)的
//时间复杂度,为什么呢,想象一下一棵树的高度只有2,根节点只有1个,这时我们查询集合的所以元素的话
//我们就只需要遍历这个集合就元素就行,不需要再去递归好几层了
//并查集模板最关键的点是在于写出find操作
const int N = 1000010;
int p[N];
int find(int x)//返回要查找的元素的集合,递归查找
{
if(p[x] != x) p[x] = find(p[x]);//如果父节点不是根节点,那么就把接力棒给父节点
//让父亲节点去找
return p[x];//找到了就返回
}
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1;i <= n;i++) p[i] = i;
while (m--)
{
char op[2];
int a, b;
scanf("%s%d%d",op,&a,&b);
if (op[0] == 'Q')
{
if (find(a) == find(b)) printf("Yes\n");
else printf("No\n");
}
else if(op[0] == 'M')
{
p[find(a)] = find(b);//找到a集合的根节点,把a集合的根节点查到b集合的根节点
}
}
return 0;
}
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510000;
int p[N],d[N];
int n,m;
int find(int x)//路径压缩
{
if(p[x] != x)//不是根节点的话
{
int t = find(p[x]);
d[x] += d[p[x]];
p[x] = t;
}
return p[x];
}
int main()
{
cin>>n>>m;
for(int i = 1;i <= N;i++)
{
p[i] = i;
}
int cnt = 0;
for(int i = 1;i <= m;i++)
{
int op,a,b;
cin>>op>>a>>b;
if(a > n || b > n)
{
cnt++;
continue;
}
int pa = find(a);
int pb = find(b);
if(op == 1)
{
if(pa == pb && (d[a] - d[b]) % 3){
//是在同一个集合的话,判断是否是同类
//不是同类res++,是同类不用管
cnt++;
}
else if(pa != pb){
//不在同一个集合,判断是否同类
//先建立两个集合的集合关系,为什么建立两个呢
//因为能find找到说明必有根节点
//本题根节点肯定存在,就算只有两个节点
//我们也看成两个集合
p[p[a]] = pb;//让x集合的根节点作为y集合的根节点的孩子
//节点
//建立之后还得更新一下距离关系,第一次进入的话其实
//并没有建立集合,也就是刚好是说了第一句话的时候
//第一句不同的x和y或者两个相同的x或者y我们默认为真话,
//默认为x和y同类并且建立关系(同类关系)
//所以x和y分别到当前建立好集合关系
//的根节点的距离一定要相等,所以距离
//就是d[x] + ?= d[y],这个问好是根节点到px的距离
d[pa] = d[b] - d[a];
}
}
else
{
if(pa == pb && (d[a] - d[b] -1) %3){
//在同一个集合
//并且不是x 吃 y的关系
//c++中-n % n等于0
cnt++;
}
else if(pa != pb){
//不是同一个集合的话,那么我们默认为
//真话,x能吃掉y
p[p[a]] = pb;
//维护距离使得x能吃掉y
d[pa] = d[b] - d[a] + 1;
}
}
}
cout<<cnt<<endl;
return 0;
}