探讨jdk源码中的二分查找算法返回值巧妙之处

文章目录

1.什么是二分查找算法
- 1.1 简介
- 1.2 实现思路
2.二分查找的示例
3.jdk 中的 Arrays.binarySearch()
4.jdk 中核心二分查找方法解析
- 4.1 为什么 low 是插入点
- 4.2 为什么要进行取反：-（low + 1）
- 4.3 为什么不直接返回插入点 low 的相反数，还需要进行 +1 操作
- 4.4 可以将 +1 改为 -1 吗
5.未找到目标元素时根据返回值进行数组扩容

1.什么是二分查找算法

1.1 简介

二分查找算法，也称 折半查找 算法，是一种在 有序数组 中查找某一特定元素的搜索算法。

1.2 实现思路

初始状态下，将整个序列作为搜索区域。
找到搜索区域内的中间元素，和目标元素进行比对。
- 如果相等，则搜索成功；
- 如果中间元素大于目标元素，表明目标元素位于中间元素的左侧，将左侧区域作为新的搜素区域；
- 反之，若中间元素小于目标元素，表明目标元素位于中间元素的右侧，将右侧区域作为新的搜素区域；
重复执行第二步，直至找到目标元素。如果搜索区域无法再缩小，且区域内不包含任何元素，则表明整个序列中没有目标元素，查找失败。

2.二分查找的示例

/**
 * 二分查找（升序数组版）
 *
 * @param array       待查找的升序数组
 * @param targetValue 待查找的目标值
 * @return 找到则返回目标值的索引，找不到返回-1
 */
public static int binarySearch(int[] array, int targetValue) {
    // 左边界
    int left = 0;
    // 右边界
    int right = array.length - 1;

    int mid;

    while (left <= right) {
        /*
            考虑到 left+right 的值可能会超过 int可表示 的最大值，我们不再对他们的和直接除以2
            我们知道 除以2 的操作可以用 位运算 >>1 来代替
            但还不够，由于 (left+right) 值溢出表示负数，>>1 只是做 除以2 操作，最高位符号位不变，依旧为1表示负数，负数除以2依旧是负数
            这时候我们可以修改为 无符号右移 >>>1 ，低位溢出，高位补0，那么最高位符号位为0就表示正数了
         */
        mid = (left + right) >>> 1;

        if (targetValue < array[mid]) {
            // 如果查找的目标值比中间索引值小，则缩小查找的右边界
            right = mid - 1;
        } else if (array[mid] < targetValue) {
            // 如果中间索引值小于查找的目标值，则缩小查找的左边界
            left = mid + 1;
        } else {
            // 如果找到了，就返回目标索引
            return mid;
        }
    }

    // 退出了 while 循环，说明如果没找到，则返回 -1 表示未找到
    return -1;
}

3.jdk 中的 Arrays.binarySearch()

public class Arrays {
    public static int binarySearch(int[] a, int key) {
        return binarySearch0(a, 0, a.length, key);
    }

    private static int binarySearch0(int[] a, int fromIndex, int toIndex,
                                     int key) {
        int low = fromIndex;
        int high = toIndex - 1;

        while (low <= high) {
            int mid = (low + high) >>> 1;
            int midVal = a[mid];

            if (midVal < key)
                low = mid + 1;
            else if (midVal > key)
                high = mid - 1;
            else
                return mid; // key found
        }
        return -(low + 1);  // key not found.
    }
}

有了刚才二分查找的示例，其实 jdk 中二分查找方法的实现也几乎差不多，只是返回值与我们的示例不同。当目标值在数组中找不到时：

我们的示例会返回 -1 作为找不到元素的标识；
而 jdk 中是将 目标值的待插入点的变式 作为找不到元素的标识。这意味着我们可以对这个返回值做更多的事情，例如当目标值不存在时根据待插入点进行数组扩容，将目标值加入到数组中。

关于 jdk 中找不到目标值情况的返回值，我们举个例子来帮助更好理解什么是 目标值的待插入点的变式：

已知数组 [2, 5, 8]，待查找的目标值是 4；
很明显，在数组中并不存在 4，那么 jdk 中的二分查找算法返回值是 -2，那么根据 返回值 = -(插入点 + 1) 可以推导出插入点应该是 1，也就是数组索引为 1 的位置；
即，如果需要将未找到的目标值 4 插入到数组中，应该放在索引为 1 的位置，即索引为 0 的元素 2 的后面。

索引 0 1 2 3
原数组 2 5 8
新数组 2 4 5 8

索引	0	1	2	3
原数组	2	5	8
新数组	2	4	5	8

4.jdk 中核心二分查找方法解析

/**
 * 使用二分搜索算法在指定的整数数组中搜索指定的值。在进行此调用之前，必须对数组进行排序（按方法排序 sort(int[]) ）。
 * 如果未排序，则结果未定义。如果数组包含多个具有指定值的元素，则无法保证会找到哪个元素。
 * 参数：
 * a – 要搜索的数组
 * key – 要搜索的值
 * 返回：搜索键的索引（如果它包含在数组中）;否则返回 -（插入点 + 1）。
 * 插入点定义为将键插入数组的 点 ：第一个元素的索引大于键，如果数组中的所有元素都小于指定的键，则为 a.length 。
 * 请注意，这保证了当且仅当找到键时返回值将为 >= 0。
 */
public static int binarySearch(int[] a, int key) {
    return binarySearch0(a, 0, a.length, key);
}

// Like public version, but without range checks.
private static int binarySearch0(int[] a, int fromIndex, int toIndex,
                                 int key) {
    // 左边界
    int low = fromIndex;
    // 右边界
    int high = toIndex - 1;

    while (low <= high) {
        int mid = (low + high) >>> 1;
        int midVal = a[mid];

        if (midVal < key)
            low = mid + 1;
        else if (midVal > key)
            high = mid - 1;
        else
            return mid; // key found
    }

    // 返回 -(插入点 + 1)
    return -(low + 1);  // key not found.
}

我们现在需要思考两个问题：

为什么 low 是插入点
为什么要进行取反：-（low + 1）
为什么不直接返回插入点 low 的相反数，还需要进行 +1 操作
可以将 +1 改为 -1 吗

4.1 为什么 low 是插入点

以已知了找不到目标结果为前提，有这样几件事我们需要明白：

随着循环次数增加，low 与 high 的距离会越来越近。直到刚进入最后一轮循环时，一定是 low == high。
最终未查找目标时，退出了 while 循环，会有 low > high，且 low = high + 1

// 最后一轮进入循环时，low == high
while (low <= high) {
    
    // 那么 mid == high == low
    int mid = (low + high) >>> 1;
    
    int midVal = a[mid];

    /*
    	要么进入 if，要么进入 else if
    		1.当中间值小于目标值时，意味着待插入的目标值应该要在中间值索引 mid 后面一个位置，
    		  即就是 low = mid + 1，所以 low 就是插入点
    		  
            2.当目标值小于中间值时，意味着待插入的目标值应该要在中间值索引 mid 前面一个位置，
              既然要排到 mid 的前面一个位置，不就意味着要将 mid 位置挤占，将 mid 及之后的元素向后移动一位吗？
              所以插入点也就是当前 mid 的位置，而 low 是等于 mid 的，所以等价于 low 就是插入点 
    */
    
    if (midVal < key)
        low = mid + 1;
    else if (midVal > key)
        high = mid - 1;
    else
        return mid; // key found
}

4.2 为什么要进行取反：-（low + 1）

我们用正数来标识在数组中找到的目标值的索引。

因为 low + 1 一定是正数，。因此只能取反得到负数标识未找到目标值，再反推变式得到插入点。

4.3 为什么不直接返回插入点 low 的相反数，还需要进行 +1 操作

📑 例如对于数组 [2, 5, 8]，我们需要查找目标值为 -6 的索引，那么肯定是找不到的，循环结束时得到的 low 是 0，也就是目标值需要插在索引为 0 的位置。

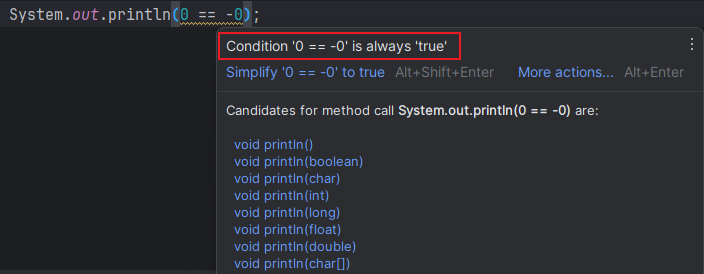
如果返回的不是 -(low + 1) 而是 -low，即 -0。在 Java 中，0 == -0 为 true，因此会被认为是索引为 0 的位置找到了目标值。

4.4 可以将 +1 改为 -1 吗

不可以，low + 1 的结果一定是正数，但 low - 1 的结果能保证一定是正数吗？是不能的，比如当待插入点 low 为 1 时，最终返回结果 -(low - 1) 的结果为 0。那么会被认为目标值找到了且索引为 0，这是不合理的。

5.未找到目标元素时根据返回值进行数组扩容

public static void main(String[] args) {
    // 二分查找目标值，不存在则插入
    /*
        原始数组：[2,5,8]
        查找目标值：4
        查询不到，返回的结果为 r = -待插入点索引-1
        在这里带插入点索引为 1，对应 r = -2
        那么我们分成这几步来进行拷贝：
            - 1.新建数组,大小为原数组的大小+1：         [0,0,0,0]
            - 2.将待插入点索引之前的数据放入新数组：     [2,0,0,0]
            - 3.将目标值放入到待插入点索引的位置：       [2,4,0,0]
            - 4.将原数组后面的数据都相继拷贝到新数组后面： [2,4,5,8]
     */

    // 定义原数组与目标值
    int[] oldArray = {2, 5, 8};
    int target = 4;

    // 搜索目标值4，没有找到，返回结果为 r =  -待插入点索引-1，这里的 r=-2
    int r = Arrays.binarySearch(oldArray, target);

    // r < 0 说明没有找到目标值，就插入
    if (r < 0) {
        // r = -(插入点 + 1) => 插入点 = -r - 1
        // 获取待插入索引
        int insertIndex = -r - 1;

        // 1.新建数组,大小为原数组的大小+1
        int[] newArray = new int[oldArray.length + 1];

        // 2.将待插入点索引之前的数据放入新数组
        // 新数组由 [0,0,0,0] --> [2,0,0,0]
        for (int i = 0; i <= insertIndex - 1; i++) {
            newArray[i] = oldArray[i];
        }

        // 3.将目标值放入到待插入点索引的位置
        // 新数组由 [2,0,0,0] --> [2,4,0,0]
        newArray[insertIndex] = target;

        // 4.将原数组后面的数据都相继拷贝到新数组后面
        // 新数组由 [2,4,0,0] --> [2,4,5,8]
        for (int i = insertIndex; i <= oldArray.length - 1; i++) {
            newArray[i + 1] = oldArray[i];
        }

        System.out.println(Arrays.toString(newArray)); // [2, 4, 5, 8]
    }

}

当然，第二步和第四步拷贝的方法其实类似，我们可以自己封装一个公共方法 myArraycopy 来进行调用：

public static void main(String[] args) {
    // 二分查找目标值，不存在则插入
    /*
        原始数组：[2,5,8]
        查找目标值：4
        查询不到，返回的结果为 r = -待插入点索引-1
        在这里带插入点索引为 1，对应 r = -2
        那么我们分成这几步来进行拷贝：
            - 1.新建数组,大小为原数组的大小+1：         [0,0,0,0]
            - 2.将待插入点索引之前的数据放入新数组：     [2,0,0,0]
            - 3.将目标值放入到待插入点索引的位置：       [2,4,0,0]
            - 4.将原数组后面的数据都相继拷贝到新数组后面： [2,4,5,8]
     */

    // 定义原数组与目标值
    int[] oldArray = {2, 5, 8};
    int target = 4;

    // 搜索目标值4，没有找到，返回结果为 r =  -待插入点索引-1，这里的 r=-2
    int r = Arrays.binarySearch(oldArray, target);

    // r < 0 说明没有找到目标值，就插入
    if (r < 0) {
        // r = -(插入点 + 1) => 插入点 = -r - 1
        // 获取待插入索引
        int insertIndex = -r - 1;

        // 1.新建数组,大小为原数组的大小+1
        int[] newArray = new int[oldArray.length + 1];

        // 2.将待插入点索引之前的数据放入新数组
        // 新数组由 [0,0,0,0] --> [2,0,0,0]
        myArraycopy(oldArray, 0, newArray, 0, insertIndex);

        // 3.将目标值放入到待插入点索引的位置
        // 新数组由 [2,0,0,0] --> [2,4,0,0]
        newArray[insertIndex] = target;

        // 4.将原数组后面的数据都相继拷贝到新数组后面
        // 新数组由 [2,4,0,0] --> [2,4,5,8]
        myArraycopy(oldArray, insertIndex, newArray, insertIndex + 1, oldArray.length - insertIndex);

        System.out.println(Arrays.toString(newArray));
    }

}

/**
 * 数组元素拷贝
 *
 * @param oldArray               旧数组
 * @param oldArrayStartCopyIndex 旧数组元素开始拷贝的位置
 * @param newArray               新数组
 * @param newArrayStartCopyIndex 新数组元素开始拷贝的位置
 * @param copyLength             拷贝的元素长度（个数）
 */
public static void myArraycopy(int[] oldArray,
                               int oldArrayStartCopyIndex,
                               int[] newArray,
                               int newArrayStartCopyIndex,
                               int copyLength) {
    for (int i = 0; i < copyLength; i++) {
        newArray[newArrayStartCopyIndex++] = oldArray[oldArrayStartCopyIndex++];
    }
}

但当然，其实 jdk 已经为我们提供了数组元素拷贝的方法 System.arraycopy，jdk 提供的这个方法的作用和我们自定义的 myArrayCopy 方法参数和效果是一样的，因此我们完全可以将拷贝方法修改为 System.arraycopy：

public static void main(String[] args) {
    // 二分查找目标值，不存在则插入
    /*
        原始数组：[2,5,8]
        查找目标值：4
        查询不到，返回的结果为 r = -待插入点索引-1
        在这里带插入点索引为 1，对应 r = -2
        那么我们分成这几步来进行拷贝：
            - 1.新建数组,大小为原数组的大小+1：         [0,0,0,0]
            - 2.将待插入点索引之前的数据放入新数组：     [2,0,0,0]
            - 3.将目标值放入到待插入点索引的位置：       [2,4,0,0]
            - 4.将原数组后面的数据都相继拷贝到新数组后面： [2,4,5,8]
     */

    // 定义原数组与目标值
    int[] oldArray = {2, 5, 8};
    int target = 4;

    // 搜索目标值4，没有找到，返回结果为 r =  -待插入点索引-1，这里的 r=-2
    int r = Arrays.binarySearch(oldArray, target);

    // r < 0 说明没有找到目标值，就插入
    if (r < 0) {
        // r = -(插入点 + 1) => 插入点 = -r - 1
        // 获取待插入索引
        int insertIndex = -r - 1;

        // 1.新建数组,大小为原数组的大小+1
        int[] newArray = new int[oldArray.length + 1];

        // 2.将待插入点索引之前的数据放入新数组
        // 新数组由 [0,0,0,0] --> [2,0,0,0]
        System.arraycopy(oldArray, 0, newArray, 0, insertIndex);

        // 3.将目标值放入到待插入点索引的位置
        // 新数组由 [2,0,0,0] --> [2,4,0,0]
        newArray[insertIndex] = target;

        // 4.将原数组后面的数据都相继拷贝到新数组后面
        // 新数组由 [2,4,0,0] --> [2,4,5,8]
        System.arraycopy(oldArray, insertIndex, newArray, insertIndex + 1, oldArray.length - insertIndex);

        System.out.println(Arrays.toString(newArray));
    }

}