1. 栈(Stack)

1.1 概念

栈 ：一种特殊的线性表，其 只允许在固定的一端进行插入和删除元素操作 。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO （ Last In First Out ）的原则。

压栈：栈的插入操作叫做进栈 / 压栈 / 入栈， 入数据在栈顶 。

出栈：栈的删除操作叫做出栈。 出数据在栈顶 。

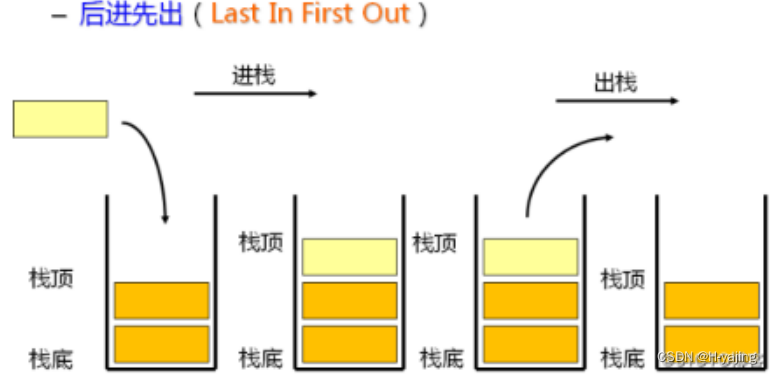
1.2 栈的使用 

方法	功能
Stack()	构造一个空的栈
E push(E e)	将e入栈，并返回e
E pop()	将栈顶元素出栈并返回
E peek()	获取栈顶元素
int size()	获取栈中有效元素个数
boolean empty()	检测栈是否为空

1.3 栈的模拟实现 

栈和ArrayList类似，都是动态的顺序表 ，我们用数组来实现。

首先，我们自己创建一个类MyStack，里面定义一个数组成员变量，用来模拟实现栈 ，代码：

public class MyStack implements IStack{
    private int[] elem;
    private int usedSize;  //数组中元素的个数
    private static final int DEFAULT_CAPACITY = 10;  //默认数组大小

    public MyStack() {
       elem = new int[DEFAULT_CAPACITY];
    }
}

对于栈的实现：入栈操作 

在入栈的时候，要先判断数组是否已满，如果满，则对数组进行扩容；不满，则直接在数组的最后加入元素。

    public void push(int x) {
        if (full()) {
            elem = Arrays.copyOf(elem,2*elem.length);
        }
        elem[usedSize]=x;
        usedSize++;
    }

    public boolean full() {
        if (usedSize == elem.length) {
            return true;
        }
        return false;
    }

对于栈的实现：出栈操作  

在出栈的时候，首先判断一下栈是否为空，为空的话抛出EmptyException异常，实现栈是否为空，代码：

    public boolean empty() {
        //栈为空，也就是数组里面没有元素
        return usedSize == 0;
    }

出栈操作： 

    public int pop() {
        if(empty()) {
            throw new EmptyException("栈为空！"); //自定义异常
        }
        int old = elem[usedSize-1];
        usedSize--;  //相当于删除
        return old;
    }

自定义异常：

public class EmptyException extends RuntimeException{
    public EmptyException(String msg) {
        super(msg);
    }
}

对栈的实现：peek()操作

peek()操作是查看栈顶元素的值，若栈为空，则抛出EmptyException异常；不空，直接返回数组最后一个元素的值即可。

    public int peek() {
        if(empty()) {
            throw new EmptyException("栈为空！");
        }
        return elem[usedSize-1];
    }

 对栈的实现：栈的大小

栈的大小，直接返回数组元素的个数即可。 

    public int size() {
        return usedSize;
    }

1.4 栈的应用场景 

1. 改变元素的序列  

1. 若进栈序列为 1,2,3,4 ，进栈过程中可以出栈，则下列不可能的一个出栈序列是（C）

     A: 1,4,3,2 B: 2,3,4,1 C: 3,1,4,2 D: 3,4,2,1

2. 一个栈的初始状态为空。现将元素 1 、 2 、 3 、 4 、 5 、 A 、 B 、 C 、 D 、 E 依次入栈，然后再依次出栈，则元素出栈的顺序是（B ）。

    A: 12345ABCDE B: EDCBA54321 C: ABCDE12345 D: 54321EDCBA

2. 将递归转化为循环  

比如：逆序打印链表 

// 递归方式
void printList(Node head){
    if(null != head){
        printList(head.next);
        System.out.print(head.val + " ");
    }
}
// 循环方式
void printList(Node head){
    if(null == head){
        return;
    }
    Stack<Node> s = new Stack<>();
    // 将链表中的结点保存在栈中
    Node cur = head;
    while(null != cur){
        s.push(cur);
        cur = cur.next;
    }
    // 将栈中的元素出栈
    while(!s.empty()){
        System.out.print(s.pop().val + " ");
    }
}