学习目的

SPSS第九讲 | 两因素析因设计的方差分析，超级详细

软件版本

IBM SPSS Statistics 26。

原始文档

《小白爱上SPSS》课程
#统计原理

两因素析因设计的方差分析

析因设计，也称全因子实验设计，是一种将两个或多个因素的各水平交叉分组，对各个组合都进行实验的设计。它可以分析各实验因素的主效应、各因素间的交互效应和简单效应。
主效应（main effect）：指某一因素各单独效应的平均效应，即某一因素各水平之间的平均差别。
交互效应（interaction effect )：指某一因素的单独效应随着另一因素的水平变化而变化。
简单效应（simple effect）：指固定其中一个因素某一个水平时，探讨另一个因素不同水平的效应之差。当两个因素间存在交互效应，须逐一分析各因素的简单效应。

一、实战案例

针对大侠们的肥胖问题，小白制定了不同干预方案。
干预方案1为运动训练，分为低强度、中强度和高强度3个水平；
干预方案2为饮食控制，分为一般控制和严格控制2个水平。
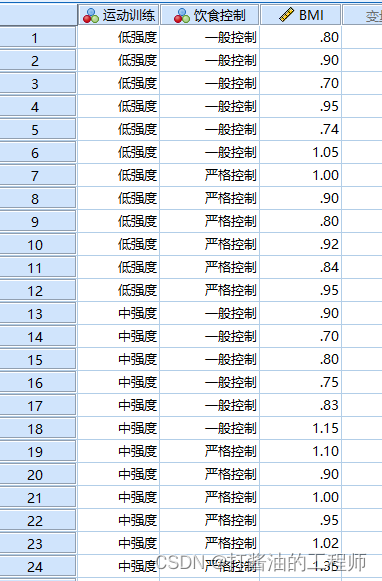
现将36名肥胖大侠随机分配到这6种组合干预方案中，每个组合方案6人，1个月后测量他们的BMI值的减少量，获得数据如下表。
问: 运动训练和营养控制有无作用？两种方案有无交互作用？
读数据：

GET 
  FILE='E:\E盘备份\recent\小白爱上SPSS\小白数据\第九讲 两因素析因设计的方差分析.sav'. 

二、统计策略

统计分析策略口诀“目的引导设计，变量确定方法”
针对上述案例，扪心六问。
Q1：本案例研究目的是什么？
A：比较差异。
Q2：本案例属于什么研究设计？
A：实验设计，两因素析因设计
Q3：有几个变量？
A：有三个变量。
自变量1为运动干预，分三个水平：高、中等和低强度；
自变量2为饮食控制，分两个水平：一般控制和严格控制；
因变量为BMI值，连续型变量。
Q4：变量类型是什么？
A： 自变量1和自变量2均为分类变量。
BMI为连续型变量。
Q5：各组数据服从正态分布么？
A：需要检验。
若服从，采用两因素析因设计方差分析；
若不服从正态，目前尚未替代的非参数检验方法（这只是原作者观点，若您发现有替代方法，请回复，感谢！）。
原作者建议：①转换数据；②由于方差分析对数据正态性不是特别敏感，若数据不是那么严重偏态，仍然可以进行方差分析。
Q6：各组数据的方差齐性么？
A：需要检验。
若不满足齐性，SPSS也未给出替代方案（这只是原作者观点，若您发现有替代方法，请回复，感谢！）
原作者建议：①转换数据；②如果各组样本量一致、符合正态性并且方差最大组与最小组的比值小于3，那么即使方差不齐，也可尝试采用方差分析。
概括而言，如果数据满足以下条件，则采用两因素析因设计的方差分析。

三、SPSS操作

1、正态性检验

本案例需要对各组合进行正态性检验。
命令行：

EXAMINE VARIABLES=BMI BY  运动训练  BY 饮食控制
  /PLOT HISTOGRAM NPPLOT /*若无此行，则不输出正态性检验表*/
  /COMPARE GROUPS 
  /STATISTICS DESCRIPTIVES 
  /CINTERVAL 95 
  /MISSING LISTWISE 
  /NOTOTAL.

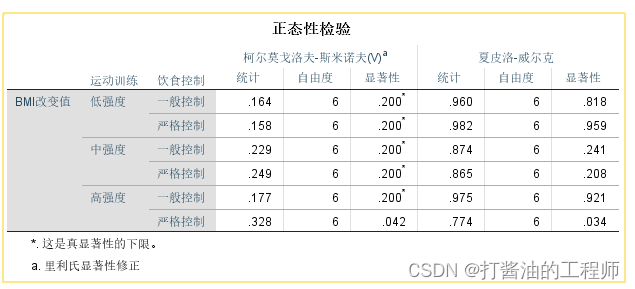
经S-W（夏皮洛-威尔克）检验，发现高强度-严格饮食控制这一组的p=0.034<0.05，有统计学意义，表明其不服从正态分布；而其他各组p均大于0.05，服从正态分布。
由于p=0.034, 比0.05稍微小点，我们对其宽容点，仍然采用方差分析。

2、方差分析

Step1：依次点击“分析——一般线性模型——单变量”。
Step2：在弹出的单变量对话框中，将“BMI”放入“因变量”框中，因考察的两因素均为分类变量，因此，将“运动训练”“饮食控制”均放入“固定因子”框中。
Step3：点击“模型”，出现“单变量：模型”对话框，默认选择“全因子”,，点击继续。全因子表明会输出运动训练主效应、饮食控制主效应、以及两者的交互效应。

Step4：点击“事后比较”，出现“多重比较”对话框。将“运动训练”“饮食控制”放入右边对话框，同时选择一种多重比较方法，比如“邦弗伦尼”。

Step5：点击“EM 平均值”，出现“估计边际平均值”对话框。将“运动训练”“饮食控制”和“运动训练*饮食控制”放入右边对话框，同时勾选“比较主效应”，再选择“邦弗伦尼”。
Step6：点击“选项”，出现“选项”对话框。主要勾选“描述统计”、“效应量估计”和“齐性检验”。
Step7：点击“继续”和“确定”，就能输出结果。
命令行：

UNIANOVA BMI BY 运动训练 饮食控制 
  /METHOD=SSTYPE(3) 
  /INTERCEPT=INCLUDE 
  /POSTHOC=运动训练 饮食控制(BONFERRONI) 
  /EMMEANS=TABLES(运动训练) COMPARE ADJ(BONFERRONI) 
  /EMMEANS=TABLES(饮食控制) COMPARE ADJ(BONFERRONI) 
  /EMMEANS=TABLES(运动训练*饮食控制) 
  /PRINT ETASQ DESCRIPTIVE HOMOGENEITY 
  /CRITERIA=ALPHA(.05) 
  /DESIGN=运动训练 饮食控制 运动训练*饮食控制.

四、结果解读

两因素析因设计方差分析的结果有多个表格，在此讲解几个重点表格。
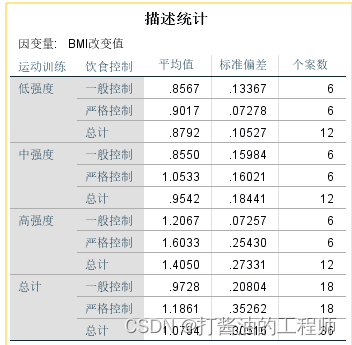
第一，描述性统计结果，包括平均数和标准差。

第二，Leven方差齐性检验结果。
可选择第一行基于平均数结果，结果显示方差齐性检验p=0.397，大于0.05，不具有统计意义，支持原假设，具有方差齐性，可采用F检验。

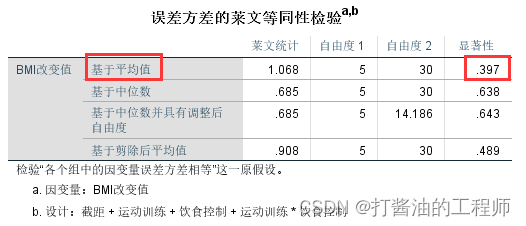
第三，主体间效应检验。
从表格中可知，运动训练的主效应显著，F=40.360，p<0.001，偏Eta平方=0.729; 饮食控制的主效应显著，F=17.03，p<0.001，偏Eta平方=0.362；更重要的是，运动训练与饮食控制的交互效应显著，F=3.877，p=0.032，偏Eta平方=0.205。
偏Eta平方是指效应量，数值越大，表明效应量越大，现在越来越多的杂志要求报告效应量。

Tips：效应量越大越好吗？

引自百度经验：效应量越大越好吗
是的。
效应量是越大越好，一般来说Cohen’s d系数在0.2-0.5为小效应量，0.5-0.8为中等，0.8以上为大效应。不同的研究者有不同的划分方法。其他的可以参考Cohen’s d系数。
效应量是指由于因素引起的差别，是衡量处理效应大小的指标。与显著性检验不同，这些指标不受样本容量影响。它表示不同处理下的总体均值之间差异的大小，可以在不同研究之间进行比较。
平均值差异、方差分析解释比例、回归分析解释比例需要用效应量描述。效应量不受样本容量的影响。当样本容量大得到显著时，有必要报告效应量大小。
一般用于针对某一研究领域内的元分析中，经常见于心理，教育，行为研究等。其主要统计思路是指主要变量引起的效应差别除以相应的标准误差，这一相对量对估算处理效应很重要。
效应量太小，意味着处理即使达到了显著水平，也缺乏实用价值。

统计分析策略

针对两因素方差分析，再次强调统计分析策略。
(1) 如果自变量之间不存在交互作用，进行主效应分析；
(2) 如果自变量之间存在交互作用，进行简单主效应分析，而主效应不是那么重要了。
本案例交互效应显著，故着重分析交互效应和简单效应。
第四，成对比较和多重比较。
主要呈现运动训练的三个水平之间两两比较；以及饮食控制的两个水平比较。



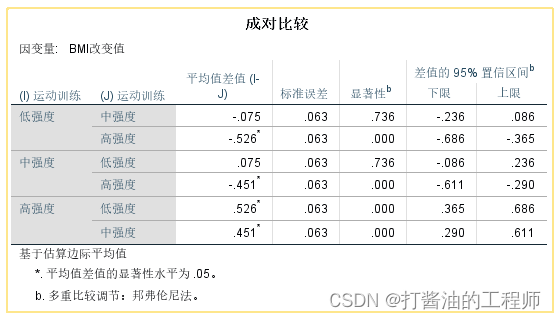
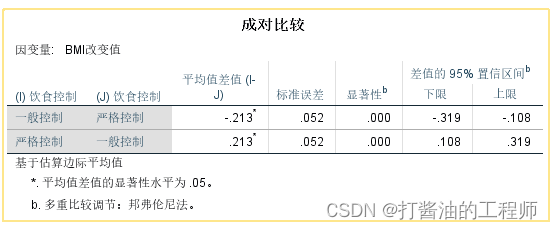
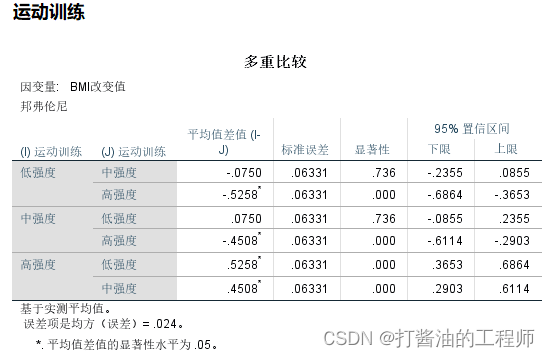
这几个表格与之前《第七讲 | 单因素方差分析怎么做？》的事后多重比较类似。
稍微说明一下，运动训练有三个水平，会呈现多重比较结果；但饮食控制只有两个水平，故没有多重比较结果。
接下来重点分析交互效应和简单效应。

五、简单效应操作及结果

1、SPSS操作

Step1：分析-一般线性模型-单变量，回到上述“单变量”窗口，点击“粘贴”。
Step2：弹出IBM SPSS Statistics 语法编辑器界面，这里呈现的是之前所有菜单式操作的计算机语言。
Step3：在/EMMEANS=TABLES(运动训练饮食控制)，按【回车键】，另起一行，输入或者复制粘贴以下语句。
/EMMEANS=TABLES(运动训练饮食控制)COMPARE(运动训练)ADJ(BONFERRONI)
/EMMEANS=TABLES(运动训练*饮食控制)COMPARE(饮食控制)ADJ(BONFERRONI)
完整命令行：

UNIANOVA BMI BY 运动训练 饮食控制
  /METHOD=SSTYPE(3)
  /INTERCEPT=INCLUDE
  /POSTHOC=运动训练 饮食控制(BONFERRONI) 
  /EMMEANS=TABLES(运动训练) COMPARE ADJ(BONFERRONI)
  /EMMEANS=TABLES(饮食控制) COMPARE ADJ(BONFERRONI)
  /EMMEANS=TABLES(运动训练*饮食控制) 
  /EMMEANS=TABLES(运动训练*饮食控制)COMPARE(运动训练)ADJ(BONFERRONI)
  /EMMEANS=TABLES(运动训练*饮食控制)COMPARE(饮食控制)ADJ(BONFERRONI)
  /PRINT ETASQ DESCRIPTIVE HOMOGENEITY
  /CRITERIA=ALPHA(.05)
  /DESIGN=运动训练 饮食控制 运动训练*饮食控制.

如下图：

解释：TABLES(运动训练*饮食控制)指的是“运动训练”与“饮食控制”的交互效应；
COMPARE(运动训练)是指根据“运动训练”变量提供简单主效应结果，就是固定饮食控制某一个水平，比较运动训练三个水平之差异，需采用多重比较。
ADJ(BONFERRONI) 多重比较的调整方法，一般选择LSD、Bonferroni、SIDAK调整。本案例选择Bonferroni调整。
Step4：点击“运行”——“全部”。即可呈现简单效应结果。

2、结果解读

第一张，运动训练的简单效应。

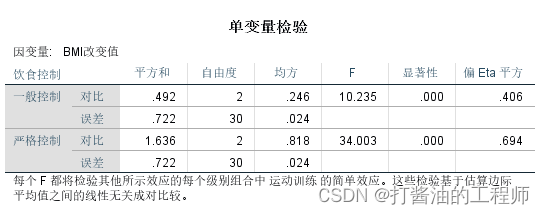
结果显示，在一般饮食控制下，运动训练的简单效应显著，F=10.235，p<0.001, 偏η2=0.406;
在严格饮食控制下，运动训练的简单效应显著，F=34.003，p<0.001, 偏η2=0.694;
由于运动训练有三个水平，到底哪两两之间有显著性差异呢？
我们要查看成对比较。
第二张，运动训练三水平的成对比较结果

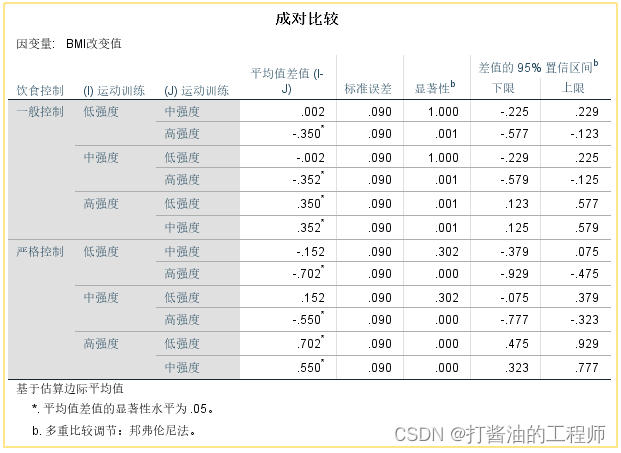
该成对比较结果显示：
在一般饮食控制下，低强度和中强度的BMI减少量之间无显著性差异（p=1.00>0.05，不具有统计学意义，支持原假设）；在严格饮食控制下，低强度与中强度的BMI减少量之间无显著性差异(p=0.302)；
而无论是一般饮食控制，还是严格饮食控制条件下，高强度与中强度、高强度与低强度两两比较均有显著性差异（p<0.001）。
这一结果似乎没有很好地体现交互效应，不急，我们再看看饮食控制的简单效应。
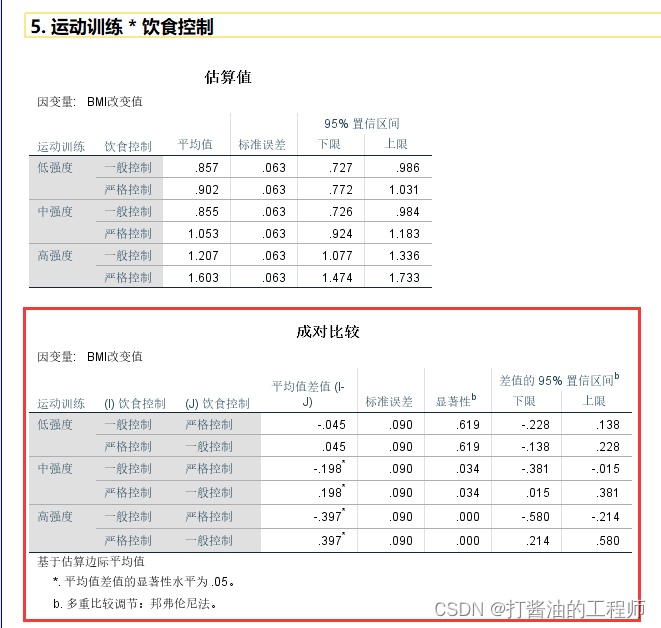
第三张，饮食控制的简单效应

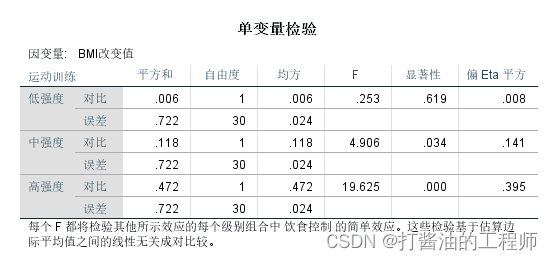
结果显示：
在低强度下，饮食控制的简单效应不显著，F=0.253，p=0.619, 偏η平方=0.008;
在中强度下，饮食控制的简单效应显著，F=4.906，p=0.034, 偏η平方=0.141;
在高强度下，饮食控制的简单效应显著，F=19.625，p<0.001 偏η平方=0.395。
非常好，该结果能较好地反映出了交互作用，也就是说饮食控制的干预效果会随着运动强度水平发生变化。
只有在中和高强度运动条件下，饮食控制才有效果；而在低强度运动条件下，饮食控制无效。
第四张， 饮食控制的成对比较，由于饮食控制只有两个水平，虽然我们选择了Bonferroni矫正，实际上并没有多重比较和矫正。
仔细对比发现，成对比较结果的p值与第三张表格简单效应p值是一模一样的。

六、规范报告

规范报告有多种方式，本公众号只提供一种方式供参考。

1、规范表格

饮食控制与运动干预对BMI减少量的方差分析结果

2、规范文字

方差分析结果显示：
运动训练的主效应显著，F=40.36，p<0.001，偏η2=0.73;
饮食控制的主效应显著，F=17.03，p<0.001，偏η2=0.36；
运动训练与饮食控制的交互效应显著，F=3.88，p=0.032，偏η2=0.21。
进一步检验效应结果显示：
在低强度下，饮食控制的简单效应不显著，F=0.24，p=0.62, 偏η2=0.01;
在中强度下，饮食控制的简单效应显著，F=4.91，p=0.03, 偏η2=0.14;
在高强度下，饮食控制的简单效应显著，F=19.63，p<0.001 偏η2=0.40。
小白学了两因素析因设计的方差分析，感觉有些吃力，但很充实。
他躺在床上思考，两个因素中，如果有一个因素是重复测量（比如前测，中测和后测）；另一个是组间设计，比如实验组和对照组，这时应该怎么分析？
想着想着，无法入睡，干脆起床，查了查，下一节内容：两因素重复测量方差分析。

划重点

1、析因设计是将两个或多个因素的各水平交叉分组，对各组合都进行实验的一种设计。

2、两因素析因设计方差分析策略是：两个分类自变量，一个连续型因变量；自变量分成两个或两个以上水平；各组数据需满足正态性和方差齐性（该条件可适当放宽）。

3、两因素析因设计方差分析主要分析两个因素的主效应，两个因素的交互效应，以及对应的简单效应。

4、如果两自变量之间不存在交互效应，则着重分析主效应；如果存在交互效应，着重分析交互效应和简单主效应，而主效应不是那么重要了。