📖 前言：长期以来，图像识别技术一直是人工智能研究领域的难题。近年来，随着算力的提升、物联网与大数据的出现、机器学习算法的快速发展，科学家们终于找到了有效的方法来实现图像识别，这就是基于人工神经网络的深度学习。很多以人工智能技术应用为主要发展目标的公司，如百度、阿里巴巴、腾讯和微软等，都推出了基于深度学习算法的图像搜索引擎，为人们的生产和生活提供了便利。

在这里插入图片描述

🕒 1. 深度学习发展简史
🕒 2. 多层感知器
- 🕘 2.1 人工神经网络（ANN）
- 🕘 2.2 基本原理
- 🕘 2.3 全连接前馈网络
- 🕘 2.4 输出层（多类分类器）
- 🕘 2.5 手写数字识别（原理分析）
🕒 3. 综合案例：手写数字识别
🕒 4. 深度学习技巧
- 🕘 4.1 过拟合
- - 🕤 4.1.1 引入正则化项
  - 🕤 4.1.2 Dropout
  - 🕤 4.1.3 提前终止训练
  - 🕤 4.1.4 增加样本量
- 🕘 4.2 欠拟合
- - 🕤 4.2.1 调节学习率
- 🕘 4.3 参数不合适
- - 🕤 4.3.1 新的激活函数
🕒 5. 课后习题

🕒 1. 深度学习发展简史

在这里插入图片描述

1943年，麦卡洛克(Warren McCullock)和皮兹(Walter Pitts)提出第一个脑神经元的抽象模型
1958年，罗姆布拉特(Frank Rossenblatt)基于MCP神经元模型提出第一个感知器学习算法
1969年，明斯基(Marvin Minsky)和Seymour Papert出版了《Perceptron》一书，分析了感知器模型的局限性
1986年，D.E. Rumerlhart，辛顿(G.E. Hinton)和R.J. Williams发表论文，阐释并推广了反向传播算法（Back Propagation, BP）
2006年，Hinton等人提出一种可以实现快速学习的深度信念网络（DBN）
2009年，GPU被用于训练深度神经网络
2012年，AlexNet在ImageNet图像识别竞赛中达到83.6%的Top5精度
2015年，微软的ResNet以96.43%的Top5精度，超过人类水平（94.9%）
2016年，AlphaGo击败围棋世界冠军Lee Sedol
2017年，AlphaGo Zero以100:0击败AlphaGo
2017年，IBM将语音识别错误率降到5.5%（人类5.1%）

小结：感知器：本质上是线性模型
多层感知器+BP：解决非线性分类，存在梯度消失问题

🕒 2. 多层感知器

🕘 2.1 人工神经网络（ANN）

当前，新一代人工智能领域中最重要研究内容之一就是基于人工神经网络的深度学习。人工神经网络（Artificial Neural Network，ANN）是相对生物神经网络（Biological Neural Network，BNN）而言的，受生物神经网络的启发而生。生物神经网络最基本的结构和功能单位是神经元（Neuron）。神经元的树突较短且分支多，其作用是接收其他细胞传递过来的电信号；轴突则较长且分支少，用于将电信号传递给其他细胞，如图所示。成千上万个神经元相互连接，共同组成复杂的生物神经网络。人类大脑皮层中约有140多亿个神经元，在接收外部信号过程中，脑细胞会不断地调整神经元的兴奋阈值，宏观上表现为学习、思考和判断等高级思维活动。

在这里插入图片描述

🕘 2.2 基本原理

在这里插入图片描述

M - P神经元模型是按照生物神经元的结构和工作原理构造出来的一个抽象和简化的计算模型，如图所示，神经元接收来自n个其他神经元传递过来的输入信号 $x_1，x_2，...，x_n$ ，这些输入数据通过加权计算之后，神经元将会判断其是否超过神经元阈值 $\theta$ 。如果超过阈值，神经元将被激活，并通过“激活函数（activation function） $f$ ”产生神经元的输出。其中各神经元有不同的阈值 $\theta$ （即包含了权重（weights）和偏置（bias））。

理想中的激活函数是图(a)所示的阶跃函数，它将输入值映射为输出值“0”或“1”，显然“1”对应于神经元兴奋，“0”对应于神经元抑制。然而，阶跃函数具有不连续、不光滑等不太好的性质，因此实际常用Sigmoid函数作为激活函数。典型的Sigmoid函数如图(b)所示，它把可能在较大范围内变化的输入值挤压到(0,1)输出值范围内，因此有时也称为“挤压函数”(squashing function)。

在这里插入图片描述

常用激活函数及其函数图像
在这里插入图片描述

以Sigmoid函数为例，构造模型
在这里插入图片描述
这就是只有一层的人工神经元模型，也称为单个感知器。输入层被称为第零层，因为它只是缓冲输入。存在的唯一一层神经元形成输出层。
下图是多个感知器（多层人工神经网络）

在这里插入图片描述

多层感知器（即多层人工神经网络）在感知器的基础上，增加了若干隐藏层，通过前向传播算法将输入信息进行前向传播，在学习过程中利用反向传播学习算法将误差进行前向传播，以调整每一层的连接参数。下图所示的是具有一层隐藏层的多层感知器，感知器每层中所有的神经元都与上层所有神经元相连。这种连接方式也称为全连接人工神经网络。
在这里插入图片描述

🕘 2.3 全连接前馈网络

所谓前馈网络就是前向传播，如上图 $h_1$ 神经元的输入来自
于 $i_1、i_2、i_3、i_4$ 的输出，其本身的输出又可继续传递给 $\sigma_1$ 和 $\sigma_2$ 。

以下是前面Sigmoid函数的全连接前馈网络，看起来有点像前面集成学习的“提升”技术。

在这里插入图片描述
给定网络结构，就定义了一组函数

在这里插入图片描述
构造多层隐藏层的多层感知器，深度就是多个隐藏层

在这里插入图片描述

🕘 2.4 输出层（多类分类器）

在这里插入图片描述

特征抽取（隐藏层）替代了特征工程
softmax层：对神经网络的输出结果进行了一次换算，将输出结果用概率的形式表现出来。

$\operatorname{Softmax}\left(z_{i}\right)=\frac{e^{z_{i}}}{\sum_{c=1}^{C} e^{z_{c}}}$

🕘 2.5 手写数字识别（原理分析）

在这里插入图片描述

你需要构建一个神经网络结构以包含一个好的可用于手写数字识别的函数。

训练数据：准备训练数据（图像及其标签），学习目标定义在训练数据之上

在这里插入图片描述
学习目标：

损失函数可以是网络输出值与目标值之间的平均差（回归任务）或交叉熵（分类任务）

整体损失（尽可能小）：
$L=\sum_{r=1}^{R} l_{r}$

在这里插入图片描述

在函数集中找到使整体损失L最小的一个函数，找到能最小化整体损失L的一组网络参数 $\theta ^∗$

枚举（不使用）
梯度下降法

选取一个初始的 $\omega$ 值，计算 $\frac{\partial L}{\partial \omega}$
负数就增大 $\omega$ ，正数就减小 $\omega$
$\leftarrow w-\eta（学习速率） \partial L / \partial w$

在这里插入图片描述

重复上面公式，直至 $\frac{\partial L}{\partial \omega}$ 很小（几乎无变化）

在这里插入图片描述

但是这样会有问题，就是无法找到全局的极小值点

在这里插入图片描述

上面这个图像是二维的，我们转为三维看看
在这里插入图片描述
同样会存在问题，不同的起点会到达不同的极小值点，即不同的结果。

基于梯度下降有一个高效算法：反向传播算法（Backpropagation）
在这里插入图片描述

许多已有的深度学习框架可以自动计算梯度。

🔎 反向传播算法介绍

🕒 3. 综合案例：手写数字识别

为了训练机器识别手写数字，机器学习领域最知名的学者之一 Yann Le-Cunn利用美国国家标准与技术研究院（National Institute of Standards and Technolo-gy，NIST）的手写数字库构建了一个便于机器学习研究的集合MNIST。该数据集由70 000张不同人书写的数字（0~9）灰度图组成，每张图片的大小是28×28像素，数字的大小是20×20，位于图片的中心。其中 60 000张是训练集，另外10 000张是测试集。

🔎 MNIST数据集

因为数字只有0~9一共10个，对于任意一张图片，仅需要确定它是0～9中间的哪个数字，所以这是一个多分类问题。对于原始图片，可以将其看作一个28×28的矩阵，作为机器学习模型的输入，实际使用时一般将其展开成784维的一维数组。

在这里插入图片描述

本节采用高级神经网络API库 Keras构建多层感知机模型对手写数字进行多分类建模。大概分为如下几步：

🔎 Keras数据集
读入数据

from keras.datasets import mnist
# Keras提供了数据集加载函数
from keras.utils import np_utils  
from keras.models import Sequential  
from keras.layers import Dense, Activation

print(X_train.shape)		# (60000, 28, 28)
print(X_test.shape)			# (10000, 28, 28)
print(y_train.shape)		# (60000,)
print(y_test.shape)			# (10000,)

数据预处理

# 采用reshape 函数将每个图像矩阵扁平化成一个向量
X_train = X_train.reshape(X_train.shape[0], X_train.shape[1]*X_train.shape[2])
X_test = X_test.reshape(X_test.shape[0], X_test.shape[1]*X_test.shape[2])
print(X_train.shape)
print(X_test.shape)
# 将输入值从[0，255]归一化为[0，1]的值
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
# 调用to_categorical函数将每个类别值转换成一个10维的0/1向量
Y_train = np_utils.to_categorical(y_train, 10)
Y_test = np_utils.to_categorical(y_test, 10)

构建一个三层的神经网络
在这里插入图片描述

model = Sequential() 		# 初始化一个序列模型
# 添加输入为784维，输出为500维，激活函数为sigmoid 的一层神经网络
model.add(Dense(500, input_dim=784))		
model.add(Activation('sigmoid'))
# 在上一层神经网络上，继续添加输出为500维，激活函数为sigmoid的一层神经网络:
model.add(Dense(500))
model.add(Activation('sigmoid'))
# 最后一层为输出层，输出的维度为10，激活函数为softmax函数
model.add(Dense(10))
model.add(Activation('softmax'))
model.summary()			# 打印模型概况

在这里插入图片描述
确定学习目标

model.compile(loss = 'mean_squared_error', 		# compile函数设置了学习的目标
			optimizer = 'sgd', 
			metrics = ['accuracy'])

loss：损失函数，该例子中采用的是mean_squared_error，优化的目标是真实值与预测值之间差距平方和的平均值，
- 更多：🔎 Keras数据集。
optimizer：优化算法，该例子中采用的 sgd，即随机梯度下降法，其基本思想是用样本中的一个例子来近似所有的样本，调整模型参数。
- 更多：🔎 Keras数据集。
metrics：评价指标，该例子中采用的是accuracy，即准确率，
- 更多：🔎 Keras数据集.

模型学习

model.fit(X_train, Y_train, batch_size=100, epochs=20)
# X_train是训练数据（图像），Y_train是类别标签（数字）

batch_size：每次批量抽取的样本数量。batch_size太小，例如只有一个样本，则梯度每遇见一个样本就更新一次，会导致可能达不到全局最优解；batch_size太大，例如全部样本，则梯度要在遍历完所有样本才更新一次，会导致收敛速度非常慢。因此，常用的方法是做小批量更新（Mini-batch），即每次取一定数量的样本来更新模型。
epochs：遍历整个数据集的遍数，一般要遍历几十遍才可能达到收敛的效果。

模型评估

score = model.evaluate(X_test, Y_test)
print('Test loss: ', score[0])		# 第一维是模型的损失值
print('Test accuracy: ', score[1])		# 第二维是模型评估的精度

10000/10000 [==============================] - 1s 88us/step
Test loss: 0.089208979845047
Test accuracy: 0.1526

模型的使用

result = model.predict(X_test)

在这里插入图片描述

🕒 4. 深度学习技巧

🕘 4.1 过拟合

多层神经网络参数很多，具有强大的表示能力，但是容易产生过拟合现象。即模型连训练集的一些最细微的特征都记住了，因此泛化能力有限，在未知数据上的预测能力很差。而机器学习的目标就是让模型在测试集上也拥有很强的表示能力，不仅局限于拟合训练数据。神经网络中常见的避免过拟合的方法包括引入正则化项、Dropout、提前终止训练以及增加样本量等。

🕤 4.1.1 引入正则化项

给需要训练的损失函数加上一些规则限制，让优化得到的参数不要过大。具体来讲，正则化的方法会保留所有的模型参数，使每一个模型参数都对预测产生一点影响，但会将一些不重要的特征对应的参数置为很小的数甚至为0，使得特征的参数矩阵变得稀疏。

常见正则化有L1正则化和L2正则化

🕤 4.1.2 Dropout

在这里插入图片描述
训练时：
每次修改参数值前，每个神经元有p%的概率退出，网络结构改变，训练新的网络

对每个mini-batch, 我们重新随机选取退出的神经元

测试阶段仍然是原来的网络结构

没有Dropout

如果训练时的退出概率是p%, 则所有的权重都乘以（1-p%）
假设退出概率是50%，如果一个权重w训练得到的值是1，则测试时将𝑤的值设为0.5

直观理解：平时跑步的时候脚上绑沙袋，体测的时候去掉沙袋就会感觉很轻松。

为什么测试时网络的权重应该乘以(1-p)% (dropout rate)?
在这里插入图片描述
Dropout也是一种集成学习

🕤 4.1.3 提前终止训练

在这里插入图片描述

🕤 4.1.4 增加样本量

增加样本量可以减轻过拟合的风险。因为过拟合本质上就是模型对数据分布的学习过头了，以至于记住了数据的点点滴滴，这样过分的记忆导致模型在测试集上的表现变得很差。增加样本量使得模型记住数据全部细节变得非常困难。在实际应用中，虽然上述几种技术方法对防止过拟合都很有效，但增加样本量确实能够更加直接地避免过拟合。

🕘 4.2 欠拟合

当发现模型在训练集上的损失始终很大，无法下降，说明模型的拟合能力有限。一般的做法是增加模型的复杂度，例如，加大神经网络的层数或每层神经元的个数。一般来说，在计算能力范围内，模型参数量越大，如越深或越广，则拟合能力越强。

🕤 4.2.1 调节学习率

学习过程中的学习率一般设为可动态调节的，而非固定不变的。一般训练的初始阶段需要从随机参数开始大幅度调整模型的参数，以加快收敛的速度，因此需要采用较大的学习率;之后随着训练次数的增加，模型已经达到一定的效果，此时需要一个较小的学习率对模型进行微调，使得模型达到一个比较高的准确度。因此学习率可以设置为随着训练次数以一定的比率呈指数下降的变量。

🕘 4.3 参数不合适

🕤 4.3.1 新的激活函数

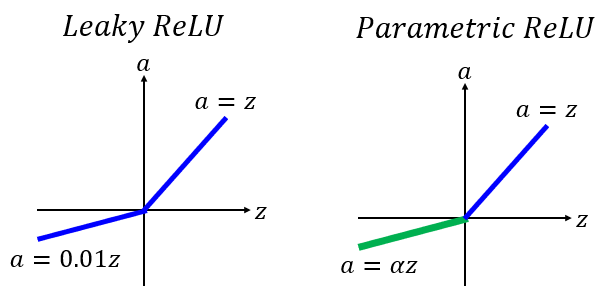
线性整流函数:Rectified Linear Unit (ReLU)
在这里插入图片描述

原因：

快速计算
符合生物神经元特征
Infinite sigmoid with different biases

更多：🔎 激活函数文档

在这里插入图片描述

变式
α 也用梯度下降法学习

在这里插入图片描述
当使用softmax输出层时，使用交叉熵损失函数

🕒 5. 课后习题

【单选题】感知机模型和( )工作机制相同，模型的函数表示形式类似。
A. 线性逻辑回归模型
B. 支持向量机模型
C. 决策树模型
D. 朴素贝叶斯模型
【单选题】用于多分类问题的深度神经网络选择( )作为其输出层激活函数比较合理。
A. Sigmoid函数
B. 阶跃函数
C. ReLU函数
D. Softmax函数
【单选题】用于识别手写数字的深度神经网络选择( )作为其损失函数比较合理。
A. 均方误差
B. 交叉熵
C. 合页损失
D. 基尼指数
【单选题】基于M-P神经元的神经网络中，( )是使得神经网络具有非线性建模能力的关键。
A. 偏置
B. 求和函数
C. 激活函数
D. 输入权重
【多选题】为防止过拟合，在深度神经网络构建和训练时可采取哪些措施？
A. 引入正则化项
B. 使用Dropout技术
C. 提前终止训练
D. 增加样本量
E. 设置较小的学习率
【判断题】前馈神经网络的模型训练通常采用反向传播(BP, back propagated)算法进行参数调优，BP算法是一种梯度下降算法。