主要研究人体姿态估计中heatmap转坐标的方法，提出一种新的解码方法

（其实这人体姿态我毛也不会，过来看看这个heatmap解码方法）
代码：https://github.com/ilovepose/DarkPose/blob/master/lib/core/inference.py

方法

人体姿态估计简单来说就是要预测人的所有关节的坐标，这里主要研究把关节转为热体图，然后进行回归的那种方法。

根据上下文推测，这里应该是一个关键点一个通道heatmap

Coordinate Decoding

如果输出的heatmap的尺寸和原图的大小一样，那么我们只需要找到最大的点。
然而通常我们输出的heatmap需要上采样到原来的尺寸，也就是乘以一个系数$\lambda \in {\mathbb{R}}_{++}$
这将导致亚像素定位问题（sub-pixel localisation)

The standard coordinate decoding method

令$\mathbf{h}$为模型输出的heatmap
heatmap最大值$\mathbf{m}$，第二大值$\mathbf{s}$
那么heatmap中的关节位置
$$\mathbf{p}=\mathbf{m}+\frac{1}{4}\frac{\mathbf{s}-\mathbf{m}}{\Vert \mathbf{s}-\mathbf{m}{\Vert }_2}$$
这个就是最大值往第二大值的方向移动$\frac{1}{4}$像素

最终原图像的关节位置为
$$\hat{\mathbf{p}}=\lambda \mathbf{p}$$

这个移动的主要目的是补偿下采样导致的量化效应
heatmap中最大值点并不代表真实关节的位置，只是一个大概的位置。

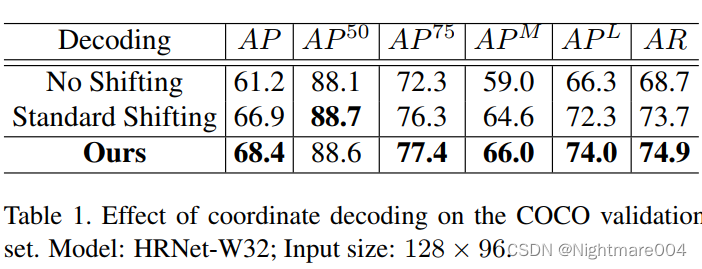
从这个表可以看出，这个移动能够带来很大的提升

Our coordinate decoding method

我们假设预测出来的heatmap和生成的heatmap服从高斯分布
因此预测的heatmap
$$\mathcal{G}\left(\mathbf{x};\mu ,\mathbf{\Sigma }\right)=\frac{1}{\left(2\pi \right){\left|\mathbf{\Sigma }\right|}^{\frac{1}{2}}}\exp \left(-\frac{1}{2}{\left(\mathbf{x}-\mu \right)}^{\mathrm{T}}{\mathbf{\Sigma }}^{-1}\left(\mathbf{x}-\mu \right)\right)$$
其中$\mathbf{x}$是预测heatmap中的像素坐标，
$\mu$是高斯中心，也就是预测的关节位置
$\mathbf{\Sigma }$是协方差矩阵，是一个对角矩阵
$$\mathbf{\Sigma }=\left[\begin{array}{cc}{\sigma }^2& 0\\ 0& {\sigma }^2\end{array}\right]$$
$\sigma$是标准差

取个对数
$$\begin{array}{rl}\mathcal{P}\left(\mathbf{x};\mu ,\mathbf{\Sigma }\right)& =\ln \left(\mathbf{G}\right)\\ & =-\ln \left(2\pi \right)-\frac{1}{2}\ln \left(\left|\mathbf{\Sigma }\right|\right)-\frac{1}{2}{\left(\mathbf{x}-\mu \right)}^T\end{array}$$
一阶导
$${{\mathcal{D}}^{\prime }(\mathbf{x})|}_{\mathbf{x}=\mathbf{\mu }}={\frac{\partial {\mathcal{P}}^T}{\partial \mathbf{x}}|}_{\mathbf{x}=\mathbf{\mu }}=-{{\Sigma }^{-1}(\mathbf{x}-\mathbf{\mu })|}_{\mathbf{x}=\mathbf{\mu }}=0$$
二阶导
$${\mathcal{D}}^{\prime \prime }(\mathbf{m})={{\mathcal{D}}^{\prime \prime }(\mathbf{x})|}_{\mathbf{x}=\mathbf{m}}=-{\Sigma }^{-1}$$
在最大值点泰勒展开到二阶
$$\mathcal{P}(\mathbf{\mu })=\mathcal{P}(\mathbf{m})+{\mathcal{D}}^{\prime }(\mathbf{m}{)}^T(\mathbf{\mu }-\mathbf{m})+\frac{1}{2}(\mathbf{\mu }-\mathbf{m}{)}^T{\mathcal{D}}^{\prime \prime }(\mathbf{m})(\mathbf{\mu }-\mathbf{m})$$
接着就能得到
$$\mathbf{\mu }=\mathbf{m}-{\left({\mathcal{D}}^{\prime \prime }(\mathbf{m})\right)}^{-1}{\mathcal{D}}^{\prime }(\mathbf{m})$$
说实话，不知道这个怎么得到的，我猜测是泰勒展开后求导为0得到的

代码里，一阶导和二阶导是用数字图像处理那种求导方法得到的

Heatmap distribution modulation

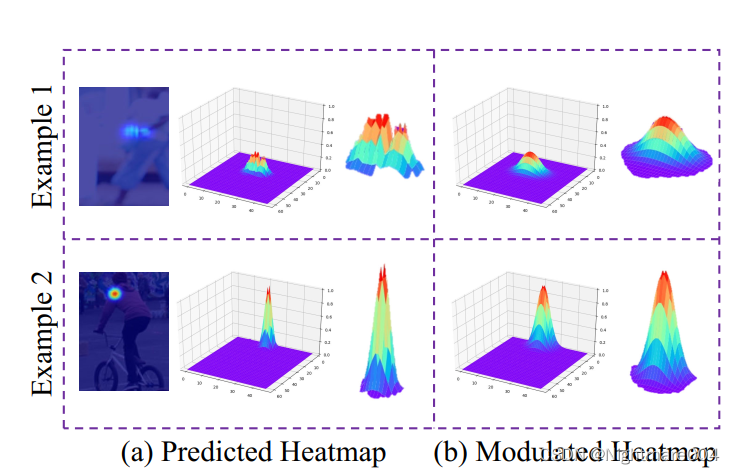
这个图(a)里是预测的heatmap，可以看出其实是有多个峰值的
这可能会对作者的解码方法产生负面影响。为了解决这个问题，先调整一下这个heatmap的分布

更具体地，为了解决这种多个峰值的情况，作者使用了和训练时方差一样的高斯核$\mathbf{K}$
$${\mathbf{h}}^{\prime }=\mathbf{K}⊛\mathbf{h}$$

为了保留原来的heatmap的大小（？magnitude），最终会放缩一下
$${\mathbf{h}}^{\prime }=\frac{{\mathbf{h}}^{\prime }-\min \left({\mathbf{h}}^{\prime }\right)}{\max \left({\mathbf{h}}^{\prime }\right)-\min \left({\mathbf{h}}^{\prime }\right)}\ast \max (\mathbf{h})$$

Coordinate Encoding

这里是讲热力图编码的方法

简单来说就是生成的时候不要用取整的方法得到热力图中心，而是直接生成